Метод динамического программирования инвестиций

Оптимальное распределение инвестиций методом динамического программирования

Динамическое программирование (ДП) — метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Начало развития ДП относится к 50-м годам XX в. Оно связано с именем Р.Беллмана.

Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели ДП применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т. п.

В реально функционирующих больших экономических системах еженедельно требуется принимать микроэкономические решения. Модели ДП ценны тем, что позволяют на основе стандартного подхода с использованием при минимальном вмешательстве человека принимать такие решения. И если каждое взятое в отдельности такое решение малосущественно, то в совокупности эти решения могут оказать большое влияние на прибыль.

Рассматривается управляемый процесс, например, экономический процесс распределения средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования, пополнения запасов и т. п.

В результате управления система (объект управления) S переводится из начального состояния (So), в конечное состояние (Sn). Предположим, что управление можно разбить на n-шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему S из начального состояния в конечное, представляет собой n-шаговый процесс управления.

Условие отсутствия последействия. Состояние S_k, в которое перешла система за один K- ый шаг, зависит только от состояния S_k-1 и выбранного управления x_k , и не зависит от того, каким образом система пришла в состояние Sk1:

Также учитывается, что выбор управления на k-ом шаге зависит только от состояния системы к этому шагу:

На каждом шаге управления x_k зависит от конечного числа управляющих переменных. Состояние системы на каждом шаге зависит от конечного числа параметров.

Принцип оптимальности. Каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. Основное требование, при котором принцип верен — процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.

Таким образом, решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.

Рекуррентные соотношения Беллмана.

Нахождение оптимального решения управляемого процесса можно произвести на основе рекуррентных соотношений Беллмана. Пусть f_k (S_k-1,x_k) — показатель эффективности k – ого шага при всевозможных управлениях . Выделяют обратную и прямую схемы Беллмана.

Таблица 6. Значения прибыли предприятий

Источник

Динамическое программирование. Задача о распределении инвестиций — видеоурок с решением задачи в Excel

>Ниже приведено условие задачи и текстовая часть решения. Закачка полного решения, файлы doc и xls в архиве zip, начнется автоматически через 10 секунд. Видеоурок по решению этих задач — внизу страницы.

Указать оптимальные размеры и потоки инвестирования, если прибыль от вложений (Х i ) в проекты (А i ) распределилась следующим образом:

Теперь для решения этой задачи воспользуемся Excel .

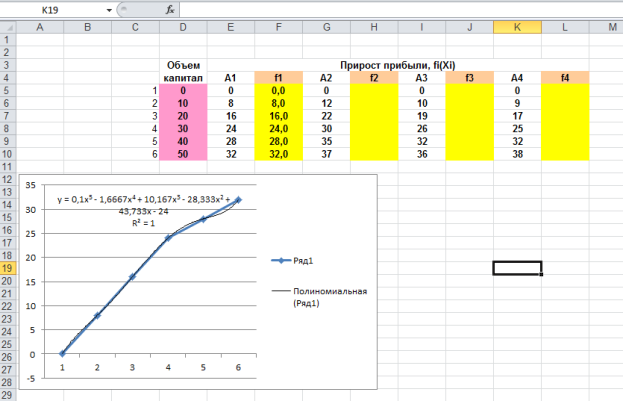
Для этого выделим шаги тренда t i , вложения x i и прибыли A i . Затем для каждого из четырех проектов построим средствами MS Excel графическую зависимость прибыли А от шага тренда ( t = 1, 2, 3, 4, 5 , 6 ). Активизируем точки графика, щелкнув по ним левой клавишей мыши, затем нажмем правую клавишу и выберем режим «Добавить линию тренда» . Для всех четырех проектов наилучшим типом является полиномиальный 5 -о й степени. С помощью полученных уравнений трендов находим теоретические значения прибыли при различных значениях шага тренда t i . Уравнения моделей тренда, коэффициенты аппроксимации и теоретические значения при были, представлены на рисунке 1.

Рис. 1. Графические зависимости прибыли от вложений и полиномиальные тренды этих зависимостей.

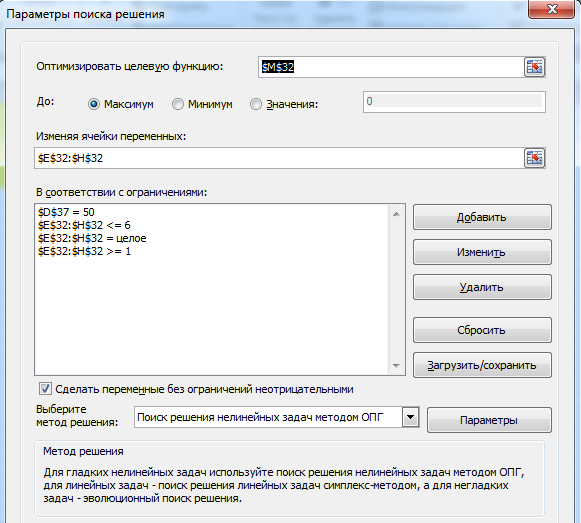
В ячейку М32 вводим выражение для общей (суммарной) прибыли, которую надо максимизировать, — это сумма всех четырех полиномиальных функций. Зависимыми переменными в этой функции являются искомые значения шагов тренда, которые будут располагаться в ячейках E 32 — H 32 . Суммарные вложения не должны превышать 5 0 тыс. ед., следовательно, вводим ограничение 1 0 *(E32+F32+G32 +H32 -4) в ячейку D 37 .

Выбираем из главного меню MS Excel режим «Поиск решения» и заполним открывшееся диалоговое окно в соответствии с требованиями. Нажмем клавишу «выполнить» и получим результат оптимизации.

Рис. 2. Модель максимизации прибыли.

Рис. 3. Оптимальное распределение капиталовложений между проектами.

Имя файла: dinprogr.zip

Размер файла: 129.98 Kb

Если закачивание файла не начнется через 10 сек, кликните по этой ссылке

Источник

Задачи динамического программирования

Данный раздел представлен следующими калькуляторами:

1. Задача распределения инвестиций. Распределении инвестиций между предприятиями П₁, П₂. П_n. Инвестируемая сумма E усл. ден. ед.
2. Задача распределения ресурсов. Планируется работа двух предприятий на n лет. Начальные ресурсы равны s₀ .
3. Метод прогонки.
4. Задача замены оборудования.
5. Складская задача: составить оптимальную программу выпуска продукции X , которая минимизирует суммарные издержки предприятия.
6. Задача Джонсона.
7. Задача о рюкзаке (решение задачи о загрузке транспортного средства).
8. Динамическая оптимизация в планировании работ
   В условиях задачи производственного планирования найти оптимальные сроки начала строительства каждого из объектов так, чтобы суммарный срок строительства всех объектов был бы минимальным.
   

   Объекты / Стадии	№1	№2	№3	№4
   A1	2	5	4	3
   A2	1	4	2	6
   A3	3	4	3	4

Задача распределения инвестиций

Таблицы могут иметь разный вид.
Таблица 1 — Первый вариант таблицы исходных данных

x	f1(x)	f2(x)	f3(x)
1	6.3	4	5
2	5.2	6	7
3	4.3	4.6	7.8
4	5	6	3
5*	7	6.3	8.2

* — здесь значение 5 — максимальное значение (сумма для распределения).

Таблица 2 — Второй вариант таблицы исходных данных

x	0	10	20	30	40
f1(x)	0	4	5	7	8
f2(x)	0	3	3	4	6
f3(x)	0	4	4	5	6

Пример задачи.
Для двух предприятий выделено A единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от x единиц средств, вложенных в первое предприятие, равен f₁(х), а доход от y единиц средств, вложенных во второе предприятие, равен f₂(y). Остаток средств к концу года составляет g₁(x) для первого предприятия и g₂(y) для второго предприятия. Задачу решить методом динамического программирования.

При вводе данных первую нулевую строку можно не заполнять.

В сервисе Задача распределения инвестиций используется метод обратной прогонки.

Метод прогонки

В сервисе Метод прогонки необходимо также выбрать метод решения: процедура прямой или обратной прогонки.

Источник

Метод динамического программирования инвестиций

Преподавание дисциплин экономико-математического цикла для студентов высших учебных заведений, обучающихся по экономическим специальностям, а также для студентов менеджериальных направлений подготовки, подразумевает изучение ряда прикладных вопросов математики, одним из которых является динамическое программирование. Методы динамического программирования базируются на принципе оптимальности Беллмана и при традиционной методике преподавания требуют выписывания рекуррентного соотношения Беллмана. Однако для данной категории студентов обучение должно быть ориентировано не столько на разъяснение прикладного значения преподавания математических дисциплин (как это имеет место в случае обучения студентов математических и педагогических направлений, для которых составлено большинство методических разработок по данной тематике), сколько на обучение решению вполне конкретных практических задач математическими методами. В связи с этим в процессе преподавания данного раздела студентам экономистам и менеджерам нецелесообразно применять сложную математическую терминологию, проводить громоздкие доказательства и обоснования, как это необходимо при обучении студентов-математиков, а требуется научить решать практические задачи возможно более короткими и доступными способами.

Целью настоящей работы является описание новой методики изложения темы «динамическое программирование», которая позволяет облегчить восприятие данной темы за счёт более компактного изложения и оформления решений и избегания излишней математической терминологии.

В процессе преподавания дисциплин «Исследование операций в экономике», «Методы принятия управленческих решений», «Экономико-математические методы и модели» у студентов, обучающихся на факультете экономики и управления ФГБОУ ВПО «Ульяновский государственный педагогический университет им. И.Н. Ульянова», автором разработан новый метод изложения темы «динамическое программирование». Этот метод позволяет сократить оформление решений практических задач. Рассмотренный алгоритм близок к изложенному в работе [4], однако имеет ряд отличий, например, он не включает в себя выписывания рекуррентных отношений Беллмана, не оперирует с понятием «остаток средств», а также некоторые другие. Был проведён педагогический эксперимент по сравнению результатов обучения данной теме согласно традиционной методике (базирующейся на учебных пособиях [1, 2, 3, 5] и др.) и по методике, описываемой ниже.

Разберём предлагаемую методику изучения темы «динамическое программирование» на примере определения оптимального плана инвестирования. Решим с помощью этого метода задачу, предложенную Л.И. Акуличем [2, № 4.2, 4.10.]. В задаче требуется составить оптимальный план инвестирования 700 тысяч рублей в три предприятия, максимизирующий итоговую суммарную прибыль, если доходность каждого предприятия в зависимости от объёмов капиталовложений задана табл. 1.

Прибыль, получаемая от предприятия в зависимости от объёма капиталовложений (тыс. руб.)

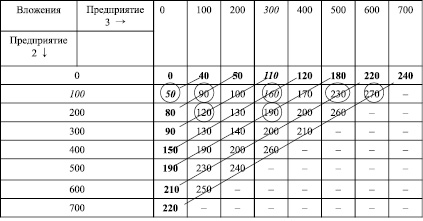
Решение. Традиционно решение задач линейного программирования начинается с разбивки решения на этапы. В данном случае, несмотря на единовременность принимаемого решения, можно выделить условные этапы – будем считать, что на первом этапе мы инвестируем средства в первое предприятие, на втором – во второе, на третьем – в третье. Хотя последовательность этапов в данном случае совершенно не существенна, опять следуя традиции, будем решать эту задачу методом обратной прогонки – то есть от последнего этапа к первому. Для выбора условно-оптимального управления на последнем шаге сделаем возможные предположения о состоянии системы (то есть об объёмах имеющихся у нас капиталов) к третьему этапу. Очевидно, что капитал, которым мы будем располагать к третьему этапу, будет находиться в пределах от 0 до 700 тыс. рублей. На последнем этапе (то есть в момент, когда решение по инвестированию в первое и второе предприятие уже принято), оптимальным управлением будет вложение всех оставшихся средств в третье предприятие (больше их просто некуда вложить). Доходы, получаемые от такого капиталовложения, занесём в две верхние строки табл. 2 (данные берутся из последнего столбца табл. 1). Далее таблицу заполняем следующим образом. В первом столбце таблицы укажем средства, предположительно вкладываемые во второе предприятие (начиная с 0; строку, которая начинается с 0, назовём нулевой). Заметим сразу, что если мы ничего не вложим в третье предприятие (столбец, вверху которого стоит 0; будем называть его нулевым столбцом), то доход будет получаться только от вложений во второе предприятие, поэтому в нулевой столбец копируем значения из столбца, соответствующего предприятию 2 в табл. 1. В остальных клетках укажем суммарную прибыль, которую можно получить от инвестирования соответствующих сумм во второе и третье предприятия одновременно (для этого складываем значения в нулевой строке и нулевом столбце табл. 2, которые выделены жирным шрифтом). Для сокращения пояснений обозначим каждую клетку парой чисел, первое из которых будет соответствовать количеству вкладываемых тысяч рублей, указанному в первом столбце таблицы, а второе – количеству тысяч рублей, указанному в верхней строке. Например, клетка (100, 300) – это клетка, в которую заносится доход от вложения 100 тыс. рублей во второе предприятие (доход составит 50 тысяч), в сумме с доходом от вложения 300 тыс. рублей в третье предприятие (доход 110 тысяч). Таким образом, суммарный доход от инвестирования этих средств составит 50 + 110 = 160 тыс. руб., поэтому в клетку (100, 300) заносится значение 160 (показано курсивом в табл. 2).

Прибыль от вложения средств во второе и третье предприятия

Клетки, сумма номеров которых больше 700, не заполняются (например, клетки (100, 700), (200, 600) и т.д.), поскольку эти клетки соответствуют суммарным инвестициям, превышающим 700 тысяч. Из данной таблицы легко видеть, что значения, соответствующие инвестициям конкретной денежной суммы, расположены по диагонали по отношению друг к другу. В этом случае сумма номеров клеток одинакова, например, возможные варианты инвестирования 300 тысяч находятся в клетках, сумма номеров которых равна 300 – это клетки (300, 0), (200, 100), (100, 200) и (0, 300). Для наглядности проведём через все клетки, соответствующие инвестициям одинаковых сумм параллельные линии (как это показано в табл. 2). В частности, на линии, соответствующей инвестиции 300 тыс. руб., расположены возможные значения прибыли 90, 120, 100, 110. Выбираем из значений данных клеток максимальное и обводим его в кружок – это значение 120 тыс. руб., оно находится в клетке (200, 100). В нашем случае это означает следующее: если ко второму этапу мы подошли с капиталом 300 тыс. рублей, то наиболее выгодно будет вложить 200 тысяч во второе предприятие и 100 тысяч в третье, что принесёт прибыль в 120 тыс. рублей. Аналогично поступаем с группами других клеток, сумма номеров которых одинакова (то есть соединёнными линиями) – на каждой линии выбираем максимальное значение и обводим его в кружок. Результаты заносим в первые две строки табл. 3. В первой строке указываем суммарный инвестируемый капитал, под ним указывается способ его распределения между вторым и третьим предприятием (в виде суммы двух чисел, первое из которых соответствует вложению во второе предприятие, а второе – вложению в третье, то есть номера выбранных клеток). Во второй строке указываем соответствующую прибыль (число, обведенное в кружок в табл. 2). Обратим внимание на то, что существуют различные варианты размещения капиталов, приносящие равные результаты. Например, при размещении 500 тыс. рублей (линия, начинающаяся от клетки и заканчивающаяся клеткой (500, 0) в табл. 2), наибольшее значение прибыли (190 тыс. руб.) достигается сразу в трёх клетках (500,0), (400, 100) и (200, 300). В таком случае мы можем выбрать любую из этих трёх клеток (либо лицо, принимающее решение, определяет наилучший вариант, руководствуясь какими-то дополнительными факторами, не указанными в задаче). Для определённости выберем клетку (200, 300).

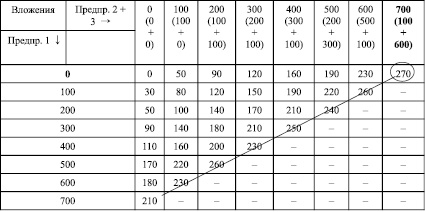
Прибыль от вложения средств в первое, второе и третье предприятия

Итак, вторая строка табл. 3 соответствует наилучшим результатам инвестирования средств, указанных в первой строке, при условии, что в первое предприятие вложений не делалось. Продолжим заполнение табл. 3. Теперь в первый столбец внесём возможные инвестиции в первое предприятие, а во второй столбец – соответствующие прибыли (копируется столбец табл. 1, соответствующий прибыли от первого предприятия). В остальные клетки заносятся соответствующие прибыли от суммарных инвестиций. Например, клетка (100, 100) теперь соответствует инвестированию 100 тысяч рублей в первое предприятие (что принесёт прибыль 30 тыс. рублей) и наилучшему суммарному инвестированию ста тысяч рублей во второе и третье предприятие (полученному из табл. 2 и равному 50 тыс. рублей). Поэтому в клетку (100, 100) заносится значение 80 = 30 + 50. Самым большим числом в табл. 3 является число 270, находящееся в клетке (0, 700). Это значение соответствует максимальной прибыли, которая может быть получена в данной экономической ситуации. Такой финансовый результат достигается, если вкладывать 0 тыс. рублей в первое предприятие и 700 тысяч рублей во второе и третье, что видно из номера клетки (0, 700). Оптимальное распределение 700 тысяч рублей между вторым и третьим предприятиями уже было найдено ранее (оно указано в верхней строке таблицы под числом 700) – это вложение 100 тысяч во второе предприятие и 600 тысяч в третье предприятие (клетка (100, 600) из табл. 2). Таким образом, мы определили максимальную прибыль 270 тысяч рублей от инвестирования 700 тысяч в три рассматриваемых предприятия. Оптимальный план действий – инвестировать 100 тысяч во второе предприятие (прибыль в 50 тысяч рублей) и 600 тысяч в третье предприятие (прибыль 220 тысяч рублей).

Заметим также, что из последней таблицы мы можем сразу получить оптимальные планы инвестирования меньших сумм (600 тысяч, 500 тысяч и т.д.). Эти результаты могут быть использованы при решении других, более сложных, задач (например, если можно инвестировать средства в 4 и более предприятий). В нашем случае, когда имеется только три предприятия, для решения задачи в последней таблице достаточно заполнить только нижнюю диагональ, через которую в табл. 3 проведена линия – решение ещё более сокращается.

При решении этой задачи обучаемым нет необходимости выписывать все приводимые здесь пояснения – всё решение целиком сводится к заполнению двух таблиц – табл. 2 и табл. 3 и занимает, таким образом, менее одной страницы. Для сравнения, решение той же задачи традиционным способом, представленным в работе [2], занимает 6 страниц и требует выписывания реккурентного соотношения, 15 матриц столбцов и двух итоговых таблиц, и это без учёта описания общего метода решения. Не меньший объем занимает и решение аналогичных задач, приводимых в других работах [1, 3, 5]. Тем же методом можно решать и большинство других прикладных экономических задач, относящихся к теме «динамическое программирование» – задачу об оптимальном назначении, об оптимальной загрузке судна, задачу о найме сезонных рабочих, об оптимальном использовании оборудования и другие. Разумеется, описываемый метод решения не требует выписывания рекуррентного соотношения, поэтому этот метод не годится для тех студентов, в программах обучения которых тема «рекуррентные соотношения» имеет самостоятельное значение, например, для студентов-математиков прикладных направлений, изучающих исследование операций. Однако, по нашему мнению, данный метод вполне пригоден для студентов менеджеров и экономистов, в особенности бакалавров, задачей обучения которых является подготовка не к теоретическим математическим исследованиям, а к практическому применению разработанного математического аппарата в реальных ситуациях. Поскольку большинство наиболее распространённых практических задач удается решить данным методом, ему следует отдать предпочтение также в связи с его большей доступностью для понимания, а также с меньшим временем, затрачиваемым на решение задач.

Рецензенты:

Лебедев А.М., д.т.н., профессор кафедры естественно-научных дисциплин, ФГБОУ ВПО «Ульяновское высшее авиационное училище гражданской авиации (институт)», г. Ульяновск;

Ильмушкин Г.М., д.п.н., профессор, заведующий кафедрой высшей математики, Димитровградский инженерно-технологический институт (филиал ФГАОУ ВПО «Национальный исследовательский ядерный университет «МИФИ»), г. Димитровград.

Источник