Метод чистой текущей приведенной стоимости инвестиции

Чистая текущая стоимость NPV

Чистая текущая стоимость — сумма текущих стоимостей всех спрогнозированных, с учетом ставки дисконтирования, денежных потоков.

Метод чистой текущей стоимости (NPV) состоит в следующем.
1. Определяется текущая стоимость затрат (Io), т.е. решается вопрос, сколько инвестиций нужно зарезервировать для проекта.
2. Рассчитывается текущая стоимость буду?их денежных поступлений от проекта, для чего доходы за каждый год CF (кеш-флоу) приводятся к текущей дате.

Результаты расчетов показывают, сколько средств нужно было бы вложить сейчас для получения запланированных доходов, если бы ставка доходов была равна барьерной ставке (для инвестора ставке процента в банке, в ПИФе и т.д., для предприятия цене совокупного капитала или через риски). Подытожив текущую стоимость доходов за все годы, получим общую текущую стоимость доходов от проекта (PV):

3. Текущая стоимость инвестиционных затрат (Io) сравнивается с текущей стоимостью доходов (PV). Разность между ними составляет чистую текущую стоимость доходов (NPV):

NPV показывает чистые доходы или чистые убытки инвестора от помещения денег в проект по сравнению с хранением денег в банке. Если NPV > 0, то можно считать, что инвестиция приумножит богатство предприятия и инвестицию следует осуществлять. При NPV 0 относят к затратным инвестициям (пример: средства выделенные на экологическую программу).

Определяется: как сумма текущих стоимостей всех спрогнозированных, с учетом барьерной ставки (ставки дисконтирования), денежных потоков.

Характеризует: эффективность инвестиции в абсолютных значениях, в текущей стоимости.

Синонимы: чистый приведенный эффект, чистый дисконтированный доход, Net Present Value.

Акроним: NPV

Недостатки: не учитывает размер инвестиции, не учитывается уровень реинвестиций.

Критерий приемлемости: NPV >= 0 (чем больше, тем лучше)

Условия сравнения: для корректного сравнения двух инвестиций они должны иметь одинаковый размер инвестиционных затрат.

Пример №1. Расчет чистой текущей стоимости.
Размер инвестиции — 115000$.
Доходы от инвестиций в первом году: 32000$;
во втором году: 41000$;
в третьем году: 43750$;
в четвертом году: 38250$.
Размер барьерной ставки — 9,2%

Пересчитаем денежные потоки в вид текущих стоимостей:
PV₁ = 32000 / (1 + 0,092) = 29304,03$
PV₂ = 41000 / (1 + 0,092) 2 = 34382,59$
PV₃ = 43750 / (1 + 0,092) 3 = 33597,75$
PV₄ = 38250 / (1 + 0,092) 4 = 26899,29$

NPV = (29304,03 + 34382,59 + 33597,75 + 26899,29) — 115000 = 9183,66$

Ответ: чистая текущая стоимость равна 9183,66$.

Формула для расчета показателя NPV (чистой текущей стоимости) с учетом переменной барьерной ставки:

NPV — чистая текущая стоимость;
CFt — приток (или отток) денежных средств в период t;
It — сумма инвестиций (затраты) в t-ом периоде;
ri — барьерная ставка (ставка дисконтирования), доли единицы (при практических расчетах вместо (1+r) t применяют (1+r₀)*(1+r₁)*. *(1+r_t), т.к. барьерная ставка может сильно меняться из-за инфляции и других составляющих);

n — суммарное число периодов (интервалов, шагов) t = 1, 2, . n (обычно нулевой период подразумевает затраты произведенные для реализации инвестиции и количество периодов не увеличивается).

Пример №2. NPV при переменной барьерной ставке.
Размер инвестиции — $12800.
Доходы от инвестиций в первом году: $7360;
во втором году: $5185;
в третьем году: $6270.
Размер барьерной ставки — 11,4% в первом году;
10,7% во втором году;
9,5% в третьем году.
Определите значение чистой текущей стоимости для инвестиционного проекта.

n =3.
Пересчитаем денежные потоки в вид текущих стоимостей:
PV₁ = 7360 / (1 + 0,114) = $6066,82
PV₂ = 5185 / (1 + 0,114)/(1 + 0,107) = $4204,52
PV₃ = 6270 / (1 + 0,114)/(1 + 0,107)/(1 + 0,095) = $4643,23

NPV = (6066,82 + 4204,52 + 4643,23) — 12800 = $2654,57

Ответ: чистая текущая стоимость равна $2654,57.

Правило, согласно которому, из двух проектов, с одинаковыми затратами, выбирается проект с большим NPV действует не всегда. Проект с меньшим NPV, но с коротким сроком окупаемости может быть выгоднее проекта с большим NPV.

Пример №3. Сравнение двух проектов.
Стоимость инвестиции для обоих проектов равна 100 рублям.
Первый проект генерирует прибыль равную 130 рублям по окончании 1 года, а второй 140 рублей через 5 лет.
Для простоты расчетов считаем барьерные ставки равными нулю.
NPV₁ = 130 — 100 = 30 руб.
NPV₂ = 140 — 100 = 40 руб.

Но при этом годовая доходность, рассчитанная по модели IRR, будет у первого проекта равна 30%, а у второго 6,970%. Ясно, что будет принят первый инвестиционный проект, несмотря на меньший NPV.

Для более точного определения чистой текущей стоимости денежных потоков применяют показатель «модифицированная чистая текущая стоимость (MNPV)».

Пример №4. Анализ чувствительности.
Размер инвестиции — 12800$.
Доходы от инвестиций в первом году: $7360;
во втором году: $5185;
в третьем году: $6270.
Размер барьерной ставки — 11,4% в первом году;
10,7% во втором году;
9,5% в третьем году.
Рассчитайте, как повлияет на значение чистой текущей стоимости увеличение доходов от инвестиции на 30%?

Исходное значение чистой текущей стоимости было рассчитано в примере №2 и равна NPV_исх = 2654,57.

Пересчитаем денежные потоки в вид текущих стоимостей с учетом данных анализа чувствительности:
PV_{1 ач} = (1 + 0,3) * 7360 / (1 + 0,114) = 1,3 * 6066,82 = $7886,866
PV_{2 ач} = (1 + 0,3) * 5185 / (1 + 0,114)/(1 + 0,107) = 1,3 * 4204,52 = $5465,876
PV_{3 ач} = (1 + 0,3) * 6270 / (1 + 0,114)/(1 + 0,107)/(1 + 0,095) = 1,3 * 4643,23 = $6036,199

Определим изменение чистой текущей стоимости: (NPV_ач — NPV_исх) / NPV_исх * 100% =
= (6036,199 — 2654,57) / 2654,57 * 100% = 127,39%.
Ответ. Увеличение доходов от инвестиции на 30% привело к увеличению чистой текущей стоимости на 127,39%.

Примечание. Дисконтирование денежных потоков при меняющейся во времени барьерной ставке (норме дисконта) соответствует «Методическим указаниям № ВК 477 . » п.6.11 (стр. 140).

Главная Методики финансового и инвестиционного анализа Инвестиционный анализ Чистая текущая стоимость

Copyright © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.

Источник

Discovered

О финансах и не только…

Чистая текущая стоимость (NPV)

В данной статье мы рассмотрим, что такое чистая текущая стоимость (NPV), какой экономический смысл она имеет, как и по какой формуле рассчитать чистую текущую стоимость, рассмотрим некоторые примеры расчёта, в том числе при помощи формул MS Exel.

Что такое чистая текущая стоимость (NPV)?

При вложении денег в любой инвестиционный проект ключевым моментом для инвестора является оценка экономической целесообразности такого инвестирования. Ведь инвестор стремится не только окупить свои вложения, но и ещё что-то заработать сверх суммы первоначальной инвестиции. Кроме того, задачей инвестора является поиск альтернативных вариантов инвестирования, которые бы при сопоставимых уровнях риска и прочих условиях инвестирования принесли бы более высокую прибыль. Одним из методов подобного анализа является расчёт чистой текущей стоимости инвестиционного проекта.

Чистая текущая стоимость (NPV, Net Present Value) – это показатель экономической эффективности инвестиционного проекта, который рассчитывается путём дисконтирования (приведения к текущей стоимости, т.е. на момент инвестирования) ожидаемых денежных потоков (как доходов, так и расходов).

Чистая текущая стоимость отражает прибыль инвестора (добавочную стоимость инвестиций), которую инвестор ожидает получить от реализации проекта, после того, как денежные притоки окупят его первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с осуществлением такого проекта.

В отечественной практике термин «чистая текущая стоимость» имеет ряд тождественных обозначений: чистая приведённая стоимость (ЧПС), чистый приведённый эффект (ЧПЭ), чистый дисконтированный доход (ЧДД), Net Present Value (NPV).

Формула расчёта NPV

Для расчёта NPV необходимо:

1. Составить прогнозный график денежных потоков по инвестиционному проекту в разрезе периодов. Денежные потоки должны включать как доходы (притоки средств), так и расходы (осуществляемые инвестиции и прочие затраты по реализации проекта).
2. Определить размер ставки дисконтирования. По сути, ставка дисконтирования отражает предельную норму стоимости капитала инвестора. Например, если для инвестирования будут использованы заёмные средства банка, то ставкой дисконтирования будет являться эффективная ставка процента по кредиту. Если же будут использованы собственные средства инвестора, то за ставку дисконтирования может быть взята ставка процента по банковскому депозиту, ставка доходности по государственным облигациям и т.п.

Расчёт NPV осуществляется по следующей формуле:

где
NPV (Net Present Value) — чистая текущая стоимость инвестиционного проекта;
CF (Cash Flow) — денежный поток;
r — ставка дисконтирования;
n — общее количество периодов (интервалов, шагов) i = 0, 1, 2, …, n за весь срок инвестирования.

В данной формуле CF₀ соответствует объёму первоначальных инвестиций IC (Invested Capital), т.е. CF₀ = IC. При этом денежный поток CF₀ имеет отрицательное значение.

Поэтому, вышеуказанную формулу можно модифицировать:

Если инвестиции в проект осуществляются не одномоментно, а на протяжении ряда периодов, то инвестиционные вложения также должны быть продисконтированны. В таком случае формула NPV проекта примет следующий вид:

Практическое применение NPV (чистой текущей стоимости)

Расчёт NPV позволяет оценить целесообразность инвестирования денежных средств. Возможны три варианта значения NPV:

1. NPV > 0. Если чистая текущая стоимость имеет положительное значение, то это свидетельствует о полной окупаемости инвестиций, а значение NPV показывает итоговый размер прибыли инвестора. Инвестиции являются целесообразными в следствие их экономической эффективности.
2. NPV = 0. Если чистая текущая стоимость имеет нулевое значение, то это свидетельствует об окупаемости инвестиций, но инвестор при этом не получает прибыль. Например, если были использованы заёмные средства, то денежные потоки от инвестиционных вложений позволят в полном объеме рассчитаться с кредитором, в том числе выплатить причитающиеся ему проценты, но финансовое положение инвестора при этом не изменится. Поэтому следует поискать альтернативные варианты вложения денежных средств, которые бы имели положительный экономический эффект.
3. NPV

В результате проведённых расчётов проект А следует отклонить, проект Б находится в точке безразличия для инвестора, а вот проекты В и Г следует использовать для вложения средств. При этом, если необходимо выбрать только один проект, то предпочтение следует отдать проекту В, невзирая на то, что сумму недисконтированных денежных потоков за 10 лет он генерирует меньше, чем проект Г.

Преимущества и недостатки NPV

К положительным моментам методики NPV можно отнести:

• чёткие и простые правила для принятия решений относительно инвестиционной привлекательности проекта;
• применение ставки дисконтирования для корректировки суммы денежных потоков во времени;
• возможность учета премии за риск в составе ставки дисконтирования (для более рискованных проектов можно применить повышенную ставку дисконтирования).

К недостаткам NPV можно отнести следующие:

• трудность оценки для сложных инвестиционных проектов, которые включают в себя множество рисков особенно в долгосрочной перспективе (требуется корректировка ставки дисконтирования);
• сложность прогнозирования будущих денежных потоков, от точности которых зависит расчетная величина NPV;
• формула NPV не учитывает реинвестирование денежных потоков (доходов);
• NPV отражает только абсолютную величину прибыли. Для более корректного анализа необходимо также дополнительно производить расчёт и относительных показателей, например таких как рентабельность инвестиций, внутренняя норма доходности (IRR).

Источник

NPV (чистая приведенная стоимость)

NPV (аббревиатура, на английском языке — Net Present Value), по-русски этот показатель имеет несколько вариаций названия, среди них:

• чистая приведенная стоимость (сокращенно ЧПС) — наиболее часто встречающееся название и аббревиатура, даже формула в Excel именно так и называется;
• чистый дисконтированный доход (сокращенно ЧДС) — название связано с тем, что денежный потоки дисконтируются и только потом суммируются;
• чистая текущая стоимость (сокращенно ЧТС) — название связано с тем, что все доходы и убытки от деятельности за счет дисконтирования как бы приводятся к текущей стоимости денег (ведь с точки зрения экономики, если мы заработаем 1 000 руб. и получим потом на самом деле меньше, чем если бы мы получили ту же сумму, но сейчас).

NPV — это показатель прибыли, которую получат участники инвестиционного проекта. Математически этот показатель находится путем дисконтирования значений чистого денежного потока (вне зависимости от того отрицательный он или положительный).

Чистый дисконтированный доход может быть найден за любой период времени проекта начиная с его начала (за 5 лет, за 7 лет, за 10 лет и так далее) в зависимости от потребности расчета.

Для чего нужен

NPV — один из показателей эффективности проекта, наряду с IRR, простым и дисконтированным сроком окупаемости. Он нужен, чтобы:

1. понимать какой доход принесет проект, окупится ли он в принципе или он убыточен, когда он сможет окупиться и сколько денег принесет в конкретный момент времени;
2. для сравнения инвестиционных проектов (если имеется ряд проектов, но денег на всех не хватает, то берутся проекты с наибольшей возможностью заработать, т.е. наибольшим NPV).

Формула расчета

Для расчета показателя используется следующая формула:

, где

• CF — сумма чистого денежного потока в период времени (месяц, квартал, год и т.д.);
• t — период времени, за который берется чистый денежный поток;
• N — количество периодов, за который рассчитывается инвестиционный проект;
• i — ставка дисконтирования, принятая в расчет в этом проекте.

Пример расчета

Для рассмотрения примера расчета показателя NPV возьмем упрощенный проект по строительству небольшого офисного здания. Согласно проекту инвестиций планируются следующие денежные потоки (тыс. руб.):

Статья	1 год	2 год	3 год	4 год	5 год
Инвестиции в проект	100 000
Операционные доходы	35 000	37 000	38 000	40 000
Операционные расходы	4 000	4 500	5 000	5 500
Чистый денежный поток	— 100 000	31 000	32 500	33 000	34 500

Коэффициент дисконтирования проекта — 10%.

Подставляя в формулу значения чистого денежного потока за каждый период (там где получается отрицательный денежный поток ставим со знаком минус) и корректируя их с учетом ставки дисконтирования получим следующий результат:

NPV = — 100 000 / 1.1 + 31 000 / 1.1 2 + 32 500 / 1.1 3 + 33 000 / 1.1 4 + 34 500 / 1.1 5 = 3 089.70

Расчет NPV в Excel

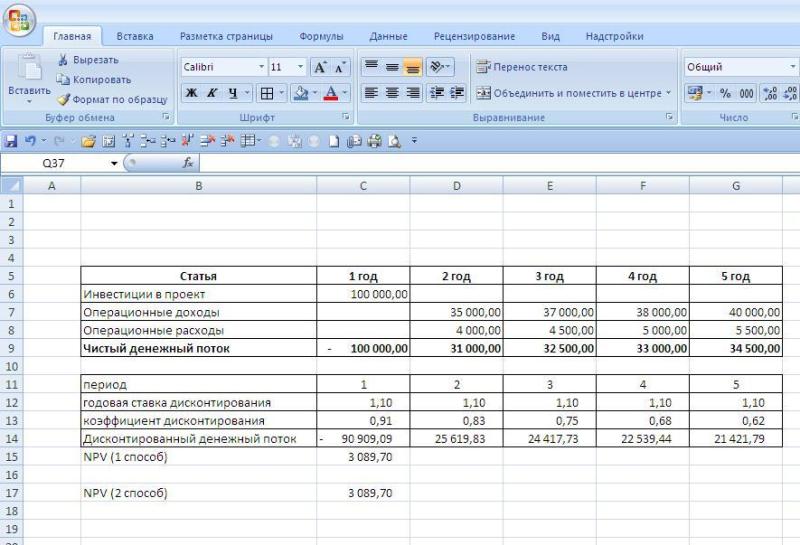
Чтобы проиллюстрировать как рассчитывается NPV в Excel, рассмотрим предыдущий пример заведя его в таблицы. Расчет можно произвести двумя способами

1. В Excel имеется формула ЧПС, которая рассчитывает чистую приведенную стоимость, для этого вам необходимо указать ставку дисконтирования (без знака проценты) и выделить диапазон чистого денежного потока. Вид формулы такой: = ЧПС (процент; диапазон чистого денежного потока).
2. Можно самим составить дополнительную таблицу, где продисконтировать денежный поток и просуммировать его.

Ниже на рисунке мы привели оба расчета (первый показывает формулы, второй результаты вычислений):

Как вы видите, оба метода вычисления приводят к одному и тому же результату, что говорит о том, что в зависимости от того, чем вам удобнее пользоваться вы можете использовать любой из представленных вариантов расчета.

Примеры расчета NPV в бизнес-планах

Увидеть как рассчитан показатель на конкретном примере бизнес-плана вы можете выбрав соответствующий документ в форме поиска или перейдя по ссылке ниже:

Источник

Читайте также:  Лучший драйвер nvidia майнинг