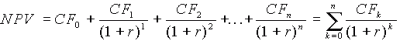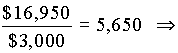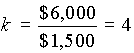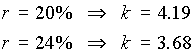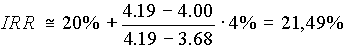7. 3. Метод чистого современного значения (npv — метод)
Этот метод основан на использовании понятия чистого современного значения (Net Present Value)

где CFi — чистый денежный поток, r — стоимость капитала, привлеченного для инвестиционного проекта.
Термин “чистое” имеет следующий смысл: каждая сумма денег определяется как алгебраическая сумма входных (положительных) и выходных (отрицательных) потоков. Например, если во второй год реализации инвестиционного проекта объем капитальных вложений составляет $15,000, а денежный доход в тот же год — $12,000, то чистая сумма денежных средств во второй год составляет ($3,000).
В соответствии с сущностью метода современное значение всех входных денежных потоков сравнивается с современным значением выходных потоков, обусловленных капитальными вложениями для реализации проекта. Разница между первым и вторым есть чистое современное значение, величина которого определяет правило принятия решения.
Шаг 1. Определяется современное значение каждого денежного потока, входного и выходного.
Шаг 2. Суммируются все дисконтированные значения элементов денежных потоков и определяется критерий NPV.
Шаг 3. Производится принятие решения:
для отдельного проекта: если NPV больше или равно нулю, то проект принимается;
для нескольких альтернативных проектов: принимается тот проект, который имеет большее значение NPV, если только оно положительное.
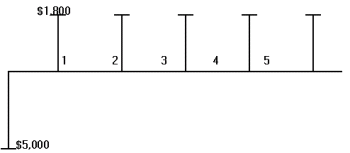
Пример 2. Руководство предприятия собирается внедрить новую машину, которая выполняет операции, производимые в настоящее время вручную. Машина стоит вместе с установкой $5,000 со сроком эксплуатации 5 лет и нулевой ликвидационной стоимостью. По оценкам финансового отдела предприятия внедрение машины за счет экономии ручного труда позволит обеспечить дополнительный входной поток денег $1,800. На четвертом году эксплуатации машина потребует ремонт стоимостью $300.
Экономически целесообразно ли внедрять новую машину, если стоимость капитала предприятия составляет 20%.
Решение. Представим условия задачи в виде лаконичных исходных данных.
Стоимость ремонта в 4-м году
Входной денежный поток за счет приобретения машины
Расчет произведем с помощью следующей таблицы.
Таблица 7.3. Расчет значения NPV
Наименование денежного потока
Входной денежный поток
Современное чистое значение (NPV)
* Множитель дисконтирования определяется с помощью финансовых таблиц.
В результате расчетов NPV = $239 > 0, и поэтому с финансовой точки зрения проект следует принять.
Сейчас уместно остановиться на интерпретации значения NPV. Очевидно, что сумма $239 представляет собой некоторый “запас прочности”, призванный компенсировать возможную ошибку при прогнозировании денежных потоков. Американские финансовые менеджеры говорят — это деньги, отложенные на “черный день”.
Рассмотрим теперь вопрос зависимости показателя и, следовательно, сделанного на его основе вывода от нормы доходности инвестиций. Другими словами, в рамках данного примера ответим на вопрос, что если показатель доходности инвестиций (стоимость капитала предприятия) станет больше. Как должно измениться значение NPV?
Расчет показывает, что при r = 24% получим NPV = ($186), то есть критерий является отрицательным и проект следует отклонить. Интерпретация этого феномена может быть проведена следующим образом. О чем говорит отрицательное значение NPV? О том, что исходная инвестиция не окупается, т.е. положительные денежные потоки, которые генерируются этой инвестицией не достаточны для компенсации, с учетом стоимости денег во времени, исходной суммы капитальных вложений. Вспомним, что стоимость собственного капитала компании — это доходность альтернативных вложений своего капитала, которое может сделать компания. При r = 20% компании более выгодно вложить деньги в собственное оборудование, которое за счет экономии генерирует денежный поток $1,800 в течение ближайших пяти лет; причем каждая из этих сумм в свою очередь инвестируется по 20% годовых. При r = 24% компании более выгодно сразу же инвестировать имеющиеся у нее $5,000 под 24% годовых, нежели инвестировать в оборудование, которое за счет экономии будет “приносить” денежный доход $1,800, который в свою очередь будет инвестироваться под 24% годовых.
Общий вывод таков: при увеличении нормы доходности инвестиций (стоимости капитала инвестиционного проекта) значение критерия NPV уменьшается.
Для полноты представления информации, необходимой для расчета NPV, приведем типичные денежные потоки.
Типичные входные денежные потоки:
дополнительный объем продаж и увеличение цены товара;
уменьшение валовых издержек (снижение себестоимости товаров);
остаточное значение стоимости оборудования в конце последнего года инвестиционного проекта (так как оборудование может быть продано или использовано для другого проекта);
высвобождение оборотных средств в конце последнего года инвестиционного проекта (закрытие счетов дебиторов, продажа остатков товарно-материальных запасов, продажа акций и облигаций других предприятий).
Типичные выходные потоки:
начальные инвестиции в первый год(ы) инвестиционного проекта;
увеличение потребностей в оборотных средствах в первый год(ы) инвестиционного проекта (увеличение счетов дебиторов для привлечения новых клиентов, приобретение сырья и комплектующих для начала производства);
ремонт и техническое обслуживание оборудования;
дополнительные непроизводственные издержки (социальные, экологические и т. п.).
Ранее было отмечено, что результирующие чистые денежные потоки, призваны обеспечить возврат инвестированной суммы денег и доход для инвесторов. Рассмотрим, как происходит разделение каждой денежной суммы на эти две части с помощью следующего иллюстрирующего примера.
Пример 3. Предприятие планирует вложить деньги в приобретение нового приспособления которое стоит $3,170 и имеет срок службы 4 года с нулевой остаточной стоимостью. Внедрение приспособления по оценкам позволяет обеспечить входной денежный поток $1,000 в течение каждого года. Руководство предприятия позволяет производить инвестиции только в том случае, когда это приводит к отдаче хотя бы 10% в год.
Решение. Сначала произведем обычный расчет чистого современного значения.
Источник
Оценки комплексных показателей эффективности инвестиций
| Раздел: Управление финансами | |
| Автор(ы): В.П.Савчук, директор ДЦППП | размещено: 25.04.2001 обращений: 66642 |
 |
 |
 |  |
|  | |
 | ||||
 | |||||||||||||||||||||
 | |||||||||||||||||||||
 | |||||||||||||
 | Окончательное решение об эффективности инвестиций принимается на основе следующих комплексных показателей:
Метод дисконтированного периода окупаемости (DPB-метод)Суть метода заключается в дисконтировании всех денежных потоков, генерируемых заданной инвестицией и их суммирования последовательно до тех пор пока не будет покрыта исходная инвестиция. Рассмотрим этот метод на конкретном примере. Пусть объем капитальных вложений проекта составляет $1,000,000 и рассчитан на четыре года. Проект генерирует следующие денежные потоки : по годам 500, 400, 300, 100 (тысячах USD). Расчет дисконтированного срока осуществляется по следующей схеме. Показатель дисконтирования — 10%. Таблица 1. Схема расчета дисконтированного срока Чистый денежный поток (ЧДП) | ||||||||||||
| Стоимость машины | $5,000 |
| Время проекта | 5 лет |
| Остаточная стоимость | $0 |
| Стоимость ремонта в 4-м году | $300 |
| Входной денежный поток за счет приобретения машины | $1,800 |
| Показатель дисконта | 20% |
Наименование денежного потока
Денежный поток
Дисконтирование множителя 20%
Настоящее значение денег
Исходная инвестиция
Входной денежный поток
Ремонт машины
($145)
В результате расчетов NPV=$239>0, потому с экономической точки зрения проект следует принять.
Интерпретация значения NPV: сумма $239 — «запас прочности», призванный компенсировать возможную ошибку при прогнозировании денежных потоков. Американские финансовые менеджеры говорят — это деньги, отложенные на «черный день».
Метод внутренней нормы прибыльности (IRR-метод)
По определению внутренняя норма прибыльности (IRR) — это значение показателя дисконта, при котором настоящее значение инвестиции равно настоящему значению потоков денежных средств за счет инвестиций, или значение показателя дисконта, при котором обеспечивается нулевое значение чистого настоящего значения инвестиционного проекта, расчет IRR проводится по формуле:
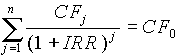
CFj — входной денежный поток в j-ый период,
CF0 — настоящее значение инвестиции.
Решая уравнение, находим IRR. Решение может быть только приближенным.
Пример. На покупку машины требуется $16,950. Машина в течение 10 лет будет экономить ежегодно $3,000. Остаточная стоимость машины равна нулю. Надо найти IRR.
Найдем отношение требуемого значения инвестиции к ежегодному притоку денег, которое будет совпадать с множителем какого-либо показателя дисконтирования (коэффициента пересчета)
Множитель, который определяется показателем дисконтирования. По таблице находим, что для n=10 множитель, который соответствует r=12%.
Денежный поток
12% коэффиц. пересчета
Настоящее значение
$16,950
Таким образом IRR=12%. Но здесь мы оказались удачливыми. В общем случае надо пользоваться более сложными методами.
Требуемая инвестиция — $6,000
Годовая экономия — 1,500
Полезная жизнь — 10 лет
Коэффициент пересчета:
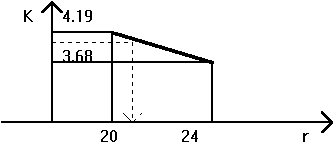
Значит IRR находится между этими значениями и может быть определено с помощью интерполяции.
Существуют более точные методы определения IRR, которые предполагают использование специального финансового калькулятора или системы EXCEL.
Источник