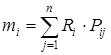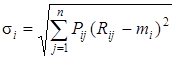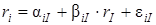Математическое ожидание доходности формула

Курс лекций «Основы финансового менеджмента»

5.5. Количественное измерение риска

Средняя арифметическая ожидаемых доходностей ( r i ) инвестиций, взвешенная по вероятности возникновения отдельных значений, называется математическим ожиданием. Условимся называть эту величину средней ожидаемой доходностью :

, (5.5.1)

где p i – вероятность получения доходности r i .

В статистике количественным измерителем степени разброса значений переменной вокруг ее средней величины (математического ожидания) является показатель дисперсии ( σ 2 ):

(5.5.2)

Квадратный корень из дисперсии называется средним квадратическим или стандартным отклонением σ :

(5.5.3)

Данный показатель используется в финансовом менеджменте для количественного измерения степени риска планируемых инвестиций. Чем больше разброс ожидаемых значений доходности вложений вокруг их среднеарифметической величины, тем выше риск, сопряженный с данным вложением . Фактическая величина доходности может быть как значительно выше, так и значительно ниже ее средней величины.

Практическая ценность такого подхода заключается не только (и не столько) в применении статистических формул, а в осознании необходимости многовариантного планирования инвестиционных решений. Любые ожидаемые результаты этих решений могут носить лишь вероятностный характер. От финансиста требуется не только правильно применить формулу расчета доходности инвестиций, но и дать количественную оценку вероятности возникновения конкретного результата. Как минимум, необходимо планировать не менее трех вариантов развития событий : оптимистический, пессимистический и наиболее вероятный. Полная вероятность возникновения всех этих вариантов должна быть равна 1.

Например, оценивая две акции А и Б, инвестор пришел к выводу, что распределение вероятностей их ожидаемой доходности можно представить следующим образом:

Источник

Математическое ожидание прибыли

Математическое ожидание (МО) – это сумма произведения вероятностей получения прибыли со сделки, умноженная на фактический результат каждого трейда:

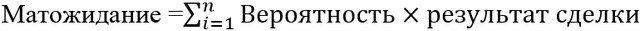
, где n – количество трейдов.

Убыточные сделки, подставляются в формулу с отрицательным знаком и при суммировании вычитаются, поэтому матожидание принимает как положительные, так и отрицательные значения.

Вероятности положительного исхода (или риска) на каждую сделку заменяют ее фактическим значением, добавляя соотношение среднего арифметического прибыли и убытка. В этом случае формула выглядит следующим образом:

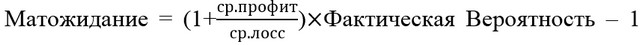
, где фактическая вероятность равна реальному проценту прибыльных сделок от общего числа совершенных трейдов.

Средний профит считается как сумма прибыльных сделок, деленная на их количество. Также рассчитывают средний убыток (ср. лосс), суммируя отрицательные значения и усредняя результаты трейдов.

Торговые платформы Форекс рассчитывают МО в режиме торгового отчета и в терминале тестера стратегий, используя упрощенные или видоизмененные формулы

Содержание

Расчет математического ожидания выигрыша в торговой платформе Metatrader

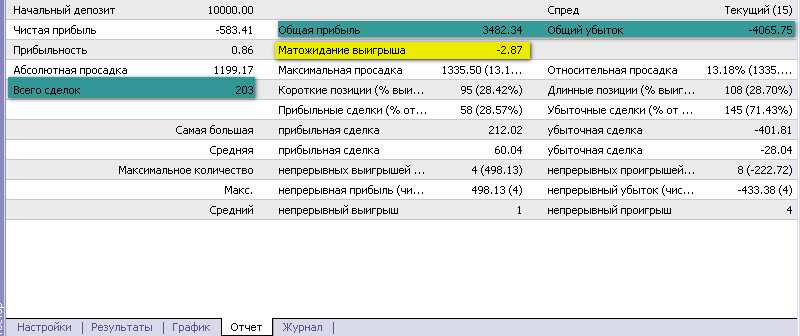
В распространенной платформе Metatrader математическое ожидание считается по формуле:

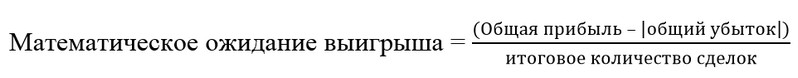
Такой упрощенный подход оправдан отсутствием надежных алгоритмов определения вероятности прибыли каждой сделки, зависимостью усредненных результатов профитов и убытков от волатильности.

Многолетние эмпирические исследования разработчиков Metatrader доказали эффективность оценки матожидания стратегий с использованием опубликованной выше формулы.

Практическое применение математического ожидания выигрыша на валютном рынке Форекс

Параметр матожидание оценивает потенциал собранной или приобретенной торговой системы до начала ее применения на реальном торговом счете, в режиме тестирования.

Тестер рассчитывает самостоятельно матожидание для автоматизированных систем (например, Советники в Metatrader) или отдельных индикаторов. В случаях ручного тестирования торговых систем, работающих по сигналам графических паттернов или условий, выходящих за рамки булевой логики, МО рассчитывается трейдером самостоятельно.

Как правило, отрицательное матожидание, указывает на вероятность полной потери депозита при длительном использовании стратегии. Значения положительного матожидания выше единицы, считаются надежным показателем потенциала протестированной системы.

Матожидание является экспресс-тестом профпригодности приобретаемого торгового робота. Чтобы оценить целесообразность покупки, робота запускают на различных исторических участках котировок, сравнивая полученное значение с заявленными данными Продавца.

После тестирования МО принимают за эталон, контролируя расхождение между тестовыми и реальными значениями торгуемой системы, чтобы не пропустить момент, когда она перестает приносить прибыль. Расхождения выше 10% трактуются как сигнал к оптимизации составных частей – индикаторов, логических правил поиска оптимальной точки покупки/продажи актива.

Споры о положительном и отрицательном значении математического ожидания

В среде трейдеров существует точка зрения, что отрицательное МО допустимо, если в целом стратегия приносит прибыль.

Общий положительный профит обеспечивают сделки с высокой нормой прибыли, тогда как основная часть убыточна, по причине малого уровня стоп лосса — отложенного ордера, ограничивающего потери.

Величина профита связана с волатильностью в активе и напрямую зависит от востребованности этого инструмента среди участников торгов. Непредсказуемое падение объемов и интереса моментально лишает стратегию «больших тейков», тогда как количество убыточных сделок из-за малого размера стоп лосса останется прежним..

Возможна зеркальная ситуация – стратегия на малых уровнях тейк профита приносит высокую прибыль, эксплуатируя флэтовые участки внутри сессии. Стопы в этом случае вынужденно многократно превышают прибыль – «прорывы» и «ложные проколы» границ флета имеют природу импульсов с высоким диапазоном.

Соотношение флета и тренда меняется непредсказуемо, поэтому нельзя точно рассчитать вероятность, когда выросшие до максимума направленные движения принесут размер убытка, который невозможно «отработать» малыми тейками.

Правило сбора статистических данных для расчета математического ожидания профита

Расчеты математического ожидания считаются достоверными если:

данные включают исторический период от 2000 до 10 000 свечей или баров «рабочего таймфрейма»; тесты в равной степени содержат участки растущего, падающего тренда и флэта; волатильность не имеет сильных отклонений от исторических значений (нет кризисных явлений или панических распродаж).

Тактические приемы по повышению значения математического ожидания

Математическое ожидание сильно зависит от выбора тактики фиксации прибыли и ограничения потерь. Прежде чем принять решение расстаться с найденной или разработанной стратегией, по причине невысокого результата у МО, следует обратить внимание на соотношение стопов и тейков.

Малый размер ограничения убытков приводит к увеличению количества отрицательных сделок и накоплению убытков. Если трейдер торгует парой EUR/USD внутри дня, он должен учитывать, что «торговый шум» в среднем составляет 30 пунктов и приведет к частому срабатыванию stop loss, расположенных в этой зоне.

Соотношение тейк/стоп как 2 к 1 увеличивает значение матожидания. Считается, что тейки и стопы не должны быть ниже паритета (1 к 1).

Уменьшение количества сделок может привести к росту значения МО. Трейдеры используют временные фильтры, торгуя в течение сессии на участках, совпадающих по времени с работой фондовых бирж стран, к которым относятся валюты пары.

Повышение качества входов – покупок или продаж валютных пар. В торговую систему вводятся фильтры, разрешающие сделку в значимых точках. Таковыми являются – исторические максимумы и минимумы, свечи, совпадающие по тренду на младших и старших таймфреймах, показания индикаторов с большим (от 50) периодом и т.д.

Особенности математического ожидания при скальпинге

Скальпинг характеризуется большим количеством сделок внутри дня с низким положительным значением МО. Малый размер стопов в этом случае составляет исключение, оправданное высокой активностью торгов. При небольшом превалировании прибыли над убытком заработок приносит большое количество сделок внутри дня.

В остальных тактических правилах исключений нет – скальпер применяет фиксированное значение тейка, превосходящее по величине уровень стопа. Поиск оптимального значения матожидания достигается за счет подбора времени удерживания сделки, скальпер не должен «пересиживать» или работать, когда нет волатильности.

Рассматриваемый параметр не определяет в одиночку целесообразность принятия стратегии. Оценка производительности основана на комплексном анализе результатов тестирования.

Источник

ManageFavor

Разработка стратегии и структуры компании

В настоящее время важнейшей проблемой руководства отечественных предприятий становится поиск путей в условиях усиления международной конкуренции .

Самоменеджмент — это относительно новое понятие в управленческой науке. Его возникновение во многом связано с переосмыслением содержания деятельности личности и более глубоким пониманием процессов самодеятельности, протекающих внутри организации.

Сущность, значение, типы портфеля ценных бумаг

Математическое ожидание дохода по i-й ценной бумаге (mi) можно рассчитать следующим образом:

Где:i — возможный доход по i-й ценной бумаге;ij — вероятность получения дохода;

n — количество ценных бумаг.

Для измерения степени риска служат показатели дисперсии, то есть, чем масштабнее по своей широте рассеивание величин возможных доходов, тем вероятнее опасность неполучения ожидаемого дохода. Мерой такого рассеивания выступает среднеквадратическое отклонение:

Каждому инвестиционному портфелю свойственны такие две основополагающие величины:

(3)

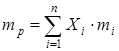
где:i — доля общего вложения, которая приходится на i-ю ценную бумагу;i — ожидаемая доходность i-й ценной бумаги, %;p — ожидаемая доходность портфеля, %;

· мера риска — среднеквадратическим отклонением доходности от ожидаемого значения

(4)

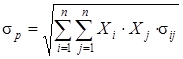
sp — мера риска портфеля;

sij — ковариация между доходностями i-й и j-й ценных бумаг;i и Xj — доли общего вложения, приходящиеся на i-ю и j-ю ценные бумаги;- число ценных бумаг портфеля [3, с. 1040].

В отличие от модели Марковица, модель Шарпа, которая разработана в 1960-х гг., требует гораздо меньший объем информации.

Анализируя поведение акций на рынке, Шарп пришел к следующему выводу: нет необходимости непременно определять корреляцию каждой из всего огромного множества акций друг с другом, а достаточным является выявление, того, каким образом каждая из акций находится во взаимодействии со всем рынком.

Поскольку такой анализ на уровне целого рынка сопряжен со значительными сложностями, то достаточным является выбор некоторого количества выбранных ценных бумаг, которые способны дать достаточно точную характеристику движению всего рынка. В роли именно такого показателя и используются фондовые индексы.

Шарп предложил b-фактор, который в нынешней теории портфеля играет особенно важную роль:

, (5)

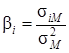
siM — ковариация темпов роста курса ценной бумаги и темпов роста рынка;

s2M — дисперсия доходности рынка.

Данный показатель призван раскрывать степень риска бумаги, иллюстрируя, во сколько раз изменение цены бумаги выше изменения рынка в целом. Таким образом, если b>1, то данная бумага принадлежит к числу финансовых инструментов с высоким риском, а если b<1, то цена бумаги изменялась медленнее, чем рынок в целом и данную бумагу можно отнести к числу относительно безрисковых активов. Если же вдруг b<0, то движение стоимости данной бумаги является противоположным движению рынка в целом [8].

Зависимость доходности ценной бумаги от индекса можно выразить такой формулой:

где ri — доходность ценной бумаги i за данный период;I — доходность на рыночный индекс I за этот же период;

aiI — коэффициент смещения;

b iI — коэффициент наклона;

e iI — случайная погрешность [6, с. 372]

Управление прибылью торгового предприятия
Предметом изучения в данной курсовой работе является прибыль. Прибыль является важнейшей категорией рыночной экономики и одним из важнейших показателей деятельности предприятия. При переходе .

Стратегия продвижения товаров на инструментальном уровне
Теоретические основы разработки стратегии продвижения товаров .

Источник

Доходность ценных бумаг. Основные методы оценки и прогнозирования

Ни для кого не секрет, что основной целью инвестиций в ценные бумаги является получение максимально возможной прибыли при сохранении приемлемого уровня риска. В этой статье я расскажу вам о том, какие виды ценных бумаг обладают потенциально большим потенциалом доходности. Вы узнаете о том из чего складывается их доходность и каким образом она вычисляется. Наконец, мы с вами подробно поговорим о том, как можно провести предварительную оценку и рассчитать ожидаемую доходность ценных бумаг ещё на этапе их выбора.

Какие бумаги потенциально самые прибыльные

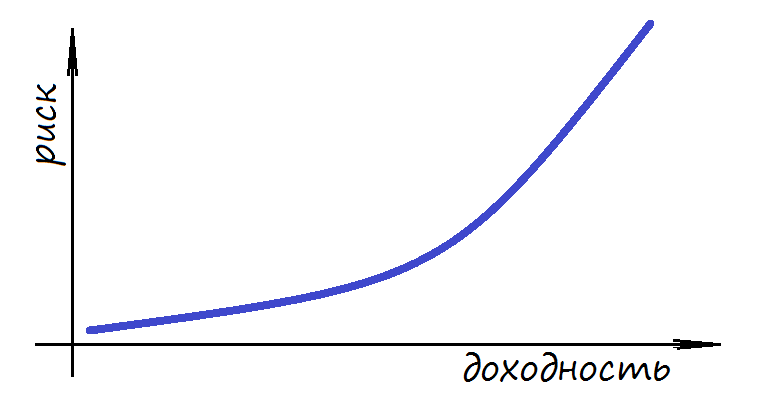
Ответ на этот вопрос довольно прост: самый большой потенциал в плане прибыли имеют ценные бумаги с таким же большим уровнем риска. Чем выше риск, который готов взять на себя инвестор, тем выше тот доход, который он может в итоге получить. Ключевое слово в данном случае – «может», поскольку с увеличением степени риска вероятность получения дохода постепенно тает.

Соотношение риска и доходности

То есть, другими словами, увеличивая степень риска инвестор одновременно и повышает свою потенциальную доходность, и снижает вероятность её получения. Поэтому в инвестициях так важно найти ту самую золотую середину, тот уровень риска при котором можно рассчитывать на относительно высокую прибыль с достаточно большой вероятностью её получения.

Минимальным риском, но и наименьшей степенью доходности отличаются такие бумаги, как государственные облигации. Обычно процент по ним сопоставим с доходностью банковских депозитов и едва превышает текущий уровень инфляции. Инвестирование в бумаги данного типа целесообразно в тех случаях, когда основной целью является не приумножение, а сохранение своих денежных средств.

На ступеньку выше стоят корпоративные облигации крупнейших компаний. Они также обладают достаточной степенью надёжности, но позволяют получить чуть большую прибыль (в отличие от бумаг выпущенных государством). Ещё выше по доходности – акции тех же самых компаний, но и риск по ним тоже чуть выше. Облигация по природе своей — долговая ценная бумага, то есть она подразумевает возврат долга и процентов по нему в любом случае. А вот акция — бумага долевая. Она даёт своему владельцу долю в бизнесе компании её выпустившей, но вместе с этим он принимает на себя и определённые риски (в частности, убытки в результате возможного снижения курса акций).

Ещё более рисковыми, но и потенциально более доходными являются акции и облигации выпущенные не столь известными и не столь крупными компаниями. При этом, чем менее известна компания, тем большую прибыль она вынуждена обещать по своим облигациям (иначе никто не захочет их покупать) и тем сильнее могут в итоге «выстрелить» её акции. Ведь согласитесь, что у автосервиса за углом вашего дома, потенциал к возможному росту куда выше чем, например, у Газпрома или Сбербанка. Автосервис может увеличиться в тысячи раз развивая свой бизнес в сеть по всему городу, по всей стране или, в конце концов, даже по всему миру (вовсе не обязательно что он это сделает, но, тем не менее, теоретическая возможность этого ведь существует). А вот Газпром это уже и так достаточно крупная организация и вряд ли он сможет увеличить свою рыночную капитализацию даже в 5-10 раз.

Есть ещё такие бумаги как фьючерсные и опционные контракты. Торговля ими осуществляется с использованием кредитного плеча (левериджа) и, соответственно, размер потенциальной прибыли в данном случае гораздо выше, он прямо пропорционален размеру предоставляемого плеча. Аналогичным образом растёт и риск.

Предположим, что вы решили приобрести фьючерс на акции IBM. Спецификация данного фьючерсного контракта подразумевает его торговлю с размером левериджа 1 к 10. То есть, при цене одной акции в 135 долларов, обладая суммой в 1350$, вы можете приобрести не десять, а сто таких акций. Хотя если говорить точнее, в данном случае вы приобретёте не сами акции IBM, а фьючерсный контракт на их покупку. Но сути дела это сильно не меняет, ведь по истечении срока данного контракта вы сможете получить прибыль равнозначную той, которая была бы у вас при продаже этих самых акций. Правда при этом и возможный убыток будет равен тому, который вам принесло бы обладание 100 акциями IBM в случае снижения их курсовой стоимости.

Формулы расчёта доходности ценных бумаг

Вообще, доходность по ценным бумагам может складываться из следующих величин:

1. Спекулятивный доход получаемый в результате реализации курсовой разницы при покупке и продаже ценных бумаг;
2. Доход получаемый в виде дивидендов по акциям или в виде процентов по облигациям (купонный доход).

Кроме этого можно говорить о фактической и ожидаемой доходности инвестиций. Фактическая доходность отражает ту величину прибыли, которая была получена, что называется, постфактум. А ожидаемая — показывает ту её величину, которую можно будет получить в будущем.

Про ожидаемую доходность мы поговорим в следующем разделе, а сейчас давайте рассмотрим как рассчитывается фактическая доходность инвестиций в ценные бумаги.

Если речь идёт о чисто спекулятивной доходности (от разницы курсовой стоимости), то её легко можно рассчитать по формуле:

В том случае, если помимо курсовой разницы были получены ещё проценты или дивиденды, доход рассчитывается по формуле:

Обычно доходность рассчитывается в процентах годовых. Для того чтобы привести рассчитанные по вышеприведённым формулам результаты к годовой доходности, следует воспользоваться этой зависимостью:

Ожидаемая доходность ценных бумаг

Грамотное инвестирование в ценные бумаги, предполагает вероятностную оценку рисков и возможностей, выбор допускаемого значения риска и сопоставимого с ним потенциального уровня доходности**. Об инвестиционных рисках и о способах их минимизации мы говорили с вами здесь. А сейчас я расскажу вам о том, как оценить потенциальную доходность ценных бумаг.

Оценить ожидаемую доходность (ОД) можно двумя различными методами. Первый метод основан на вероятностях (математическом ожидании), а второй — на исторических данных. Давайте начнём с вероятностного метода оценки.

** Как мы уже говорили с вами выше, риск и доходность ценных бумаг находятся в прямо пропорциональной зависимости друг от друга. Чем выше риск, тем выше потенциальный уровень доходности и наоборот. Такое положение вещей обусловлено тем, что рынок сам устанавливает данное соотношение, ведь никто не хочет покупать высокорисковые бумаги с небольшим уровнем доходности.

Оценка доходности на основе математического ожидания

В данном случае учитываются все возможные варианты размера предполагаемой доходности вкупе с их вероятностью. Причём наибольший вес придаётся тем значениям, вероятность получения которых выше.

Расчёт производится по формуле:

Для наглядности вычислений, давайте приведём простой пример. Допустим перед инвестором встал выбор из двух бумаг со следующим распределением вероятностей прибылей по ним:

1. Бумага А предположительно принесёт доходность в 10% с вероятностью в 50%, доходность в 7% с вероятностью в 30% или доходность в 4% с вероятностью в 20%;
2. Бумага Б. Вероятность доходности в 12% составляет 30%, вероятность доходности в 8% составляет 35% и вероятность доходности в 5% составляет 35%.

Сначала рассчитываем ожидаемую доходность для бумаги А:

ОД = (0,1*0,5) + (0,07*0,3) + (0,04*0,2) = 0,079 = 7,9%

А теперь рассчитаем ожидаемую доходность для бумаги Б:

ОД = (0,12*0,3) + (0,08*0,35) + (0,05*0,35) = 0,081 = 8,1%

Очевидно, что фактическое значение доходности, скорее всего, будет несколько отличаться от рассчитанного по вышеприведённой формуле. Оценить разброс значений фактических, относительно значений расчётных, можно рассчитав величину дисперсии.

Дисперсия рассчитывается по формуле:

Для нашего примера получим дисперсию для бумаги А:

0,5(0,1 — 0,079) 2 + 0,3(0,07 — 0,079) 2 + 0,2(0,04 — 0,079) 2 = 0,000549

И дисперсию для бумаги Б:

0,3(0,12 — 0,081) 2 + 0,35(0,08 — 0,081) 2 + 0,35(0,05 — 0,081) 2 = 0,000793

Дисперсия показывает тот уровень риска, который повлечёт за собой инвестирование в бумагу для которой была рассчитана ожидаемая доходность на основе вероятностей (математического ожидания). Чем больше дисперсия, тем больше возможное отклонение фактического значения ОД от расчётного.

В нашем примере дисперсия для бумаги Б несколько выше аналогичного показателя для бумаги А. Однако, разница между ними совсем незначительная (не на порядок), поэтому можно считать, что риски рассматриваемых бумаг примерно равны. Следовательно, при прочих равных, инвестирование в бумагу Б является предпочтительным.

Оценка доходности на основе исторических данных

Как вы понимаете, не всегда есть возможность объективно оценить вероятности получения того или иного размера прибыли. Поэтому, на практике часто используют второй метод оценки ОД. Для второго способа расчёта ОД предполагается наличие данных по доходности за несколько равных временных периодов (например, за несколько лет).

Расчёт производится по следующей формуле:

Для примера, давайте опять сравним акции двух компаний А и Б. Для простоты примера возьмём статистику годовой доходности за три последних года. Пускай акции компании А приносили доход в размере:

1. Первый год — 10%;
2. Второй год — 8%;
3. Трети год — 15%.

А акции компании Б:

1. Первый год — 5%;
2. Второй год — 15%;
3. Третий год — 10%.

Подставляя эти значения в формулу получим, для акций компании А:

Для акций компании Б:

Как видите, согласно расчёту, акции компании Б оказываются чуть более выгодными. Однако следует иметь ввиду, что значения доходности в прошлом, не гарантируют её в будущем. Так, в данном примере, на третий год произошло некоторое снижение прибыли. Это может быть вызвано как временными, но преодолимыми трудностями (вызванными, например, изменением конъюнктуры на рынках сбыта), так и свидетельствовать о более серьёзных проблемах компании (наличие которых, скорее всего, повлечёт за собой дальнейшее снижение прибыльности её бумаг).

Источник