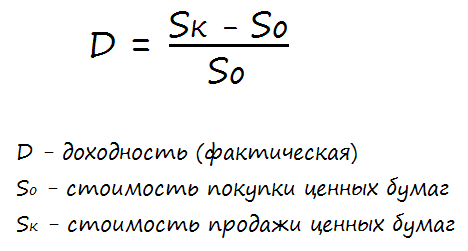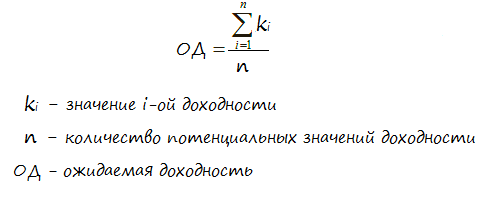Математическое ожидание доходности финансовых операций

Анализ доходности и риска финансовых операций на основе принципа оптимальности Парето

Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку, цель проведения которой заключается в максимизации дохода — разности между конечной и начальной оценками.

Обычно финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль, так и убыток (или незначительная прибыль по сравнению с ожидаемой).

Существует несколько способов оценки финансовой операции с точки зрения ее доходности и риска. Наиболее часто доход операции представляется случайной величиной Q, а риск операции r оценивается средним квадратическим отклонением этого случайного дохода.

Постановка задачи в общем виде. Пусть А – некоторое множество операций, которые различаются хо­тя бы одной характеристикой. При выборе наилучшей опе­рации желательно, чтобы Q было больше, а r меньше.

Считают, что операция а доминирует операцию b (обозначается а > b), если Q (а) ≥ Q (b) и r(a) ≤ r(b) и хотя бы одно из этих неравенств строгое. При этом операция а называется доминирующей, а операция b – доминируемой. Причем никакая доминируемая операция не может быть признана наилучшей, поэтому наилучшую операцию следует искать среди недоминируемых операций. Множество недоминируемых операций называется множеством (областью) Парето или множеством оптимальности по Парето[4].

Для множества Парето справедливо утверждение: каждая из характе­ристик Q, r является однозначной функцией другой, т.е. на множестве Парето по од­ной характеристике операции можно однозначно определить другую.

Пример. 3.8. Из четырех возможных финансовых операций с ожидаемыми доходностями Q₁, Q₂, Q₃, Q₄ и соответствующими вероятностями их получения p₁, p₂, p₃ , p₄ необходимо выбрать операцию оптимальную по Парето.

Значения ожидаемых доходностей q_j и соответствующих им вероятностей p_j приведены в следующей матрице

Поскольку ожидаемый доход финансовой операции считается случайной величиной Q, то его среднее значение оценивают математическим ожиданием: 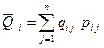, (3.16)

где p_{i j} — вероятность получения дохода q_{i j} в i – ой финансовой операции.

Количественной мерой риска r финансовой операции считается s — среднее квадратическое отклонение

r _i = 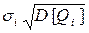, (3.17)

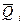
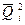
которое характеризует степень разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Дисперсию доходности D[Qi] удобно оценивать по формуле: D[Q i] = M [(Q i — ) 2 ] = M [Q _i 2 ] – [ ] .

Здесь M [Q _i 2 ] = å q 2 _{i j} p_{i j} – математическое ожидание квадрата ожидаемой доходности в i-ой финансовой операции.

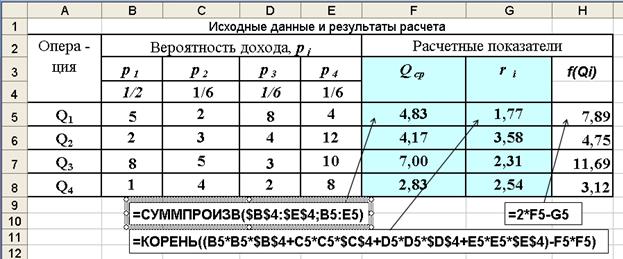
Расчеты средних ожидаемых доходов и рисков по вышеприведенным формулам выполним в среде Excel. Рабочий лист с исходными данными, расчетными формулами и результатами расчета средних доходностей Q _{c p} и риска r приведен на рис. 3.14.

Рис. 3.14. Общий вид рабочего листа с результатами расчета

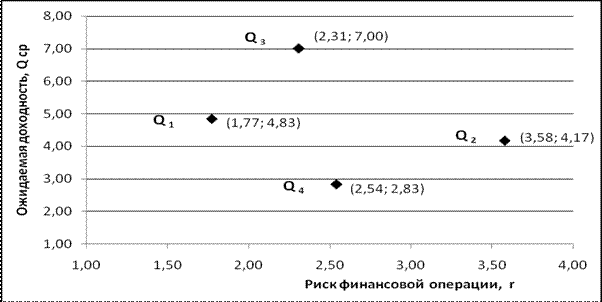
Найденные в результате расчета средние ожидаемые доходы`Q_i и соответствующие им риски r_i нанесем на график в системе координат: доход (вертикальная ось) — риски (горизонтальная ось), рис. 3.15.

Рис. 3.15. Графическая интерпретация результатов расчета эффективности финансовых операций в системе координат: ожидаемая доходность – риск

Проанализируем взаимное расположение 4-х точек на графике с позиции их доминирования. Чем выше точка (`Q, r), тем более доходная операция, чем точка правее — тем операция более рисковая. Значит, нужно выбирать точку выше и левее. Точка (`Q¢, r¢) доминирует точку (`Q, r) если `Q¢ ³`Q и r¢ £ r. В данном случае 1-я операция доминирует 2-ю, 3-я доминирует 2-ю и 3-я доминирует 4-ю. Но 1-я и 3-я операции несравнимы — доходность 3-й больше, но и риск ее тоже больше.

Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Выбор лучшей из рассматриваемых операций производится обязательно из операций, оптимальных по Парето.

Для нахождения лучшей операции иногда применяют взвешивающую формулу, которая для пар (`Q, r) дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула имеет вид:

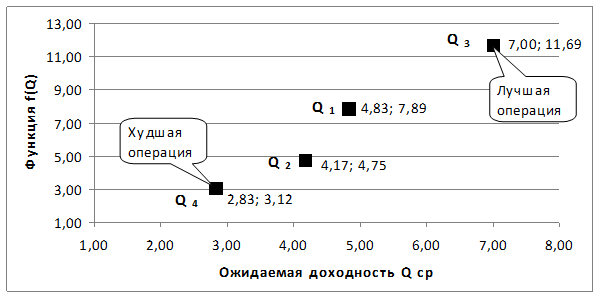
На рис. 3.16. приведена графическая иллюстрация результатов, полученных с помощью взвешивающей формулы.

Рис.3.16. Множество операций

Из последнего рисунка видно, что 3-я операция – лучшая, расположена в правом верхнем углу графика, а 4-я – худшая занимает левый нижний угол.

3.6. Экспертные методы оценки риска

Когда из-за отсутствия данных, нельзя использовать количественные методы прогнозирования показателей риска, могут использоваться экспертные методы оценки риска. Задача экспертного оценивания сводится к получению группового субъективного мнения на основе обработки совокупности индивидуальных мнений экспертов.

Методы экспертной оценки риска – совокупность логических и математических процедур позволяющих получать информацию от специалистов-экспертов, проводить ее анализ и обобщать результаты для выбора рациональных решений.

Среди методов экспертных оценок выделяются две группы: коллективные методы оценивания и методы получения индивидуального мнения экспертов.

Коллективные методы оценивания («мозговая атака», деловые игры, сценарии, совещания, «суд») предполагают выработку общего мнения в ходе совместного обсуждения.

Методы получения индивидуального мнения (анкетный опрос, Дельфи, интервью) построены на предварительном сборе информации от опрашиваемых индивидуально экспертов.

Применение экспертных методов оценки риска связано с реализацией следующих этапов:

— определение цели и задач экспертного оценивания;

— формирование рабочей группы для управления и проведения экспертного оценивания;

— выбор метода получения экспертной информации и способов ее обработки;

— формирование группы экспертов и разработка анкет опроса;

— опрос экспертов (проведение экспертизы);

— обработка и анализ результатов экспертизы;

— интерпретация полученных результатов;

На первом этапе определения цели экспертизы устанавливается признак, по которому производится оценка. Если целей несколько, то оценки по различным шкалам целесообразно свести к единой шкале, например за счет установления цели более высокого уровня.

Методы групповой экспертной оценки делятся на два вида: открытая дискуссия и анкетный опрос.

Метод открытой дискуссии имеет ряд недостатков: не исключается давление авторитетов, затруднена математическая обработка обобщенного мнения группы экспертов и степени их согласованности.

Опрос экспертов с помощью анкет устраняет недостатки методов открытой дискуссии, поскольку свои заключения по поставленным вопросам эксперты представляют анонимно.

Формирование группы экспертов связано с вопросами определения ее качественного и количественного состава.

При качественном отборе к экспертам предъявляются следующие требования: информированность, высокий уровень общей эрудиции, отсутствие личной заинтересованности в результатах экспертизы, глубокие специальные знания в оцениваемой области деловитость и объективность, наличие производственного и (или) исследовательского опыта в данной области и т.д.

Степень компетентности экспертов оценивается одним из двух способов: объективный способ; субъективный способ.

Наиболее часто пользуются субъективными способами, которые в свою очередь делятся на два вида:

взаимооценочные – уровень компетентности экспертов определяется по характеристикам, данных им другими участниками экспертизы;

самооценочные – сам эксперт определяет вес своей оценки по некоторому вопросу, пользуясь оценочной шкалой, представляемой ему прогнозистом.

Второй способ определения компетентности экспертов более простой с точки зрения получения исходных данных, поскольку не требует предварительной обработки данных для получения веса оценки эксперта.

Компетентность эксперта (К) оценивается степенью его квалификации, которая определяется на основе суждений эксперта о своей информированности по решаемой проблеме (Ки) и уровне аргументации своих мнений (Ка): К = 0,5 (Ки + Ка).

Увеличение количества экспертов приводит к снижению погрешности экспертной оценки, но при этом точность прогноза растет медленнее количества экспертов. На практике подбирается компромиссный вариант между требуемой точностью и стоимостью прогноза. Считается, что в состав группы целесообразно включать не менее 5-12 специалистов.

На точность групповых оценок также влияет и степень согласованности ответов экспертов.

Вопросы для экспертов, могут иметь содержательный ответ в развернутой форме или в виде количественной оценки.

В последнем случае возможно применение математических методов обработки результатов.

Метод «Дельфи» реализует анкетный способ опроса при прогнозировании количественных показателей. Для повышения достоверности групповой оценки экспертиза проводится в 3-4 тура. После каждого тура экспертов знакомят с результатами прежнего тура перед началом следующего.

Доверительная вероятность такого прогноза составляет 50%.

Источник

Курс лекций «Основы финансового менеджмента»

5.5. Количественное измерение риска

Средняя арифметическая ожидаемых доходностей ( r i ) инвестиций, взвешенная по вероятности возникновения отдельных значений, называется математическим ожиданием. Условимся называть эту величину средней ожидаемой доходностью :

, (5.5.1)

где p i – вероятность получения доходности r i .

В статистике количественным измерителем степени разброса значений переменной вокруг ее средней величины (математического ожидания) является показатель дисперсии ( σ 2 ):

(5.5.2)

Квадратный корень из дисперсии называется средним квадратическим или стандартным отклонением σ :

(5.5.3)

Данный показатель используется в финансовом менеджменте для количественного измерения степени риска планируемых инвестиций. Чем больше разброс ожидаемых значений доходности вложений вокруг их среднеарифметической величины, тем выше риск, сопряженный с данным вложением . Фактическая величина доходности может быть как значительно выше, так и значительно ниже ее средней величины.

Практическая ценность такого подхода заключается не только (и не столько) в применении статистических формул, а в осознании необходимости многовариантного планирования инвестиционных решений. Любые ожидаемые результаты этих решений могут носить лишь вероятностный характер. От финансиста требуется не только правильно применить формулу расчета доходности инвестиций, но и дать количественную оценку вероятности возникновения конкретного результата. Как минимум, необходимо планировать не менее трех вариантов развития событий : оптимистический, пессимистический и наиболее вероятный. Полная вероятность возникновения всех этих вариантов должна быть равна 1.

Например, оценивая две акции А и Б, инвестор пришел к выводу, что распределение вероятностей их ожидаемой доходности можно представить следующим образом:

Источник

Доходность ценных бумаг. Основные методы оценки и прогнозирования

Ни для кого не секрет, что основной целью инвестиций в ценные бумаги является получение максимально возможной прибыли при сохранении приемлемого уровня риска. В этой статье я расскажу вам о том, какие виды ценных бумаг обладают потенциально большим потенциалом доходности. Вы узнаете о том из чего складывается их доходность и каким образом она вычисляется. Наконец, мы с вами подробно поговорим о том, как можно провести предварительную оценку и рассчитать ожидаемую доходность ценных бумаг ещё на этапе их выбора.

Какие бумаги потенциально самые прибыльные

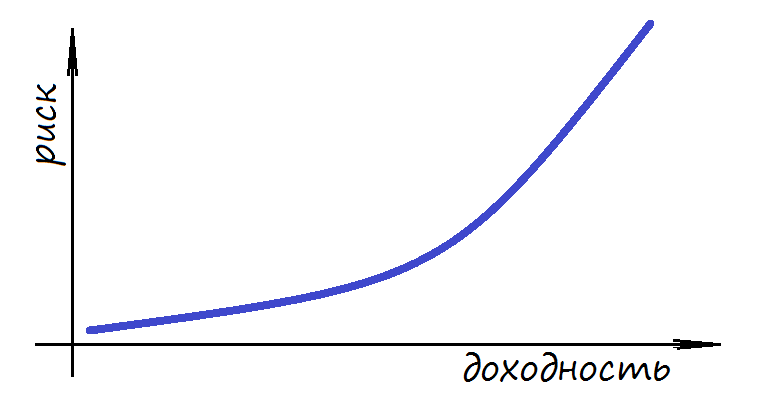
Ответ на этот вопрос довольно прост: самый большой потенциал в плане прибыли имеют ценные бумаги с таким же большим уровнем риска. Чем выше риск, который готов взять на себя инвестор, тем выше тот доход, который он может в итоге получить. Ключевое слово в данном случае – «может», поскольку с увеличением степени риска вероятность получения дохода постепенно тает.

Соотношение риска и доходности

То есть, другими словами, увеличивая степень риска инвестор одновременно и повышает свою потенциальную доходность, и снижает вероятность её получения. Поэтому в инвестициях так важно найти ту самую золотую середину, тот уровень риска при котором можно рассчитывать на относительно высокую прибыль с достаточно большой вероятностью её получения.

Минимальным риском, но и наименьшей степенью доходности отличаются такие бумаги, как государственные облигации. Обычно процент по ним сопоставим с доходностью банковских депозитов и едва превышает текущий уровень инфляции. Инвестирование в бумаги данного типа целесообразно в тех случаях, когда основной целью является не приумножение, а сохранение своих денежных средств.

На ступеньку выше стоят корпоративные облигации крупнейших компаний. Они также обладают достаточной степенью надёжности, но позволяют получить чуть большую прибыль (в отличие от бумаг выпущенных государством). Ещё выше по доходности – акции тех же самых компаний, но и риск по ним тоже чуть выше. Облигация по природе своей — долговая ценная бумага, то есть она подразумевает возврат долга и процентов по нему в любом случае. А вот акция — бумага долевая. Она даёт своему владельцу долю в бизнесе компании её выпустившей, но вместе с этим он принимает на себя и определённые риски (в частности, убытки в результате возможного снижения курса акций).

Ещё более рисковыми, но и потенциально более доходными являются акции и облигации выпущенные не столь известными и не столь крупными компаниями. При этом, чем менее известна компания, тем большую прибыль она вынуждена обещать по своим облигациям (иначе никто не захочет их покупать) и тем сильнее могут в итоге «выстрелить» её акции. Ведь согласитесь, что у автосервиса за углом вашего дома, потенциал к возможному росту куда выше чем, например, у Газпрома или Сбербанка. Автосервис может увеличиться в тысячи раз развивая свой бизнес в сеть по всему городу, по всей стране или, в конце концов, даже по всему миру (вовсе не обязательно что он это сделает, но, тем не менее, теоретическая возможность этого ведь существует). А вот Газпром это уже и так достаточно крупная организация и вряд ли он сможет увеличить свою рыночную капитализацию даже в 5-10 раз.

Есть ещё такие бумаги как фьючерсные и опционные контракты. Торговля ими осуществляется с использованием кредитного плеча (левериджа) и, соответственно, размер потенциальной прибыли в данном случае гораздо выше, он прямо пропорционален размеру предоставляемого плеча. Аналогичным образом растёт и риск.

Предположим, что вы решили приобрести фьючерс на акции IBM. Спецификация данного фьючерсного контракта подразумевает его торговлю с размером левериджа 1 к 10. То есть, при цене одной акции в 135 долларов, обладая суммой в 1350$, вы можете приобрести не десять, а сто таких акций. Хотя если говорить точнее, в данном случае вы приобретёте не сами акции IBM, а фьючерсный контракт на их покупку. Но сути дела это сильно не меняет, ведь по истечении срока данного контракта вы сможете получить прибыль равнозначную той, которая была бы у вас при продаже этих самых акций. Правда при этом и возможный убыток будет равен тому, который вам принесло бы обладание 100 акциями IBM в случае снижения их курсовой стоимости.

Формулы расчёта доходности ценных бумаг

Вообще, доходность по ценным бумагам может складываться из следующих величин:

1. Спекулятивный доход получаемый в результате реализации курсовой разницы при покупке и продаже ценных бумаг;
2. Доход получаемый в виде дивидендов по акциям или в виде процентов по облигациям (купонный доход).

Кроме этого можно говорить о фактической и ожидаемой доходности инвестиций. Фактическая доходность отражает ту величину прибыли, которая была получена, что называется, постфактум. А ожидаемая — показывает ту её величину, которую можно будет получить в будущем.

Про ожидаемую доходность мы поговорим в следующем разделе, а сейчас давайте рассмотрим как рассчитывается фактическая доходность инвестиций в ценные бумаги.

Если речь идёт о чисто спекулятивной доходности (от разницы курсовой стоимости), то её легко можно рассчитать по формуле:

В том случае, если помимо курсовой разницы были получены ещё проценты или дивиденды, доход рассчитывается по формуле:

Обычно доходность рассчитывается в процентах годовых. Для того чтобы привести рассчитанные по вышеприведённым формулам результаты к годовой доходности, следует воспользоваться этой зависимостью:

Ожидаемая доходность ценных бумаг

Грамотное инвестирование в ценные бумаги, предполагает вероятностную оценку рисков и возможностей, выбор допускаемого значения риска и сопоставимого с ним потенциального уровня доходности**. Об инвестиционных рисках и о способах их минимизации мы говорили с вами здесь. А сейчас я расскажу вам о том, как оценить потенциальную доходность ценных бумаг.

Оценить ожидаемую доходность (ОД) можно двумя различными методами. Первый метод основан на вероятностях (математическом ожидании), а второй — на исторических данных. Давайте начнём с вероятностного метода оценки.

** Как мы уже говорили с вами выше, риск и доходность ценных бумаг находятся в прямо пропорциональной зависимости друг от друга. Чем выше риск, тем выше потенциальный уровень доходности и наоборот. Такое положение вещей обусловлено тем, что рынок сам устанавливает данное соотношение, ведь никто не хочет покупать высокорисковые бумаги с небольшим уровнем доходности.

Оценка доходности на основе математического ожидания

В данном случае учитываются все возможные варианты размера предполагаемой доходности вкупе с их вероятностью. Причём наибольший вес придаётся тем значениям, вероятность получения которых выше.

Расчёт производится по формуле:

Для наглядности вычислений, давайте приведём простой пример. Допустим перед инвестором встал выбор из двух бумаг со следующим распределением вероятностей прибылей по ним:

1. Бумага А предположительно принесёт доходность в 10% с вероятностью в 50%, доходность в 7% с вероятностью в 30% или доходность в 4% с вероятностью в 20%;
2. Бумага Б. Вероятность доходности в 12% составляет 30%, вероятность доходности в 8% составляет 35% и вероятность доходности в 5% составляет 35%.

Сначала рассчитываем ожидаемую доходность для бумаги А:

ОД = (0,1*0,5) + (0,07*0,3) + (0,04*0,2) = 0,079 = 7,9%

А теперь рассчитаем ожидаемую доходность для бумаги Б:

ОД = (0,12*0,3) + (0,08*0,35) + (0,05*0,35) = 0,081 = 8,1%

Очевидно, что фактическое значение доходности, скорее всего, будет несколько отличаться от рассчитанного по вышеприведённой формуле. Оценить разброс значений фактических, относительно значений расчётных, можно рассчитав величину дисперсии.

Дисперсия рассчитывается по формуле:

Для нашего примера получим дисперсию для бумаги А:

0,5(0,1 — 0,079) 2 + 0,3(0,07 — 0,079) 2 + 0,2(0,04 — 0,079) 2 = 0,000549

И дисперсию для бумаги Б:

0,3(0,12 — 0,081) 2 + 0,35(0,08 — 0,081) 2 + 0,35(0,05 — 0,081) 2 = 0,000793

Дисперсия показывает тот уровень риска, который повлечёт за собой инвестирование в бумагу для которой была рассчитана ожидаемая доходность на основе вероятностей (математического ожидания). Чем больше дисперсия, тем больше возможное отклонение фактического значения ОД от расчётного.

В нашем примере дисперсия для бумаги Б несколько выше аналогичного показателя для бумаги А. Однако, разница между ними совсем незначительная (не на порядок), поэтому можно считать, что риски рассматриваемых бумаг примерно равны. Следовательно, при прочих равных, инвестирование в бумагу Б является предпочтительным.

Оценка доходности на основе исторических данных

Как вы понимаете, не всегда есть возможность объективно оценить вероятности получения того или иного размера прибыли. Поэтому, на практике часто используют второй метод оценки ОД. Для второго способа расчёта ОД предполагается наличие данных по доходности за несколько равных временных периодов (например, за несколько лет).

Расчёт производится по следующей формуле:

Для примера, давайте опять сравним акции двух компаний А и Б. Для простоты примера возьмём статистику годовой доходности за три последних года. Пускай акции компании А приносили доход в размере:

1. Первый год — 10%;
2. Второй год — 8%;
3. Трети год — 15%.

А акции компании Б:

1. Первый год — 5%;
2. Второй год — 15%;
3. Третий год — 10%.

Подставляя эти значения в формулу получим, для акций компании А:

Для акций компании Б:

Как видите, согласно расчёту, акции компании Б оказываются чуть более выгодными. Однако следует иметь ввиду, что значения доходности в прошлом, не гарантируют её в будущем. Так, в данном примере, на третий год произошло некоторое снижение прибыли. Это может быть вызвано как временными, но преодолимыми трудностями (вызванными, например, изменением конъюнктуры на рынках сбыта), так и свидетельствовать о более серьёзных проблемах компании (наличие которых, скорее всего, повлечёт за собой дальнейшее снижение прибыльности её бумаг).

Источник