- Определение курсовой стоимости и доходности облигаций
- Доходность облигаций: простыми словами
- Какие виды дохода есть у облигаций?
- Что показывает ставка купона?
- Купонная доходность
- Купонная доходность — это проценты инвестора?
- Доходность упала — цена выросла. Это не шутка?
- Какая доходность будет при продаже облигации?
- Как получить максимальную выгоду от продажи?
- Что такое эффективная доходность к погашению?
- Wiki-Yango
Определение курсовой стоимости и доходности облигаций
Определение курсовой стоимости и доходности ценных бумаг
В настоящей главе рассматривается техника расчетов курсовой стоимости и доходности ценных бумаг. Вначале мы остановимся на определении курсовой стоимости и доходности облигаций. После этого перейдем к акциям, векселям и банковским сертификатам.
Определение курсовой стоимости облигаций.
Определение курсовой стоимости ценных бумаг основано на принципе дисконтирования, рассмотренного нами в главе 3. Инвестор приобретает ценную бумагу, чтобы получать доходы, которые она приносит. Поэтому для ответа на вопрос, сколько сегодня должна стоить та или иная ценная бумага, необходимо определить дисконтированную стоимость всех доходов, которые она принесет.
Технику определения курсовой стоимости можно представить в три действия. 1) Определяем поток доходов, который ожидается по ценной бумаге. 2) Находим дисконтированную (сегодняшнюю) стоимость величины каждого платежа по бумаге. 3) Суммируем дисконтированные стоимости. Данная сумма и представляет собой курсовую стоимость ценной бумаги.
После того как мы привели общий принцип расчета курсовой стоимости, рассмотрим определение курса различных видов облигаций.
Определение курсовой стоимости купонной облигации
Рассмотрим пример. Номинал облигации равен 1 млн. руб., купон — 20%, выплачивается один раз в год, до погашения остается три года. На рынке доходность на инвестиции с уровнем риска, соответствующим данной облигации, оценивается в 25%. Определить курсовую стоимость бумаги.
Определяем поток доходов, который принесет облигация инвестору за три года. В конце каждого года инвестор получит купон в сумме 200 тыс. руб., и в конце третьего года ему выплатят сумму номинала в размере 1 млн. руб. Таким образом, облигация принесет следующий поток доходов.
Определяем дисконтированную стоимость суммы каждого платежа по облигации. Для первого платежа она равна:
где: Р — цена облигации,
п — число лет до погашения облигации;
r — доходность до погашения облигации. 1
В формуле (62) важно отметить, что п — это количество лет, которые остаются до погашения бумаги. Например, облигация выпущена на 10 лет, однако 7 лет уже прошло. Определяя курсовую стоимость такой бумаги следует взять п равной трем. Это вытекает из принципа дисконтирования будущих доходов. В данном случае облигация принесет доходы инвестору только за три оставшиеся года.
В формуле (62) появилось такое понятие как доходность до погашения (или доходность к погашению). Доходность до погашения — это доходность в расчете на год, которую обеспечит себе инвестор, если, купив облигацию, продержит ее до погашения. В нашем примере, заплатив за облигацию 902400 руб., вкладчик обеспечил себе ежегодную доходность из расчета 25% годовых. Если владелец облигации продаст ее до момента погашения, то, как правило, он не получит данного уровня доходности, так как конечный результат его операции будет зависеть от цены продажи облигации на рынке.
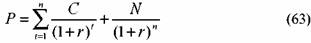
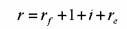
rf — ставка без риска, т. е. ставка по инвестициям, для которых отсутствует риск; в качестве такой ставки берут доходность по государственным ценным бумагам для соответствующих сроков погашения,
l — премия за ликвидность,
i— темп инфляции,
re — реальная ставка процента.
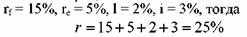
Поэтому данная величина должна найти отражение в ставке дисконтирования.
Ставку дисконтирования также можно определить аналитически, о чем будет сказано в главе, посвященной управлению портфелем ценных бумаг.
Рассмотрим еще один пример. N = 1млн. руб., купон — 20%, доходность до погашения — 15%, до погашения остается три года.
Цена облигации равна:
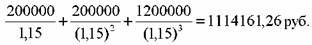
Между курсовой стоимостью и доходностью до погашения облигации существуют следующие зависимости.
Цена облигации и доходность до погашения находятся в обратной связи. При повышении доходности цена облигации падает, при понижении — возрастает.
Если доходность до погашения выше купонного процента, облигация продается со скидкой.
Если доходность до погашения ниже купонного процента, облигация продается с премией.
Если доходность до погашения равна купонному проценту, цена облигации равна номиналу.
При понижении доходности до погашения на 1° о цена облигации возрастает в большей степени в сравнении с ее падением при увеличении доходности до погашения на 1%.
Как уже отмечалось, котировки облигаций приводятся в процентах к номинальной стоимости. Поэтому при определении курсовой стоимости облигации можно пользоваться не величинами в денежном выражении, а в процентах. В этом случае номинал принимается за 100%. В качестве иллюстрации запишем приведенный выше пример с использованием процентов:

Купон по облигации может выплачиваться чаще, чем один раз в год. В таком случае формула (63) примет вид:
где: т — частота выплаты купона в течение года.
Как видно из формулы (64), количество слагаемых увеличивается в т раз. Дополним наш последний пример условием, что купон выплачивается два раза в год, и найдем цену облигации:
Формулы (63) и (64) можно привести к более удобному виду, учитывая тот факт, что выплата купонов представляет собой не что иное как аннуитет:
Приведенные формулы позволяют рассчитать чистую цену облигации, т. е. цену на основе целых купонных периодов. Однако бумаги продаются и покупаются также в ходе купонного периода. Поэтому следует ответить на вопрос, каким образом рассчитать полную цену облигации, т. е. цену, скорректированную на размер накопленных к моменту сделки суммы купонных процентов. Общий подход и в данном случае остается прежним, т. е. необходимо дисконтировать будущие доходы с учетом времени, которое остается до их получения.
N = 100 тыс. руб., r = 20%, купон равен 10% и выплачивается один раз в год. До погашения облигации остается 2 года 345 дней. Определить цену облигации.
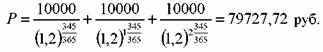
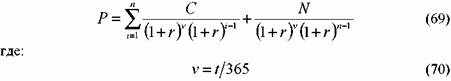
п — целое число лет, которое остается до погашения облигации, включая текущий год.
Если купон выплачивается т раз в год, то число купонных периодов в формуле (69) корректируется на т, как было показано выше, а в знаменателе формулы (69) вместо 365 дней указывается число дней в купонном периоде.
1. 1. 2. Определение курсовой стоимости среднесрочной и долгосрочной бескупонных облигаций.
Формулу определения курсовой стоимости бескупонной облигации можно получить из формулы (69). Поскольку по облигации не выплачиваются купоны, то С = 0 и формула (69) принимает вид:
N = 10000 руб., r = 20%, п = 3 года. Определить Р.
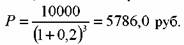
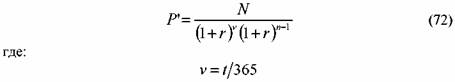
п — целое число лет, которое остается до погашения облигации, включая текущий год.
На практике приходится сравнивать купонные и бескупонные облигации. В этом случае необходимо помнить о следующем правиле. Если по купонным облигациям процент выплачивается т раз в год, то формулу (71) следует также скорректировать на т, а именно:

5. 1. 1. 3. Определение курсовой стоимости ГКО Цена ГКО определяется по формуле:

N = 1 млн. руб., t = 60 дней, r = 15%. Определить цену ГКО. Она равна:
5. 1. 1. 4. Определение курсовой стоимости ОФЗПК и ОГСЗ
Цена данных облигаций определяется стандартным способом, т. е. будущие доходы по облигациям дисконтируются к сегодняшнему дню и суммируются. Особенностью ОФЗ-ПК и ОГСЗ является то, что купоны у них плавающие и их величина изменяется в зависимости от ситуации на рынке ГКО. Поэтому инвестору необходимо вначале сделать прогноз относительно ситуации на рынке ГКО. Затем оценить величину будущих купонов и дисконтировать их и номинал к сегодняшнему дню.
Мы рассмотрели формулы определения курсовой стоимости облигаций. Они позволяют инвестору рассчитать приемлемый для него уровень цены бумаги. В то же время это не означает, что облигации на рынке обязательно будут продаваться по найденной цене. Так происходит потому, что различные вкладчики поразному могут оценивать риск приобретения облигации, и, следовательно, использовать несколько отличные ставки дисконтирования. Кроме того, на цену будут также влиять силы спроса и предложения. Если спрос превышает предложение, то это создаст потенциал к повышению цены, если предложение больше спроса, то — то к понижению.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Доходность облигаций: простыми словами
3 вида дохода, которые превратят обычного вкладчика в успешного рантье
Чего бы вы хотели достичь, инвестируя в облигации? Сохранить деньги и получить дополнительный доход? Сделать накопления для важной цели? А, может, мечтаете о том, как с помощью этих инвестиций получить финансовую свободу? Какой бы ни была цель, стоит понимать, какой доход приносят ваши облигации, и уметь отличить хорошую инвестицию от плохой. Есть несколько принципов для оценки дохода, знание которых в этом поможет.
Какие виды дохода есть у облигаций?
Доходность облигации — это величина дохода в процентах, полученного инвестором от вложений в долговую бумагу. Процентный доход по ним формируется за счет двух источников. С одной стороны, у облигаций с фиксированным купоном , как у депозитов, есть процентная ставка, которая начисляется на номинал. С другой стороны, у облигаций, как у акций, есть цена , которая может меняться в зависимости от рыночных факторов и ситуации в компании. Правда, изменения в цене у облигаций менее значимые, чем у акций.
Полная доходность облигации включает купонную доходность и учитывает цену ее приобретения. На практике для разных целей используют разные оценки доходности. Одни из них показывают только доходность от купона, другие дополнительно учитывают цену купли-продажи, третьи показывают рентабельность инвестиций в зависимости от срока владения — до продажи на рынке или до выкупа эмитентом , выпустившем облигацию.
Для принятия правильных инвестиционных решений, необходимо разобраться: какие виды доходности по облигациям бывают и что они показывают. Всего есть три вида доходности, управление которыми превращает обычного вкладчика в успешного рантье. Это текущая доходность от процентов по купонам, доходность при продаже и доходность бумаг к погашению.
Что показывает ставка купона?
Ставка купона — базовый процент к номиналу облигации, который также называют купонной доходностью . Эту ставку эмитент объявляет заранее и периодически выплачивает в установленный срок. Купонный период большинства российских облигаций — полгода или квартал. Важный нюанс заключается в том, что купонная доходность по облигации начисляется ежедневно, и инвестор не потеряет ее, даже если продаст бумагу досрочно.
Если сделка купли-продажи облигации происходит внутри купонного периода, то покупатель уплачивает продавцу сумму процентов, накопленных с даты последней выплаты купона. Сумма этих процентов называется накопленный купонный доход ( НКД ) и прибавляется к текущей рыночной цене облигации. По окончании купонного периода покупатель получит купон целиком и таким образом компенсирует свои расходы, связанные с возмещением НКД предыдущему владельцу облигации.
Биржевые котировки облигаций у многих брокеров показывают так называемую чистую цену облигации, без учета НКД. Однако когда инвестор даст поручение на покупку, к чистой цене прибавится НКД, и стоимость облигации внезапно может оказаться больше ожидаемой.
При сравнении котировок облигаций в торговых системах, интернет-магазинах и приложениях разных брокеров выясните, какую цену они указывают: чистую или с НКД. После этого оцените конечные затраты на покупку в той или иной брокерской компании, с учетом всех издержек, и узнайте, сколько денег у вас спишут со счета в случае покупки бумаг.
Купонная доходность
По мере роста накопленной купонной доходности (НКД) стоимость облигации растет. После выплаты купона стоимость уменьшается на сумму НКД.
НКД — накопленный купонный доход
С (coupon) — сумма купонных выплат за год, в рублях
t (time) — количество дней с начала купонного периода
Пример: инвестор купил облигацию номиналом 1000 ₽ со ставкой полугодового купона 8% в год, что означает выплату 80 ₽ в год, сделка прошла в 90-й день купонного периода. Его доплата предыдущему владельцу: НКД = 80 * 90 / 365 = 19,7 ₽
Купонная доходность — это проценты инвестора?
Не совсем. Каждый купонный период инвестор получает сумму определенных процентов по отношению к номиналу облигации на тот счет, который он указал при заключении договора с брокером. Однако реальный процент, который при этом получает инвестор на вложенные средства, зависит от цены приобретения облигации.
Если цена покупки была выше или ниже номинала, то доходность будет отличаться от базовой ставки купона, установленной эмитентом по отношению к номинальной стоимости облигации. Самый простой способ оценить реальный доход от вложения — соотнести ставку купона с ценой приобретения облигации по формуле текущей доходности.
Из представленных расчетов по этой формуле видно, что доходность и цена связаны между собой обратной пропорциональностью. Инвестор получает более низкую доходность к погашению, чем была установлена по купону, когда покупает облигацию по цене дороже номинала.
CY (current yield) — текущая доходность, от купона
Cг (coupon) — купонные выплаты за год, в рублях
P (price) — цена приобретения облигации
Пример: инвестор купил облигацию с номиналом 1000 ₽ по цене чистой 1050 ₽ или 105% от номинала и ставкой купона 8%, то есть 80 ₽ в год. Текущая доходность: CY = ( 80 / 1050) * 100% = 7,6% годовых.
Доходность упала — цена выросла. Это не шутка?
Так и есть. Однако, для начинающих инвесторов, которые не очень четко понимают различие между доходностью к продаже и доходностью к погашению, это зачастую трудный момент. Если рассматривать облигации как портфель инвестиционных активов, то его доходность к продаже в случае роста цены, как и у акций, конечно же, вырастет. А вот доходность облигаций к погашению будет меняться иначе.
Все дело в том, что облигация – это долговое обязательство, сравнить которое можно с депозитом. В обоих случаях, при покупке облигации или размещении денег на депозит, инвестор фактически приобретает право на поток платежей с определенной доходностью к погашению.
Как известно, процентные ставки по вкладам растут для новых вкладчиков, когда деньги обесцениваются из-за инфляции. Так же доходность к погашению облигации всегда растет, когда ее цена падает. Верно и обратное: доходность к погашению падает, когда цена растет.
Новички, которые оценивают выгоду в облигациях на основе сравнения с акциями, могут прийти к еще одному ошибочному выводу. Например: когда цена облигации выросла, допустим, до 105% и стала больше номинала, то покупать ее не выгодно, ведь при погашении по основному долгу вернут только 100%.
На самом деле, важна не цена, а доходность облигации — ключевой параметр для оценки ее привлекательности. Участники рынка, когда торгуются за облигацию, договариваются только о ее доходности. Цена облигации — это производный параметр от доходности. Фактически он корректирует фиксированную ставку купона до уровня той ставки доходности, о которой договорились покупатель и продавец.
Как связаны доходность и цена облигации, смотрите в видеоролике Академии Хана — образовательном проекте, созданном на деньги Google и фонда Билла и Мелинды Гейтс.
Какая доходность будет при продаже облигации?
Текущая доходность показывает отношение купонных выплат к рыночной цене облигации. Этот показатель не учитывает доход инвестора от изменения ее цены при погашении или продаже. Чтобы оценить финансовый результат, нужно рассчитать простую доходность, которая включает дисконт или премию к номинальной стоимости при покупке:
Y (yield) — простая доходность к погашению / оферте
CY (current yield) — текущая доходность, от купона
N (nominal) — номинал облигации
P (price) — цена покупки
t (time) — время от покупки до погашения/продажи
365/t — множитель для перевода изменения цены в проценты годовых.
Пример 1: инвестор приобрел двухлетнюю облигацию номиналом 1000 ₽ по цене 1050 ₽ со ставкой купона 8% годовых и текущей доходностью от купона 7,6%. Простая доходность к погашению: Y1 = 7,6% + ((1000-1050)/1050) * 365/730 *100% = 5,2% годовых
Пример 2: эмитенту повысили рейтинг спустя 90 дней после покупки облигации, после чего цена бумаги выросла до 1070 ₽, поэтому инвестор решил ее продать. Заменим в формуле номинал облигации на цену ее продажи, а срок до погашения — на срок владения. Получим простую доходность к продаже: Y2 7,6% + ((1070-1050)/1050) * 365/90 *100% = 15,3% годовых
Пример 3: Покупатель облигации, проданной предыдущим инвестором, заплатил за нее 1070 ₽ — больше, чем она стоила 90 дней назад. Так как цена облигации выросла, простая доходность к погашению для нового инвестора будет уже не 5,2%, а меньше: Y3 = 7,5% + ((1000-1070)/1070) * 365/640 *100% = 3,7% годовых
В нашем примере цена облигации за 90 дней выросла на 1,9%. В пересчете на годовую доходность это составило уже серьезную прибавку к процентным выплатам по купону — 7,72% годовых. При относительно небольшом изменении цены, облигации на небольшом промежутке времени могут показывать резкий скачок прибыли для инвестора.
После продажи облигации инвестор в течение года, возможно, уже не получит такую же доходность в размере 1,9% за каждые три месяца. Тем не менее, доходность, пересчитанная в годовые проценты, — это важный показатель, характеризующий текущий денежный поток инвестора. C его помощью можно принимать решение о досрочной продаже облигации.
Рассмотрим обратную ситуацию: при росте доходности цена облигации немного снизилась. В этом случае инвестор при досрочной продаже может получить убыток. Однако текущая доходность от выплат по купону, как видно в приведенной формуле, с большой долей вероятности перекроет этот убыток, и тогда инвестор все равно будет в плюсе.
Наименьший риск потери вложенных средств при досрочной продаже имеют облигации надежных компаний с коротким сроком до погашения или выкупа по оферте . Сильные колебания по ним могут наблюдаться, как правило, только в периоды экономического кризиса. Однако, их курсовая стоимость достаточно быстро восстанавливается по мере улучшения ситуации в экономике или приближения даты погашения.
Сделки с более надежными облигациями означают меньшие риски для инвестора, но и доходность к погашению или оферте по ним будет ниже. Это общее правило соотношения риска и доходности, которое действует в том числе при купле-продаже облигаций.
Как получить максимальную выгоду от продажи?
Итак, при росте цены доходность облигации падает. Следовательно, чтобы получить максимальную выгоду от роста цены при досрочной продаже, нужно выбирать облигации, доходность по которым может снизиться больше всего. Такую динамику, как правило, показывают бумаги эмитентов, имеющих потенциал для улучшения своего финансового положения и повышения кредитных рейтингов.
Большие изменения в доходности и цене могут показывать также облигации с большим сроком до погашения. Иными словами, длинные облигации более волатильны. Все дело в том, что длинные облигации формируют для инвесторов денежный поток большего объема, который сильнее влияет на изменение цены. Как это происходит, проще всего проиллюстрировать на примере тех же вкладов.
Предположим, вкладчик год назад разместил деньги на депозит по ставке 10% годовых на три года. А сейчас банк принимает деньги на новые депозиты уже по 8%. Если бы наш вкладчик мог переуступить вклад, как облигацию, другому инвестору, то покупателю пришлось бы доплатить разницу в 2% за каждый оставшийся год действия договора вклада. Доплата в данном случае составила бы 2 г * 2% = 4% сверху к денежной сумме во вкладе. За купленную на тех же условиях облигацию цена выросла бы примерно до 104% от номинала. Чем больше срок — тем больше доплата за облигацию.
Таким образом, инвестор получит больше прибыли от продажи облигаций, если выберет длинные бумаги с фиксированным купоном , когда ставки в экономике снижаются. Если же процентные ставки, напротив, растут, то держать длинные облигации становится невыгодно. В этом случае лучше обратить внимание на бумаги с фиксированным купоном, имеющие короткий срок до погашения, или облигации с плавающей ставкой .
Что такое эффективная доходность к погашению?
Эффективная доходность к погашению — это полный доход инвестора от вложений в облигации с учетом реинвестирования купонов по ставке первоначальных вложений. Для оценки полной доходности к погашению облигации или ее выкупу по оферте используют стандартный инвестиционный показатель — ставку внутренней доходности денежного потока. Она показывает среднегодовую доходность на вложения с учетом выплат инвестору в разные периоды времени. Иными словами, это рентабельность инвестиций в облигации.
Самостоятельно рассчитать ориентировочную эффективную доходность можно по упрощенной формуле. Погрешность расчетов составит десятые доли процента. Точная доходность будет чуть выше, если цена покупки превысила номинал, и чуть меньше — если была ниже номинала.
YTMор (Yield to maturity) — доходность к погашению, ориентировочная
Cг (coupon) — сумма купонных выплат за год, в рублях
P (price) — текущая рыночная цена облигации
N (nominal) — номинал облигации
t (time) — лет до погашени
Пример 1: инвестор приобрел двухлетнюю облигацию номиналом 1000 по цене 1050 ₽ со ставкой купона 8% годовых. Ориентировочная эффективная доходность к погашению: YTM1 = ((1000 – 1050)/(730/365) + 80) / (1000 + 1050) / 2 * 100% = 5,4% годовых
Пример 2: эмитенту повысили рейтинг спустя 90 дней после покупки облигации, и ее цена выросла до 1070 ₽, после чего инвестор решил продать облигацию. Заменим в формуле номинал облигации на цену ее продажи, а срок до погашения — на срок владения. Получим ориентировочную эффективную доходность к продаже (horizon yield): HY2 = ((1070 – 1050)/(90/365) + 80) / (1000 + 1050) / 2 * 100% = 15,7% годовых
Пример 3: Покупатель облигации, проданной предыдущим инвестором, заплатил за нее 1070 ₽ — больше, чем она стоила 90 дней назад. Так как цена облигации выросла, эффективная доходность к погашению для нового инвестора будет уже не 5,4%, а меньше: YTM3 = ((1000 – 1070)/(640/365) + 80) / (1000 + 1050) / 2 * 100% = 3,9% годовых
Самый простой способ узнать эффективную доходность к погашению по конкретной облигации — воспользоваться облигационным калькулятором на сайте Rusbonds.ru. Точный расчет эффективной доходности можно получить также с помощью финансового калькулятора или программы «Exel» через специальную функцию «внутренняя ставка доходности» и ее разновидности (XIRR). Эти калькуляторы вычислят ставку эффективной доходности по формуле ниже. Она рассчитывается приближенно — методом автоматического подбора чисел.
Как узнать доходность облигации, смотрите в видеоролике Высшей школы экономики с профессором Николаем Берзоном.
✔ Ключевой параметр облигации — это ее доходность, цена — производный параметр от доходности.
✔ Когда доходность облигации падает, цена на нее растет. И наоборот: при росте доходности цена на облигацию падает.
✔ Сравнивать можно сопоставимые вещи. Например, чистую цену без учета НКД — с чистой ценой облигации, а полную цену с НКД — с полной. Это сравнение поможет принять решение при выборе брокера.
✔ Короткие одно-двухлетние облигации более стабильны и меньше зависят от колебаний на рынке: инвесторы могут дождаться даты погашения или выкупа эмитентом по оферте.
✔ Длинные облигации с фиксированным купоном при снижении ставок в экономике позволяют больше заработать на их продаже.
✔ Успешный рантье может получить в облигациях три вида дохода: от выплат по купонам, от изменения рыночной цены при продаже или от возмещения номинальной стоимости при погашении.
 Wiki-Yango
Wiki-Yango
Доходчивый словарь терминов и определений облигационного рынка. Справочная база для российских инвесторов, вкладчиков и рантье.
ЧИТАЙТЕ ТАКЖЕ:
Источник


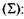
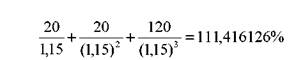
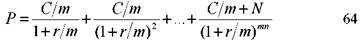
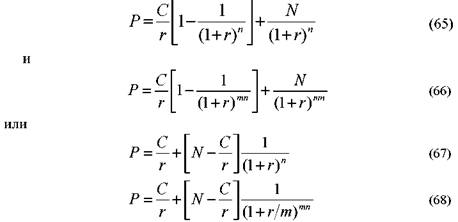

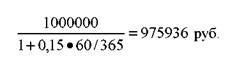







 Wiki-Yango
Wiki-Yango