Ковариация доходностей между двумя активами
3 Ковариация и корреляция.
Ковариация — это мера, учитывающая дисперсию индивидуальных значений доходности бумаги и силу связей между изменениями доходностей данной бумаги и других. Более простое определение ковариации — это мера взаимодействия двух случайных переменных.
Формула для расчета ковариации следующая:

где rx и ry – доходности активов X и Y,
rXсред и rYсред — ожидаемые (средние) доходности активов X и Y,
n – число наблюдений.
Интерпретация коэффициента следующая: положительное значение ковариации говорит о том, что значения доходности этих акций изменяются в одном направлении, отрицательное значение ковариации говорит о разнонаправленных движениях между доходностями. Ковариация является низкой, если колебания доходностей двух активов в любую сторону носят случайный характер.
Интерпретировать ковариацию, также как и дисперсию, довольно тяжело ввиду больших численных значений, поэтому практически всегда для измерения силы взаимосвязи между двумя активами используется коэффициент корреляции.
Коэффициент корреляции лежит в интервале от -1 до +1. Значение корреляции +1 говорит о сильной взаимосвязи, т.е. активы ходят одинаково. Значение -1, наоборот, свидетельствует о разнонаправленности, т.е. рост одного из активов сопровождается падением другого. Значение 0 говорит об отсутствии корреляции.
Расчет корреляции осуществляется по формуле:

где cov(X,Y) — ковариация между активами X и Y,
в знаменателе — стандартные отклонения активов X и Y
Приведем пример расчета ковариации и корреляции при помощи Excel между бумагами РАО ЕЭС, Лукойл и Ростелеком, пользуясь встроенными функциями КОВАР и КОРРЕЛ.
Рисунок 2.18 – Вид с формулами
В результате получим:
Рисунок 2.19 – Вид со значениями
Как видно из таблицы корреляции ежемесячные доходности наших активов на отрезке 2004 года являются положительно-коррелированы, что, конечно же, не очень хорошо, однако даже включение в портфель положительно-коррелированных активов способно существенно снизить риск всего портфеля. Вооружившись всеми теми данными, которые теперь есть можно спокойно переходить формированию портфеля и проблемам, связанными с этим.
Источник
Ковариация
Что такое Ковариация?
Ковариация измеряет направленную взаимосвязь между доходностью двух активов . Положительная ковариация означает, что доходность активов движется вместе, а отрицательная ковариация означает, что они движутся обратно. Ковариация рассчитывается путем анализа неожиданностей при доходности ( стандартных отклонений от ожидаемой доходности) или умножения корреляции между двумя переменными на стандартное отклонение каждой переменной.
Ключевые моменты
- Ковариация – это статистический инструмент, который используется для определения взаимосвязи между движением цен двух активов.
- Когда две акции имеют тенденцию двигаться вместе, они считаются имеющими положительную ковариацию; когда они движутся обратно, ковариация отрицательная.
- Ковариация – важный инструмент в современной теории портфеля, используемый для определения того, какие ценные бумаги следует поместить в портфель.
- Риск и волатильность портфеля можно снизить, объединив активы с отрицательной ковариацией.
Понимание ковариации
Ковариация оценивает, как средние значения двух переменных перемещаются вместе. Если доходность акции A увеличивается всякий раз, когда доходность акции B увеличивается, и такая же взаимосвязь обнаруживается, когда доходность каждой акции уменьшается, то считается, что эти акции имеют положительную ковариацию. В финансах ковариации рассчитываются, чтобы помочь диверсифицировать ценные бумаги.
Когда у аналитика есть набор данных, пара значений x и y, ковариация может быть рассчитана с использованием пяти переменных из этих данных. Они есть:
- x i = заданное значение x в наборе данных
- x m = среднее или среднее значение x
- y i = значение y в наборе данных, которое соответствует x i
- y m = среднее или среднее значение y
- n = количество точек данных
Учитывая эту информацию, формула ковариации: Cov (x, y) = SUM [(x i – x m ) * (y i – y m )] / (n – 1)
Краткая справка
Хотя ковариация действительно измеряет направленную взаимосвязь между двумя активами, она не показывает силу взаимосвязи между двумя активами; коэффициент корреляции является более подходящим показателем этой силы.
Ковариационные приложения
Ковариации имеют важное применение в финансах и современной теории портфелей . Например, в модели ценообразования капитальных активов ( CAPM ), которая используется для расчета ожидаемой доходности актива, ковариация между ценными бумагами и рынком используется в формуле для одной из ключевых переменных модели, бета . В CAPM бета измеряет волатильность или систематический риск ценной бумаги по сравнению с рынком в целом; это практическая мера, основанная на ковариации для оценки подверженности инвестора риску, характерному для одной ценной бумаги.
Между тем, теория портфелей использует ковариации для статистического снижения общего риска портфеля за счет защиты от волатильности за счет диверсификации с учетом ковариаций.
Краткая справка
Обладание финансовыми активами с доходностью, имеющей аналогичные ковариации, не обеспечивает большой диверсификации; следовательно, диверсифицированный портфель, вероятно, будет содержать набор финансовых активов с различными ковариациями.
Пример расчета ковариации
Предположим, что у аналитика компании есть набор данных за пять кварталов, который показывает квартальный рост валового внутреннего продукта ( ВВП ) в процентах (x) и рост новой линейки продуктов компании в процентах (y). Набор данных может выглядеть так:
- Q1: x = 2, y = 10
- Q2: x = 3, y = 14
- Q3: x = 2,7, y = 12
- Q4: x = 3,2, y = 15
- Q5: x = 4,1, y = 20
Среднее значение x равно 3, а среднее значение y равно 14,2. Чтобы вычислить ковариацию , сумма произведений значений x i минус среднее значение x, умноженное на значения y i минус средние значения y, будет разделена на (n-1) следующим образом:
Cov (x, y) = ((2 – 3) x (10 – 14,2) + (3 – 3) x (14 – 14,2) + … (4,1 – 3) x (20 – 14,2)) / 4 = (4,2 + 0 + 0,66 + 0,16 + 6,38) / 4 = 2,85
Рассчитав здесь положительную ковариацию, аналитик может сказать, что рост новой продуктовой линейки компании имеет положительную связь с квартальным ростом ВВП.
Источник
Степень взаимосвязи доходностей двух активов
При формировании портфеля степень взаимосвязи между доходностями двух активов можно определить с помощью показателей ковариации и корреляции.
Ковариация (covariance) – это статистическая мера взаимодействия двух случайных величин. Она говорит о степени зависимости двух переменных, например о зависимости доходностей двух ценных бумаг А и В.
Ковариация может принимать как положительные, так и отрицательные значения. При положительной ковариации доходностей двух бумаг с ростом доходности первой доходность второй будет расти. И наоборот, при падении доходности первой – доходность второй будет снижаться. При отрицательной ковариации рост доходности первой бумаги будет сопровождаться падением второй. Если ковариация равна нулю, то никакой зависимости не наблюдается либо она очень слаба. Чем больше значение ковариации, тем сильнее зависимость. Ковариация определяется по формуле:
| где | r(1,2)i. — доходность актива 1 или 2 в i-ом периоде, |
| E(ri1,2) — средняя (ожидаемая) доходность актива 1 или 2 за n периодов. |
Если необходимо рассчитать выборочную ковариацию, то приведенную формулу необходимо разделить на n периодов наблюдения (см. формулу выборочной дисперсии).
Ковариация зависит от единиц измерения величин, что ограничивает ее применение. Очень близкой к ковариации является другая статистическая мера – коэффициент корреляции (correlation coefficient). Он нормирует ковариацию для облегчения сравнения с другими парами независимых переменных. Ковариация двух случайных величин равна корреляции между ними, умноженной на произведение стандартных отклонений. Отсюда, коэффициент корреляции равен:
Коэффициент корреляции 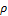
Пример: Портфель инвестора состоит из двух активов: А и В. Инвестор планирует три исхода событий в будущем, характеристики которых приведены в таблице. Определить коэффициент корреляции между двумя активами.
| Вероятность | Доходность актива А | Доходность актива В | |
| Исход 1 | 0,5 | 40% | — 20% |
| Исход 2 | 0,3 | ||
| Исход 3 | 0,2 | — 30% | 40% |
4. 
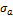
5. 
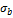
6. 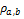
При расчете риска портфеля, состоящего из нескольких активов, необходимо учесть парные ковариации (корреляции) всех входящих в него активов.
Дисперсия портфеля на основе ковариации доходностей, например для трех активов входящих в портфель, определяется по формуле:
Каждый член двойной суммы включает в себя произведение весов двух ценных бумаг и их ковариацию.
Пример: Российский инвестор купил акции компании A на 600 тыс. долл., компании В на 400 тыс. долл. Стандартное отклонение доходности акции компании A в расчете на день составляет 1,4%, компании В – 1,55%. Курс доллара 1долл.=25 руб., стандартное отклонение валютного курса в расчете на один день 0,43%, коэффициент ковариации между курсом доллара и доходностью акции компании A равен 0,0903, доходностью компании В – 0,05332. Ковариация доходностей акции компании A и компании В равна 1,736. Определить стандартное отклонение доходности портфеля в расчете на день.
Решение: Риск инвестора обусловлен 3 факторами, которые необходимо учесть при расчете: падением курса доллара, а также возможным падением котировок акций компаний А и В. Валютный риск учитывается полностью, поэтому его удельный вес принимается равным единице.
1. 

2. 
3. 

Несложные алгебраические вычисления позволяют понять интерпретацию коэффициента корреляции:
§ при объединении в портфель активов с корреляцией +1 риск не уменьшается, а лишь усредняется;
§ идеальный портфель состоит из активов с корреляцией -1;
§ при отрицательной корреляции между активами риск портфеля меньше средневзвешенной суммы рисков, привносимых каждым конкретным активом, поэтому при формировании портфеля необходимо стремиться к объединению активов с наименьшей корреляцией доходностей. Этот частный случай диверсификации называется хеджированием.
Коэффициент бета
Относительное изменение доходности акции (портфеля акций) по сравнению с доходностью рынка, характеризуется коэффициентом бета – β. Этот коэффициент измеряет относительную неустойчивость доходности актива (портфеля) в сравнении с репрезентативным показателем доходности рынка в целом (например, каким-либо представительным индексом рынка или фьючерсом на него). Математический смысл коэффициента β следует из формулы оптимального (эффективного) портфеля:
| где | 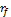 – ставка без риска; – ставка без риска; |
 – коэффициент бета актива; – коэффициент бета актива; | |
 – ожидаемая доходность по рынку за тот же период. – ожидаемая доходность по рынку за тот же период. |
Исходя из этой формулы, теория инвестиционного портфеля позволяет сделать вывод: премия за риск любого актива, включенного в оптимальный портфель, пропорциональна премии за риск, связанной с портфелем в целом. Коэффициентом пропорциональности выступает β.
Бета портфеля представляет собой средневзвешенную сумму значений бета активов, его составляющих:
Т.к. бета портфеля является средним значением беты ценных бумаг, входящих в портфель, то нет оснований предполагать, что увеличение диверсификации портфеля вызовет изменение беты портфеля, и, соответственно, рыночного риска портфеля в какую-либо сторону. Диверсификация портфеля позволяет усреднить рыночный риск.
Бета конкретного актива рассчитывается по формуле:
| где |  – корреляция между доходностью i-го актива и доходностью на рыночный индекс; – корреляция между доходностью i-го актива и доходностью на рыночный индекс; |
 – стандартное отклонение доходности на рыночный индекс; – стандартное отклонение доходности на рыночный индекс; | |
 – ковариация доходности i-го актива и доходности на рыночный индекс; – ковариация доходности i-го актива и доходности на рыночный индекс; | |
 – дисперсия доходности на рыночный индекс. – дисперсия доходности на рыночный индекс. |
Бета портфеля показывает, как рынок будет действовать на изменение доходности портфеля. Например, если бета портфеля равна 5, то увеличение доходности по рынку на 1% приведет к увеличению доходности портфеля на 5%. Такая же величина изменения риска, но в обратном направлении, приведет к снижению доходности портфеля на те же 5%.
Таким образом, активы с β > 1 более рискованны, чем с β
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Источник