Компания имеет возможность рекламировать свою продукцию

Новичок

Группа: Пользователи
Сообщений: 1
Регистрация: 29.2.2008
Город: Краснодар
Учебное заведение: Саратовский ВИРХБЗ

Доцент

Группа: Преподаватели
Сообщений: 3 614
Регистрация: 27.2.2007
Город: Екатеринбург
Вы: преподаватель

Пусть на радио отвoдится х1 минут, а на телевидение х2 минут в месяц. Тогда ограничения таковы:

15*x1+300*x2 =2*x2
x1 =0, x2>=0

Теперь о целевой функции. Примем эффективность одной минуты на радио за одну условную единицу эффективности — 1 у.е. (не представляю, в чем она измеряется). Тогда эффективность одной минуты на телевидении 25 у.е., а общая эффективность запланированной рекламы на радио и телевидение за месяц будет составлять z=1*x1+25*x2 у.е.

Источник

математика — Задача про рекламу

Фирма имеет возможность рекламировать свою продукцию, используя местные радио- и телевизионную сети. Затраты на рекламу в бюджете фирмы ограничены величиной $%1000$ $% в месяц. Каждая минута радиорекламы обходится в $%5$,$% а каждая минута телерекламы — в $%100$ $%. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения, но при этом фирма решила, что время радиорекламы не должно превышать двух часов. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в $%25$% раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определите оптимальное распределение финансовых средств, ежемесячно отпускаемых на рекламу, между радио- и телерекламой, если время можно покупать только поминутно.

задан 2 Июн ’15 13:33

serg55
8.4k ● 1 ● 47 ● 217
95&#037 принятых

2 ответа

Мне кажется, тут всё решается вручную, то есть симплекс-метода и всего прочего применять не надо.

Из неравенств $%x\ge2y$% и $%x+20y\le200$% следует, что $%22y\le200$%, откуда $%y\le9$% ввиду целочисленности. Тогда $%x+25y\le200+5y\le245$%. Максимум достигается при $%y=9$%, $%x=200-20y=20$%. Условия $%x/y\ge2$% и тем более $%x\le120$% при этом соблюдены.

отвечен 2 Июн ’15 15:54

falcao
262k ● 4 ● 37 ● 50

$%x,y$% — время радио- и телерекламы.

Тогда: $$ \begin Z=x+25y\to \max \\ 5x+100y\le 1000 \\ x \ge 2y \\ x\le 120 \\ x,y\in\mathbb_ <+>\end $$ Какой-нибудь метод ветвей и границ даст графическое решение .

Источник

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Читайте также: Свое дело отозвать чек

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Источник

Задачи на нахождение наибольшего/наименьшего значения величины (страница 2)

На двух заводах выпускают одинаковую продукцию. Известно, что если на первом заводе рабочие суммарно трудятся $t^2$ часов в день, то завод выпускает $t$ единиц продукции. Если на втором заводе рабочие суммарно трудятся $t^2$ часов в день, то завод выпускает $2t$ единиц продукции. Заработная плата на обоих заводах для одного рабочего составляет $300$ рублей в час. Определите, какое наибольшее количество товаров могут выпустить в день оба завода, если на зарплату в день рабочим выделяется $2\,166\,000$ рублей.

Пусть на первом заводе рабочие трудились $t^2$ часов, тогда завод выпустил $t$ единиц продукции; пусть на втором трудились $p^2$ часов, тогда завод выпустил $2p$ продукции. Следовательно, необходимо найти наибольшее значение величины $T=t+2p$ . Так как заработная плата в час составляет $300$ рублей, то $2\,166\,000=300(t^2+p^2)$ .
Выразим $t=T-2p$ и подставим в уравнение: \[2\,166\,000=300((T-2p)^2+p^2) \quad\Leftrightarrow\quad 5p^2-4Tp+T^2-7220=0\] Данное уравнение должно иметь корни, следовательно, его дискриминант должен быть неотрицательным: \[D=16T^2-4\cdot 5(T^2-7220)=4\cdot 5\cdot 7220-4T^2\geqslant 0\] Отсюда получаем, что $T^2\leqslant 5\cdot 7220=5^2\cdot2^2\cdot 19^2$ , следовательно, $T\in [0;190]$ (учитывая, что $T\geqslant 0$ , так как это количество продукции). Следовательно, наибольшее возможное $T$ – это $T=190$ .
Проверим, получаются ли при этом целые неотрицательные значения для $t$ и $2p$ (так как это количество продукции).
При $T=190$ дискриминант $D=0$ , следовательно, \[p=\dfrac<4\cdot 190><2\cdot 5>=76 \quad\Rightarrow \quad 2p=152 \quad\Rightarrow\quad t=190-152=38.\] Таким образом, проверка удалась и ответом является $T=190$ .

Фирма имеет возможность рекламировать свою продукцию, используя местных радио- и телевизионную сети. Затраты на рекламу в бюджете фирмы ограничены величиной $1000\$$ в месяц. Каждая минута радиорекламы обходится в $5\$$ , а каждая минута телерекламы – в $100\$$ . Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения, но при этом фирма решила, что время радиорекламы не должно превышать двух часов. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в $25$ раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определите оптимальное распределение финансовых средств, ежемесячно отпускаемых на рекламу, между радио- и телерекламой, если время можно покупать только поминутно.

(Задача от подписчиков)

Пусть фирма купила $y$ минут радиорекламы и $x$ минут телерекламы. Тогда из условия следует, что \[\begin 5y+100x\leqslant 1000\\ y\geqslant 2x\\ y\leqslant 120 \end\] Если обозначить за $1$ количество сбыта с одной минуты радиорекламы, то $F=25x+y$ – количество сбыта с $y$ минут радио- и $x$ минут телерекламы. Следовательно, нужно найти такие $x\geqslant 0$ и $y\geqslant 0$ , чтобы значение $F$ было наибольшим, причем $x$ и $y$ должны удовлетворять системе.
Изобразим область, которую задает данная система:

Область – четырехугольник $ABCD$ (с границей). Таким образом, нужно найти точку из данной области, в которой значение $F$ будет наибольшим.

Докажем, что эта точка будет находиться на отрезке $BC$ .
Заметим, что чем больше $x$ и $y$ , тем больше значение $F$ . Заметим также, что если взять любую точку, находящуюся внутри области, на $AD$ или на $AB$ , то при перемещении этой точки вправо (параллельно оси абсцисс) ее абсцисса будет увеличиваться, ордината оставаться прежней, следовательно, значение $F$ также будет увеличиваться. Таким образом мы дойдем до границы — ломаной $BCD$ .
Рассмотрим отрезок $CD$ . При движении точки по отрезку от $D$ к $C$ значение обеих координат точки будет увеличиваться, следовательно, значение $F$ будет увеличиваться, таким образом, среди всех точек отрезка $CD$ наибольшее значение $F$ будет принимать в точке $C$ .
Значит, наибольшее значение $F$ принимает в точке, находящейся на отрезке $BC$ .
Найдем абсциссы точек $B$ и $C$ . Для этого нужно найти абсциссы точек пересечения $y=200-20x$ с $y=120$ и $y=200-20x$ с $y=2x$ . Следовательно, абсцисса точки $B$ – это $x_b=4$ , абсцисса точки $C$ – это $x_c=\frac<100><11>$ . Значит, отрезок $BC$ задается уравнением $y=200-20x$ , $x\in \left[4;\frac<100><11>\right]$ .
Подставим: \[F=25x+200-20x=200+5x\] Данная функция принимает наибольшее значение при наибольшем значении $x$ . Вспомним, что $x$ к тому же должен быть целым неотрицательным. Так как $x\in \left[4;\frac<100><11>\right]$ , то наибольший такой $x_=9$ (так как $\frac<100><11>=9\frac1<11>$ ). Следовательно, \[y_=200-20\cdot 9=20.\]

9 минут телерекламы, 20 минут радиорекламы

Мебельная фирма производит книжные шкафы и серванты. На изготовление одного книжного шкафа расходуется $\frac13$ м $^2$ древесно-стружечной плиты, $\frac83$ м $^2$ сосновой доски и $\frac13$ человеко-часа рабочего времени.
Аналогичные данные для серванта даются числами: $\frac12$ м $^2$ древесно-стружечной плиты, $3$ м $^2$ сосновой доски и $1$ человеко-час.
Прибыль от реализации одного книжного шкафа составляет $6000$ рублей, от серванта – $16000$ рублей.
В течение одного месяца в распоряжении фирмы имеются $45$ м $^2$ древесно-стружечной плиты, $330$ м $^2$ сосновых досок и $80$ человеко-часов рабочего времени.
Какова максимальная ожидаемая месячная прибыль? Ответ дайте в млн. рублей.

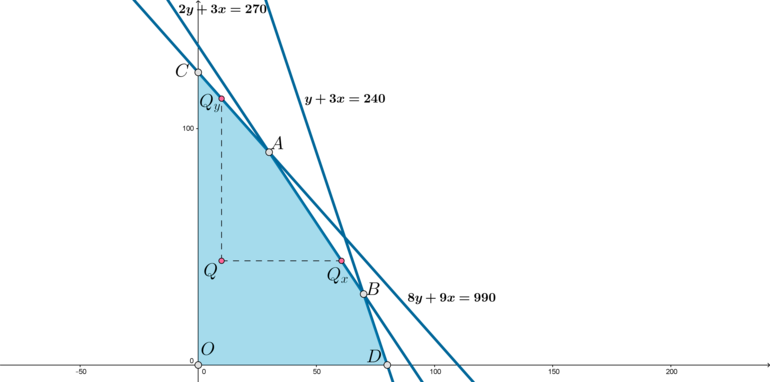
Пусть в течение месяца изготовили $y$ шкафов и $x$ сервантов. Тогда прибыль в тыс. рублей составит $P=6y+16x$ . Так как на изготовление шкафов и сервантов не может быть потрачено больше плит, досок и человеко-часов, чем имелось, то должно быть выполнено: \[\begin y\cdot \dfrac13+x\cdot \dfrac12\leqslant 45\\[2ex] y\cdot \dfrac83+x\cdot 3\leqslant 330\\[2ex] y\cdot \dfrac13+x\leqslant 80 \end \quad\Leftrightarrow\quad \begin 2y+3x\leqslant 270\\ 8y+9x\leqslant 990\\ y+3x\leqslant 240 \end\] Следовательно, при выполнении этих условий (системы) необходимо найти наибольшее значение для $P$ .

Графиком данной системы является область с границей, изображенная на рисунке (учитывая, что $x,y\geqslant 0$ , так как это количество изделий):

Причем сразу заметим, что $x,y$ также должны принимать только целые значения.
Таким образом, необходимо найти такую точку из данной области, в которой значение функции $P(x,y)=6y+16x$ будет наибольшим.

1) Докажем сначала, что наибольшее значение функция $P$ будет принимать точно на границе $CABD$ области.
Действительно, возьмем точку $Q(x;y)$ внутри области (или на $CO, OD$ ). Заметим, что при увеличении $x$ или $y$ значение функции $P$ будет увеличиваться.
Так как $Q$ находится внутри области, то все точки, находящиеся на отрезках $QQ_x$ и $QQ_y$ ( $QQ_x\parallel Ox$ , $QQ_y\parallel Oy$ ), а также между этими отрезками и границей области, будут иметь большие координаты по $x$ или по $y$ , чем $Q$ . Следовательно, в них значение функции $P(x,y)$ будет больше, чем в точке $Q$ . Таким образом, для любой точки внутри области найдется всегда точка на границе, в которой значение функции $P$ будет больше.
Следовательно, будем искать точку, в которой значение $P$ максимально, на границе $CABD$ .

2) Заметим, что эта граница области разбивается на отрезки: $CA, AB, BD$ .
Найдем координаты точек $A, B, C, D$ : $A(30;90)$ , $B(70;30)$ , $C\left(0;\frac<495>4\right)$ , $D(80;0)$ .
Рассмотрим каждый из отрезков по отдельности.

Отрезок $CA$ .
Это часть прямой $8y+9x=990$ при $y\in \left[90;\frac<495>4\right]$ . Выразим $x=110-\frac89y$ и подставим в $P$ : \[P=1760-\dfrac<74>9y\leqslant 1760-\dfrac<74>9\cdot 90=1020.\] Следовательно, наибольшее значение $P$ – это $1020$ тыс. рублей.

Отрезок $AB$ .
Это часть прямой $2y+3x=270$ при $y\in \left[30;90\right]$ . Выразим $x=90-\frac23y$ и подставим в $P$ : \[P=1440-\dfrac<14>3y\leqslant 1440-\dfrac<14>3\cdot 30=1300.\] Следовательно, наибольшее значение $P$ – это $1300$ тыс. рублей.

Отрезок $BD$ .
Это часть прямой $y+3x=240$ при $x\in \left[70;80\right]$ . Выразим $y=240-3x$ и подставим в $P$ : \[P=1440-2x\leqslant 1440-2\cdot 70=1300.\] Следовательно, наибольшее значение $P$ – это $1300$ тыс. рублей.

Таким образом, наибольшее значение $P$ достигается на отрезках $AB$ и $BD$ , а именно в точке с координатами $x=70$ и $y=30$ .
Следовательно, в млн. рублей наибольшая прибыль равна 1,3.

Источник