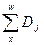Коммутационные числа при норме доходности 5

Для удобства и стандартизации расчетов нетто-ставок в личном страховании используются коммутационные числа Dx, Nx, Сх, Мх, Rx. В общем виде их расчет может быть осуществлен по известным формулам [c.405]

Знак п означает предельный возраст в таблице смертности. Коммутационные числа для нормы доходности 5% и возраста 10 лет будут иметь следующие значения [c.405]

Рассчитаем единовременную нетто-ставку на дожитие, используя коммутационные числа. [c.406]

На 1 руб. страховой суммы единовременная нетто-ставка в коммутационных числах может быть рассчитана по следующей формуле [c.406]

Рассчитаем единовременную тарифную ставку на случай смерти с помощью коммутационного числа Мх. [c.410]

Используя данные задачи 10.6, произведите расчет единовременной нетто-ставки, опираясь на коммутационные числа. [c.433]

Используя коммутационные числа (см. приложение 13), рассчитайте размер единовременной нетто-ставки на случай смерти, если клиент в возрасте 51 года заключил договор страхования на 4 года. Норма доходности 5%. [c.433]

Для сокращения записей и трудоемкости расчетов применяют так называемые коммутационные числа. Одним из элементов подсчета коммутационных чисел является дисконтный коэффициент для выбранной ставки процента. В приложениях к настоящей главе представлены таблицы коммутационных чисел, рассчитанных по ставке 9% годовых. Для пенсионных расчетов из этих таблиц применяют только два показателя — числа Dx, Nx [c.304]

КОММУТАЦИОННЫЕ ЧИСЛА —КОНВЕРСИЯ ЗАЙМОВ [c.544]

КОММУТАЦИОННЫЕ ЧИСЛА — вспомогательные величины, применяемые для упрощения математич. формул и облегчения расчетов при построении финансовых основ (тарифов, резерва взносов и др.) различных видов страхования жизни. Размер К. ч. зависит от соответствующих показателей, содержащихся в таблице смертности (см.), принятой для построения тарифов по страхованию жизни, а также от нормы доходности. [c.544]

Задача 9.24. Рассчитайте единовременную нетто-ставку на 100 руб. страховой суммы по страхованию гражданина на случай смерти через 5 лет, используя коммутационные числа. [c.41]

Данные для расчета. Возраст страхователя — 41 год. Срок страхования — 5 лет. Коммутационные числа M4i = 10992 М45 = 10502 Д41 = 27341. [c.41]

Данные для расчета. Возраст страхователя 41 год. Коммутационные числа M4i = 10992 Д41 = 27341. [c.41]

Задача 9.26. Рассчитайте единовременную нетто-ставку на 100 руб. страховой суммы на дожитие, используя коммутационные числа. [c.41]

Данные для расчета Возраст страхователя — 41 год. Срок страхования — 10 лет. Коммутационные числа Д41 = = 27341 Д50 = 19859. [c.41]

Между коммутационными числами обеих групп существуют определенные взаимозависимости [c.340]

Источник

4.3. Коммутационные числа

Таблица смертности позволяет установить вероятное число выплат по договорам страхования, а при известных страховых суммах – размер страхового фонда, которым должна располагать страховая компания, чтобы выплатить страховые суммы.

Однако прежде чем установить долю участия каждого из страхователей в создании страхового фонда, необходимо учесть еще один показатель – норму доходности.

Дело в том, что временно свободные средства, аккумулированные страховой компанией, инвестируются. За пользование ими уплачивается сумма процентов, определяемая процентной ставкой (нормой доходности) i . Эта сумма заранее уменьшает (дисконтирует) подлежащие уплате взносы страхователей. Для проведения таких расчетов используются методы теории процентных ставок, использующие понятие дисконтирующего множителя. В страховании жизни обычно используется дисконтирующий множитель, определяемый постоянной процентной ставкой по формуле

V(i) = (4.3)

Однако в условиях инфляции и, следовательно, изменчивости и слабой предсказуемости процентных ставок при расчете долгосрочного страхования появляются проблемы. Так, если взять для расчетов высокую норму доходности i, то это может понизить финансовую устойчивость страховой компании, так как доходы будут ниже планируемых ввиду падения величины i. При занижении i долгосрочное страхование теряет привлекательность для населения.

Методики исчисления тарифных ставок, применяемые в настоящем пособии, позволяют учесть изменчивость процентной ставки с помощью введения непрерывных процентов, в частности силы процента.

Показатели, необходимые для исчисления тарифных ставок, имеются в таблицах смертности и дисконтирующих множителей.

Nx = Dx + …+ Dw , (4.5)

Cx = dx · Vx+1 , (4.6)

Mx = Cx + … + Cw , (4.7)

Rx = Mx + … + Mw . (4.8)

Здесь и далее w – предельный возраст таблицы смертности. Как будет показано в последующих разделах, тарифные ставки для различных видов страхования выражаются через коммутационные числа (4.4) – (4.8) в достаточно простом виде. Это обстоятельство позволяет резко упростить расчеты, если имеются таблицы коммутационных чисел. Для каждой таблицы смертности можно составить серию таблиц коммутационных чисел, каждая из которых соответствует своей процентной ставке i. Имеются сборники коммутационных чисел для наиболее употребительных значений параметра i. В табл.4.2 представлены коммутационные числа, вычисленные на основании табл.4.1 смертности, при норме доходности i= 0,03.

Источник

Коммутационные функции

Для сокращения записи страховых аннуитетов и упрощения расчетов применяют так называемые коммутационные функции или коммутационные числа. Смысл этих чисел трудно, хотя и возможно, содержательно интерпретировать. Их проще воспринимать как чисто технические, вспомогательные средства.

Стандартные коммутационные функции делятся на две группы. В основу первых положены числа доживающих до определенного возраста, вторых – числа умерших. Основными в первой группе являются функции D_x и N_x:

D_x=l_xv x , N_x=

где v – дисконтный множитель по сложной ставке i , w — предельный возраст, учитываемый в таблице смертности.

В некоторых актуарных расчетах необходимы суммы коммутационных чисел D_x для заданных возрастных интервалов. В этих случаях можно воспользоваться коммутационными числами N_x:

D_x₊_t=N_n₊₁ – N_x₊_k₊₁

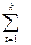
На практике применяются еще два варианта функции N_x, к которым обращаются тогда, когда платежи производятся m раз в году. Так, для платежей постнумерандо с достаточной для практических расчетов точностью применим следующее выражение:

Для платежей пренумерандо

Наиболее важными коммутационными функциями второй группы являются C_x

и M_x: C_x=d_xv x +1 , M_x= 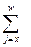C_j

Между коммутационными числами обеих групп существуют определенные взаимозависимости:

Аналогично можно доказать, что

Страховые организации разрабатывают таблицы коммуникационных функции с учетом принятых в них норм доходности.

Таблица 4.2 Фрагмент таблицы коммутационных чисел

x	l_x	D_x	N_x	N_x (12)	C_x	M_x
100 000	21 199	244 593	245 309	28,98	1003,6
99 851	19 420	223 393	232 294	30,82	974,7
99 678	17 786	203 973	212 125	31,98	943,8
…
96 991	80 677	84 027	25,55	648,9
…
94 951	49 910	52 042	20,78	530,3
…
92 327	30 376	31 723	19,09	431,4
…
83 640	10 465	10 981	14,54	206,7
…
68 505	10,25	134,7
…
45 654	5,72	53,1
…
19 760	2,14	13,0

При страховании супружеских пар возникает необходимость в коммутационной функции:

Величина l_xy определена при расчете _nP_xy

Функцию D_xy=l_xy*v ( x + y )/2 можно получить на основе коммутационной функции D_x, D_y следующим образом:

Поскольку произведение коммутационных чисел имеют большую размерность, то их обычно умножают на 10 -3 .

Пример: определим коммутационные числа D_50;45 и D_55;50 для супружеской пары возраст супругов 50 и 45 лет. Находим:

Коммутационные числа при условии, что процентная ставка равна 9%, имеют следующие значения (первая строка – для мужчины, вторая – для женщины):

D_50;45=10 -3 *1124,8*1991,9*1,09 47,5 =134 308;

D_55,50=10 -3 *673,1*1268,8*1,09 5+47,5 =78 770.

По аналогии с функцией N_x найдем: N_xy= 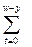D_x₊_t_; _y₊_t.

Тестовые задания

4011324. Аннуитет – это:

1. Период времени между двумя последовательными платежами;

2. Последовательность периодических платежей, сделанных через различные промежутки времени;

3. Последовательность периодических платежей, сделанных через одинаковые промежутки времени;

4 Одноразовый платёж.

4023142. Срок аннуитета – это:

1. Время от начала первого интервала платежа до начала последнего интервала платежа;

2. Время от начала первого интервала платежа до окончания последнего интервала платежа;

3. Время от окончания первого интервала платежа до начала последнего интервала платежа;

4. Нет правильного ответа.

4032314. Аннуитет называется обыкновенным, если:

1. Срок платежа осуществляется в моменты окончания интервалов платежа;

2. Срок платежа осуществляется в начальный момент интервала платежа;

3. Интервал платежа совпадает с периодом начисления процента;

4. Срок не имеет значения, все зависит от суммы платежа.

4041234. Настоящая стоимость обыкновенного аннуитета определяется как:

1. Датированная сумма эквивалентная всей серии платежей независимо от срока аннуитета;

2. Датированная сумма эквивалентная всей серии платежей на начало срока аннуитета;

3. Сумма всех платежей;

4. Сумма всех платежей без учета срока платежей.

4052314. Итоговая сумма обыкновенного аннуитета определяется как:

1. Датированная сумма эквивалентная всей серии платежей на начало срока;

2. Датированная сумма эквивалентная всей серии платежей на конец срока;

3. Сумма всех платежей;

4. Сумма всех платежей без учета срока платежей.

4063142. Аннуитет называется простым, если:

1. Срок платежа осуществляется в момент, обусловленный договором;

2. Интервал платежа совпадает с периодом начисления процента;

3. Срок платежа осуществляется в момент окончания интервала платежа;

4. Периодический платеж производится в начальный момент времени.

4073142. Аннуитет называется страховым, если:

1. Выплата ренты не зависит от наступления страхового события, а зависит лишь от времени уплаченной страховой суммы;

2. Выплата ренты зависит от наступления страхового события;

3. Выплата ренты не зависит от наступления страхового события при условии, что страхователь назвал наследника;

4. Нет правильного ответа.

4082413. Полагающий аннуитет – это:

1. Когда периодические платежи производятся в начальные моменты интервалов платежа, со сроком, начинающимся датой первого и заканчивающимся через один интервал после последнего платежа;

2. Когда периодические платежи производятся в конечные моменты интервала и заканчиваются за один интервал до даты погашения;

3. Когда интервал платежа совпадает с периодом начисления процента;

4. Нет правильного ответа.

4092143. Факторами определяющими стоимость страхового аннуитета являются: а) демографический, отражаемый в таблице смертности; б) процентная ставка (установленная норма доходности); в) длительность отсрочки выплат; г) срок аннуитета.

4101324. Аннуитет называется отсроченным, если:

1. Срок аннуитета не изменяется;

2. Срок аннуитета устанавливается с даты заключения сделки;

3. Срок аннуитета устанавливается с даты в будущем относительно даты заключения сделки;

4. Интервал платежа совпадает с периодом начисления процента.

4111234. Чем выше показатель смертности:

1. Тем выше страховая (актуарная) стоимость аннуитета;

2. Тем ниже страховая (актуарная) стоимость аннуитета;

3. Страховая (актуарная) стоимость аннуитета не меньше;

Источник

Практикум 4. Личное страхование

Расчет тарифных ставок по страхованию жизни

Расчет тарифных ставок по страхованию жизни имеет определенные особенности. Размер ставки зависит как от возраста застрахованного, так и от срока страхования, а также, от некоторых других факторов. В основу расчета тарифных ставок по страхованию жизни положены так называемые таблицы смертности.

В предложенных задачах для расчетов используются таблицы смертности (см. Приложение 1) и построенные на их основе таблицы коммутационных чисел (см. Приложение 2).

Задача 1. Для лица в возрасте 42 лет рассчитайте:

Вероятность прожить еще один год;
Вероятность умереть в течение предстоящего года жизни;
Вероятность прожить еще три года;
Вероятность умереть в течение предстоящих трех лет;
Вероятность умереть на четвертом году жизни (в возрасте 46 лет).

Задача 2. Для лица в возрасте 43 лет рассчитайте:

Вероятность прожить еще один год;
Вероятность умереть в течение предстоящего года жизни;
Вероятность прожить еще три года;
Вероятность умереть в течение предстоящих трех лет;
Вероятность умереть на четвертом году жизни (в возрасте 47 лет).

Задача 3. Рассчитайте для лица в возрасте 46 лет:

Вероятность прожить еще один год;
Вероятность умереть в течение предстоящего года жизни;
Вероятность прожить еще три года;
Вероятность умереть в течение предстоящих трех лет;

Методические рекомендации по решению задач 1 – 3

вероятность смерти (g_x) при переходе от возраста х,к возрасту (х+1) лет:

где d_x – число умирающих при переходе от возраста х к возрасту (х+1) лет;

вероятность дожития (р_х) лица в возрасте хлет до возраста (х+1) лет;

Пример. Для лица в возрасте 45 лет рассчитайте:

Вероятность прожить еще один год.
Вероятность умереть в течение предстоящего года жизни.
Вероятность прожить еще два года.
Вероятность умереть в течение предстоящих двух лет.
Вероятность умереть на третьем году жизни в возрасте 48 лет.

Решение.

Определяем для лица в возрасте 45 лет:

Вероятность умереть в течение предстоящего года жизни

Вероятность прожить еще два года

Вероятность умереть в течение предстоящих двух лет

Вероятность умереть на третьем году жизни в возрасте 48 лет

Задача 4. Рассчитайте единовременную брутто-премию для страхователя в возрасте 45 лет, застрахованного по смешанному страхованию жизни сроком на три года. Норма доходности – 8 %. Страховая сумма – 25 тыс. руб. Доля нагрузки в брутто-ставке – 10 %. (данные для решения задачи см. в Приложении 1).

Задача 5. Страхователь в возрасте 44 лет заключил договор страхования на случай смерти сроком на пять лет (норма доходности – 8 %, страховая сумма – 20 тыс. руб., доля нагрузки – 9 %).

Определите через коммутационные числа (см. Приложение 2):

единовременную нетто-ставку, брутто ставку и брутто-премию;
годовую нетто-ставку, брутто-ставку и брутто-премию.

Что выгоднее для страхователя: платить взносы по частям ежегодно или единовременно?

Задача 6. Рассчитайте единовременную брутто-премию для страхователя в возрасте 45 лет, застрахованного по смешанному страхованию жизни сроком на три года с использованием коммутационных чисел. Норма доходности – 8%. Страховая сумма – 25 тыс. руб. Доля нагрузки в брутто-ставке – 10% (данные для решения задачи см. в Приложении 2).

Задача 7. Рассчитайте единовременную нетто-ставку на 100 руб. страховой суммы по страхованию гражданина на случай смерти через 5лет, используя коммутационные числа. Известно, что возраст страхователя 41 год, срок страхования 5 лет. Коммутационные числа: М₄₁=10992; М₄₅= 10502; D₄₁=27341.

Задача 8. Страхователь в возрасте 42 лет заключил договор страхования на случай смерти сроком на два года (норма доходности – 8%.)

Единовременную нетто-ставку на случай смерти двумя способами:
- используя данные таблицы смертности;
- используя коммутационные числа.
Годовую нетто-ставку.
Брутто-ставку (единовременную и годовую), если нагрузка составляет 11 %.
Брутто-премию (единовременную и годовую), если страховая сумма – 30 тыс. руб.

Задача 9. Для страхователя в возрасте 41 года, заключившего договор страхования жизни сроком на два года (норма доходности – 8 %, страховая сумма – 15 тыс. руб.) рассчитайте:

Размер единовременной нетто-ставки на дожитие и на случай смерти рассчитайте двумя способами:
- используя данные таблицы смертности;
- через коммутационные числа;
Размер единовременной брутто-ставки при смешанном страховании жизни (в рублях на 100 руб. страховой суммы), если доля нагрузки в брутто-ставке – 11 %;
Единовременную брутто-премию при смешанном страховании жизни.

Методические рекомендации по решению задач 4–9

Единовременная ставка по страхованию на дожитие для лица в возрасте х лет при сроке страхования т лет в расчете на 100 руб. страховой суммы (_nE_x) определяется:

где l_x+n – число лиц, доживающих до возраста x + n (берется из таблицы смертности);

l_x – число лиц, подлежащих страхованию (достигших возраста х лет из 100000 родившихся);

V n – дисконтный множитель, который определяется по формуле:

где i – норма доходности инвестиций;

n – срок страхования.

Единовременная нетто-ставка (_nA_z) на случай смерти на определенный срок вычисляется:

где – число лиц, умирающих при переходе от х лет к возрасту (х+1) по годам за срок страхования.

При смешанном страховании на дожитие и на случай смерти рассчитывается совокупная нетто-ставка:

Брутто-ставка определяется по формуле:

где f – доля нагрузки в брутто-ставке (%).

Пример. Рассчитайте единовременную брутто-премию для страхователя в возрасте 45 лет, застрахованного по смешанному страхованию жизни сроком на три года. Норма доходности – 8 %. Страховая сумма – 25 тыс. руб. Доля нагрузки в брутто-ставке – 10 %.

Решение.

1. Единовременные нетто-ставки для лица в возрасте 45 лет сроком на 3 года:

со 100 руб. страховой суммы.

1.2. На случай смерти:

3,22 руб. со 100 руб. страховой суммы.

1.3. При смешанном страховании жизни:

2. Единовременную брутто-ставку при смешанном страховании жизни:

88,5 руб. со 100 руб. страховой суммы.

3. Единовременную брутто-премию:

Для упрощения расчетов тарифных ставок по страхованию жизни применяются специальные показатели – коммутационные числа.

Страховые выплаты для возраста Х:

Фонд страховых взносов:

Выплаты для совокупности страхователей:

Фонд страхового запаса:

V – дисконтирующий множитель;

l – число лиц, доживающих до возраста Х лет;

n – процентная ставка капитала в долях единицы;

ω – предельный возраст по таблице смертности.

В результате преобразований формулы расчета нетто-ставок через коммутационные числа примут вид:

Для расчета единовременной нетто-ставки для пожизненного страхования на случай смерти применяется формула:

Единовременная нетто-ставка на дожитие рассчитывается по формуле:

Годовая нетто-ставка (взнос уплачивается в начале страхового года) для лица в возрасте х лет на дожитие при сроке страхования n лет:

Годовая нетто-ставка (взнос уплачивается в начале страхового года) для лица в возрасте х лет на случай смерти при страховании на определенный срок:

Годовая нетто ставка (взнос уплачивается в начале страхового года) для лица в возрасте х лет на случай смерти при пожизненном страховании:

Пример. По данным предыдущего примера рассчитать нетто-ставки по вышеуказанным формулам через коммутационные числа, используя таблицы.

Решение.

1. Единовременную нетто-ставку для лица в возрасте 45 лет при сроке страхования три года:

1.2. На случай смерти:

2. Единовременную нетто-ставку на случай смерти для лица в возрасте 45 лет при пожизненном страховании:

3. Годовую нетто-ставку (взнос уплачивается в начале страхового года):

3.1. На дожитие для лица в возрасте 45 лет при сроке страхования три года:

3.2. При страховании на случай смерти для лица в возрасте 45 лет на 3 года:

3.3. При пожизненном страховании на случай смерти:

Вопросы для самостоятельного рассмотрения

Определите основные особенности расчета тарифных ставок по страхованию жизни.
Назовите базовые типы договоров страхования жизни.
Дайте определение формам и видам страхования от несчастных случаев в РФ.
Определите особенности установления размера страховых выплат по добровольному страхованию от несчастных случаев в зависимости от степени потери трудоспособности в результате несчастного случая.
Определите особенности организации обязательного медицинского страхования (ОМС) в РФ.
В чем состоят особенности организации добровольного медицинского страхования (ДМС) в РФ?

Приложение 1

Выписка из таблицы смертности

Возраст в годах (x)

Число доживающих до возраста х лет (l_x)

Число умирающих при переходе от возраста х к возрасту х+1 лет (d_x)

Вероятность умереть в течение предстоящего года жизни (q_x)

Вероятность дожить до возраста х+1 лет (p_x)

Источник