- Задача №48. Расчёт показателей вариации
- Решение:
- CFA — Коэффициент вариации
- Формула коэффициента вариации.
- Пример расчета коэффициента вариации для ставок доходности.
- Коэффициент вариации | Coefficient of Variation, CV
- Формула
- Интерпретация
- Пример расчета
- Расчет коэффициента вариации
- Понятие коэффициента вариации
- Формула расчета коэффициента вариации
- Пример расчета коэффициента вариации
- Онлайн калькулятор расчета коэффициента вариации
Задача №48. Расчёт показателей вариации
У инвестора имеется две альтернативы вложения денежных средств в деятельность торговых компаний А и В. Анализ показал, что рентабельность аналогичных компаний за последние 5 лет составила:
| Организации | 1 год | 2 год | 3 год | 4 год | 5 год |
|---|---|---|---|---|---|
| Компания А (Рентабельность продаж,%) | 21 | 14 | 30 | 29 | 12 |
| Компания В (Рентабельность продаж,%) | 17 | 24 | 25 | 28 | 15 |
Исходя из критерия риска, выберите и обоснуйте наиболее предпочтительный для инвестора вариант (рассчитайте среднее квадратическое отклонение и коэффициент вариации).
Решение:
Рассчитаем среднее значение рентабельности продаж по формуле средней арифметической простой:
Построим вспомогательную таблицу расчётных данных:
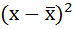
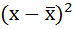
Средняя рентабельность продаж для организации А:
Средняя рентабельность продаж для организации В:
Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в дискретных рядах распределения производится по формуле:
Среднее квадратическое отклонение определим по формуле:
Коэффициент вариации рассчитывается по формуле:
По величине коэффициента вариации можно судить о степени вариации рентабельности продаж. Чем больше его величина, тем больше разброс значения признаков вокруг средней, тем более рискован проект.
Вложения денежных средств в деятельность торговой компании А подвержены большему риску, так как коэффициент вариации больше и он очень высокий. Поэтому для вложения денежных средств наиболее предпочтителен вариант инвестирования в деятельность торговой компании В.
Источник
CFA — Коэффициент вариации
Коэффициент вариации – относительная мера дисперсии и поэтому он полезен для сравнения изменчивости финансовых данных, выраженных в разных единицах измерения. Рассмотрим коэффициент вариации в рамках изучения количественных методов по программе CFA.
Ранее мы отмечали, что стандартное отклонение легче интерпретировать, чем дисперсию, поскольку стандартное отклонение выражается в тех же единицах измерения, что и наблюдения.
Иногда нам может быть трудно понять, что означает стандартное отклонение с точки зрения относительной степени изменчивости различных наборов данных, либо потому, что наборы данных имеют значительно отличающиеся средние, либо потому, что наборы данных имеют разные единицы измерения.
Далее мы рассмотрим относительную меру дисперсии — коэффициент вариации, который может быть полезен в таких ситуациях. Относительная дисперсия (англ. ‘relative dispersion’) — это значение дисперсии, рассчитанное относительно контрольного значения.
Мы можем проиллюстрировать проблему интерпретации стандартного отклонения для двух значительно отличающихся наборов данных, используя две гипотетические выборки финансовых данных.
Первая выборка включает небольшие компании с объемом продаж за 2003 год в размере €50 млн., €75 млн., €65 млн. и €90 млн.
Вторая выборка включает крупные компании с объемом продаж за 2003 году в размере €800 млн., €825 млн., €815 млн. и €840 млн.
Используя Формулу 14, мы можем убедиться, что стандартное отклонение продаж для обоих выборок составляет €16.8 млн.
Вторая выборка была создана путем добавления €750 млн. к каждому наблюдению из первой выборки. Стандартное отклонение (и дисперсия) имеет свойство оставаться неизменным, если мы добавляем постоянную величину к каждому наблюдению.
В первой выборке самое большое наблюдение, €90 млн., — на 80% больше, чем самое маленькое наблюдение, €50 млн. Во второй выборке самое большое наблюдение всего на 5% больше, чем самое маленькое наблюдение.
По сути, стандартное отклонение в размере €16.8 млн. представляет собой высокую степень изменчивости для первой выборки со средними продажами в размере €70 млн., но незначительную степень изменчивости для второй выборки, средние продажи которой составляют €820 млн.
Коэффициент вариации полезен в ситуациях, подобных только что описанной.
Формула коэффициента вариации.
Коэффициент вариации или CV (от англ. ‘coefficient of variation’), представляет собой отношение стандартного отклонения набора наблюдений к их среднему значению:
где s — стандартное отклонение выборки, а \(\overline X \) — среднее значение выборки.
(на практике CV обычно рассчитывается в процентах, как \(100( s / \ \overline X) \) ).
Например, когда наблюдения представляют собой ставки доходности, коэффициент вариации измеряет величину риска (стандартное отклонение) на единицу средней доходности. Выражая величину вариации относительно среднего значения наблюдений, коэффициент вариации позволяет напрямую сравнивать дисперсию для различных наборов данных.
Коэффициент вариации не привязан к шкале измерения (то есть он не имеет единиц измерения).
Мы можем проиллюстрировать применение коэффициента вариации на нашем предыдущем примере двух выборок финансовых данных компаний.
- Коэффициент вариации для первой выборки составляет (€16.8 млн.) / (€70 млн.) = 0,24.
- Коэффициент вариации для второй выборки составляет (€16.8 млн.) / (€820 млн.) = 0,02.
Это подтверждает нашу интуитивную догадку о том, что первая выборка имеет гораздо большую изменчивость продаж, чем вторая выборка.
Обратите внимание, что 0,24 и 0,02 являются «чистыми числами» в том смысле, что они не содержат единиц измерения (поскольку мы разделили стандартное отклонение на среднее значение, которое измеряется в тех же единицах, что и стандартное отклонение).
Если нам нужно сравнить дисперсию наборов данных, выраженных в разных единицах измерения, коэффициент вариации может быть весьма полезен, поскольку он не привязан к единицам измерения.
Приведенный ниже пример иллюстрирует расчет коэффициента вариации.
Пример расчета коэффициента вариации для ставок доходности.
Таблица 24 включает среднегодовую доходность и стандартные отклонения, рассчитанные на основе месячной доходности основных фондовых индексов четырех азиатско-тихоокеанских рынков. Это индексы S&P/ASX 200 Index (Австралия), Hang Seng Index (Гонконг), Straits Times Index (Сингапур) и KOSPI Composite Index (Южная Корея).
| № предложения цены | Значение цены, руб., х | (xi — хсреднее) 2 |
|---|---|---|
| 1 | 17,74 | 3,8 |
| 2 | 13,69 | 4,41 |
| 3 | 16 | 0,04 |
| 4 | 11,87 | 15,37 |
| 5 | 11,21 | 20,98 |
| 6 | 15,09 | 0,49 |
| 7 | 19,49 | 13,69 |
| 8 | 19,97 | 17,47 |
| 9 | 17,03 | 1,54 |
| Итого | 142,09 | 77,79 |
Для вычисления используем следующую формулу:
Определим средне значение: хсреднее = (17,74 + 13,69 + 16 + 11,87 + 11,21 + 15,09 + 19,49 + 19,97 + 17,03) / 9 = 15,79 руб.
Среднее квадратическое отклонение: σ = √(77,79 / 9) = 2,94.
Коэффициент вариации: ν = 2,94 / 15,79 * 100 = 18,62%.
Интерпретация. Полученное значение исследуемого показателя показывает, что колеблемость цены относительно небольшая и составляет 18,62% среднего уровня. Полученное значение также указывает на однородность исследуемой совокупности, т.к. полученное значение коэффициента вариации менее 33%.
Внимание! Расчет коэффициента вариации по 44 ФЗ имеет свои особенности, поэтому приводим отдельный пример расчета коэффициента вариации по 44 ФЗ
Онлайн калькулятор расчета коэффициента вариации
В заключении приводим небольшой онлайн калькулятор расчета коэффициента вариации онлайн, используя который, Вы можете самостоятельно выполнить расчет указанного показателя онлайн. При заполнении формы калькулятора расчета коэффициента вариации онлайн внимательно соблюдайте размерность полей, что позволит выполнить вычисления онлайн быстро и точно. Дробные величины должны вводиться с точкой, а не с запятой! В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает онлайн калькулятор расчета коэффициента вариации. Для расчета данного показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет». Обратите внимание, что расчет коэффициента вариации онлайн калькулятором осуществляется только по несгруппированным данным.
Онлайн-калькулятор расчета коэффициента вариации:
Источник
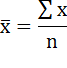
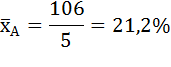
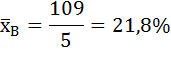
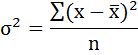
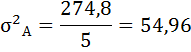
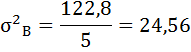
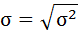
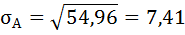
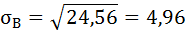
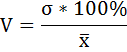
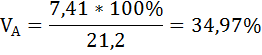
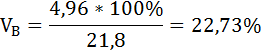

 — ожидаемое (среднее) значение случайной величины.
— ожидаемое (среднее) значение случайной величины.
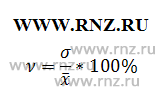 Формула расчета коэффициента вариации
Формула расчета коэффициента вариации Формула расчета точного значения коэффициента вариации
Формула расчета точного значения коэффициента вариации