Коэффициент корреляции доходностей активов формула

Корреляция в инвестициях на форексе и бирже

Валюты и биржевые активы не могут существовать в вакууме. Они связаны между собой многочисленными причинно-следственными связями. Поэтому изменение цены одного инструмента неизбежно влечёт за собой цепочку других изменений. Но если, например, фьючерсы на какао не вызовут паники на рынке нефти, то резкое укрепление доллара отразится на всех рынках (например, приведет к девальвации рубля). Зависимость между изменениями двух и более величин принято называть корреляцией. Сегодня я рассмотрю это явление с точки зрения инвестиций.

Что это такое корреляция: формулы и зависимости

Я веду этот блог уже более 6 лет. Все это время я регулярно публикую отчеты о результатах моих инвестиций. Сейчас публичный инвестпортфель составляет более 1 000 000 рублей.

Специально для читателей я разработал Курс ленивого инвестора, в котором пошагово показал, как наладить порядок в личных финансах и эффективно инвестировать свои сбережения в десятки активов. Рекомендую каждому читателю пройти, как минимум, первую неделю обучения (это бесплатно).

Корреляцией между двумя величинами называется статистическая взаимосвязь, при которой изменение одной из величин приводит к систематическому изменению другой. Количественной мерой корреляции является линейный коэффициент корреляции (называемый также коэффициентом корреляции Пирсона) , вычисляемый по формуле:

• r_xy – коэффициент корреляции значений величин x и y;
• d_x – отклонение некоторого значения ряда x от среднего значения этого ряда;
• d_y – отклонение некоторого значения ряда y от среднего значения этого ряда.

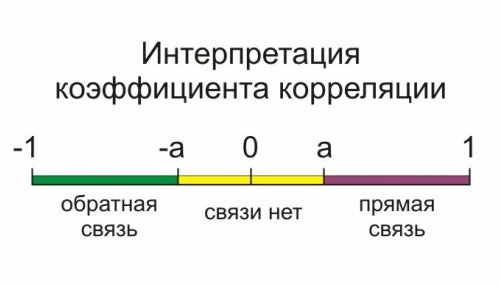
Диапазон возможных значений коэффициента корреляции находится между +1 и -1. При этом возможны следующие варианты:

• +1 – прямая зависимость между величинами;
• |r_xy| > 0.7 – ярко выраженная зависимость между величинами;
• 0.4 0.7 – средне выраженная зависимость между величинами;
• |r_xy|

Источник

Корреляция активов на финансовых рынках

Что такое корреляция?

Начнем с такого примера. Вы наполняете свой инвестиционный портфель различными инструментами (акциями, облигациями, чем-то еще), но неожиданно замечаете, что в процессе инвестирования все результаты движутся преимущественно в одну сторону. Т.е. вы получаете либо заметную доходность, либо существенный убыток.

Если первая ситуация нас радует, то вторая сильно печалит и мы начинаем задумываться, все ли сделали правильно. И хотя убытки, даже порой затяжные, это неизбежная ситуация реального инвестирования, при составлении нашего портфеля действительно была допущена ошибка, исправление которой поможет заметно улучшить суммарную доходность. Причем решение в данной ситуации представляется достаточно очевидным — портфель должен состоять из активов, которые ведут себя по возможности независимо друг от друга, хотя каждый по отдельности способен быть источником денежного потока.

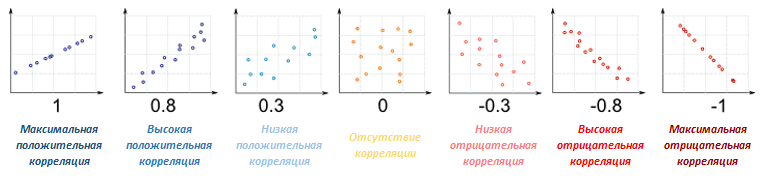
Корреляция описывается числом в интервале от 1 до -1. Единица со знаком плюс означает абсолютно идентичное движение активов (к такой ситуации, например, близки котировки USD/RUB и EUR/RUB), и в этом случае говорят о полной или максимальной положительной корреляции. Минус один описывает полностью противоположенное поведение, когда рост одного актива всегда вызывает убыток другого — это максимально отрицательная корреляция. Оба варианта скорее идеальные случаи, так что отрицательной корреляцией считается любое негативное значение.

Значение около нуля говорит об отсутствии зависимости между котировками. Т.е. в общем корреляция рассчитывается на основании эмпирических данных — подобная функция есть в Экселе — и поэтому зависит от интервала рассмотрения активов. Корреляция финансовых инструментов имеется как на форекс, так и на фондовом рынке — рассмотрим их отдельно.

Корреляция на рынке форекс

На форекс представлено не такое уж большое число значимых соотношений — семь главных валютных пар уже охватят около 80% валютного рынка. Однако при хаотичном изменении котировок говорить о каком-то постоянном значении коэффициента корреляции валютных пар не приходится — оно полностью зависит от выбранного диапазона. Для иллюстрации этого подойдут две ссылки. Вот первая https://www.home.saxo/insights/tools/fx-correlations-table/tool-details :

Как видно, на настоящий момент тут можно оценить коэффициенты корреляции почти за три года. Причем над таблицей слева находится ползунок, перемещая который можно увидеть, как менялась корреляция валютных пар с периода отсчета (сейчас это 17 ноября 2012) до произвольной даты в течение последнего года. При перемещении этого ползунка будет заметно, что ряд валют не только сильно меняет свое значение, но порой изменяется и сам знак корреляции.

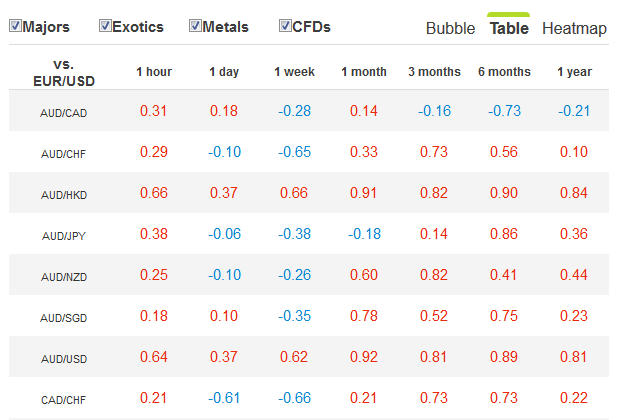
Аналогично можно выбрать периоды за последние 30 и 90 дней — почти наверняка многие показатели в ячейках не будут иметь ничего общего с прежними значениями. Кроме того, очень наглядно корреляция на форекс показана здесь: https://www1.oanda.com/lang/ru/forex-trading/analysis/currency-correlation :

Видно, что в большинстве случаев в течение года валютные пары меняли не только величину, но и знак корреляции к выбранной для сравнения паре (евро/доллар) на противоположенный. Щелчком по другой валютной паре в таблице можно выбрать ее в качестве эталона сравнения.

Корреляция на фондовом рынке

Переходя к фондовому рынку, в первую очередь необходимо обратить внимание на несравненно большее число инструментов, поскольку в принципе каждую акцию (и облигацию) можно рассматривать как отдельный актив. Таблица корреляции каждой акции друг к другу только на американском рынке привела бы к совершенно астрономическим цифрам — слава богу, в распоряжении инвестора есть такой инструмент как ETF, который помогает вложиться в произвольный индекс, отражающий экономику целого государства или даже региона, например Европы.

ETF позволяет широко диверсифицировать капитал — например, биржевой фонд с тикером SPY включает в себя 500 акций компаний США. Но не менее важным является то, что имея простой инструмент для вложения мы можем сравнить индексы различных стран друг с другом (пример — американский S&P500, российский РТС, немецкий DAX и др.) и на выходе получить относительную простую таблицу с достаточно ясными возможностями для инвестирования.

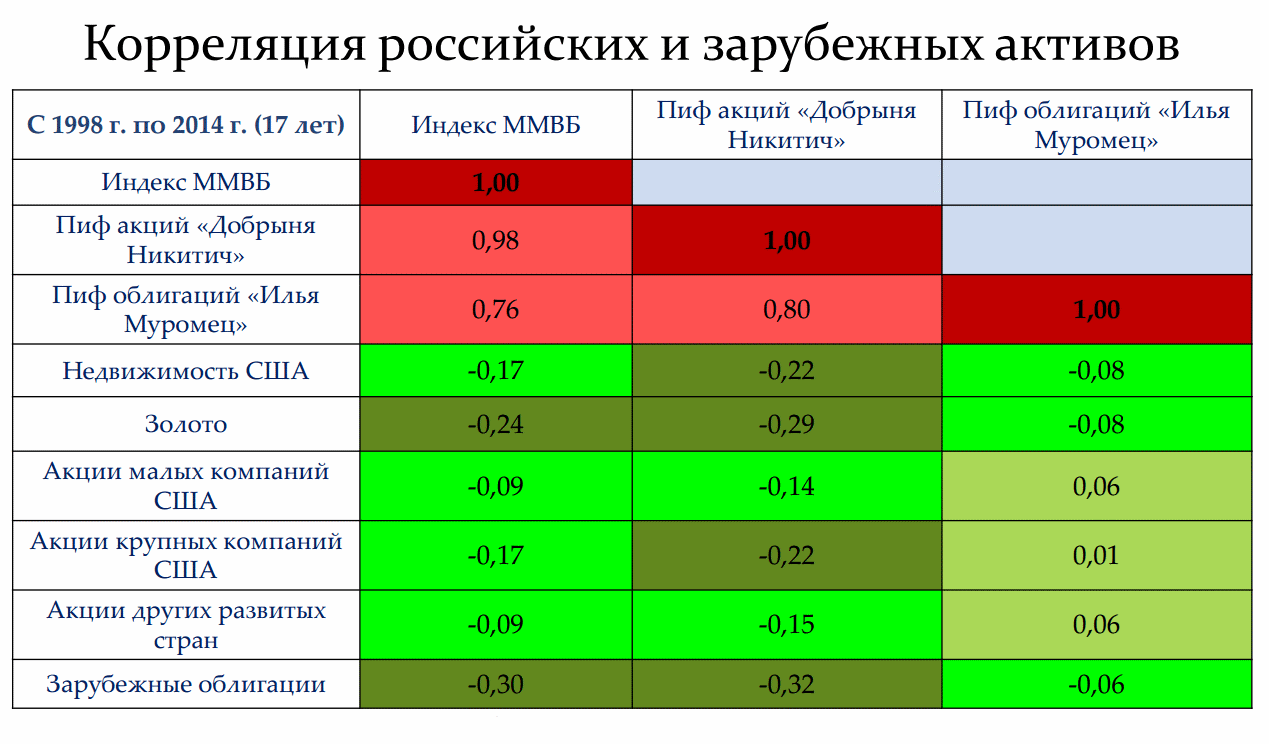
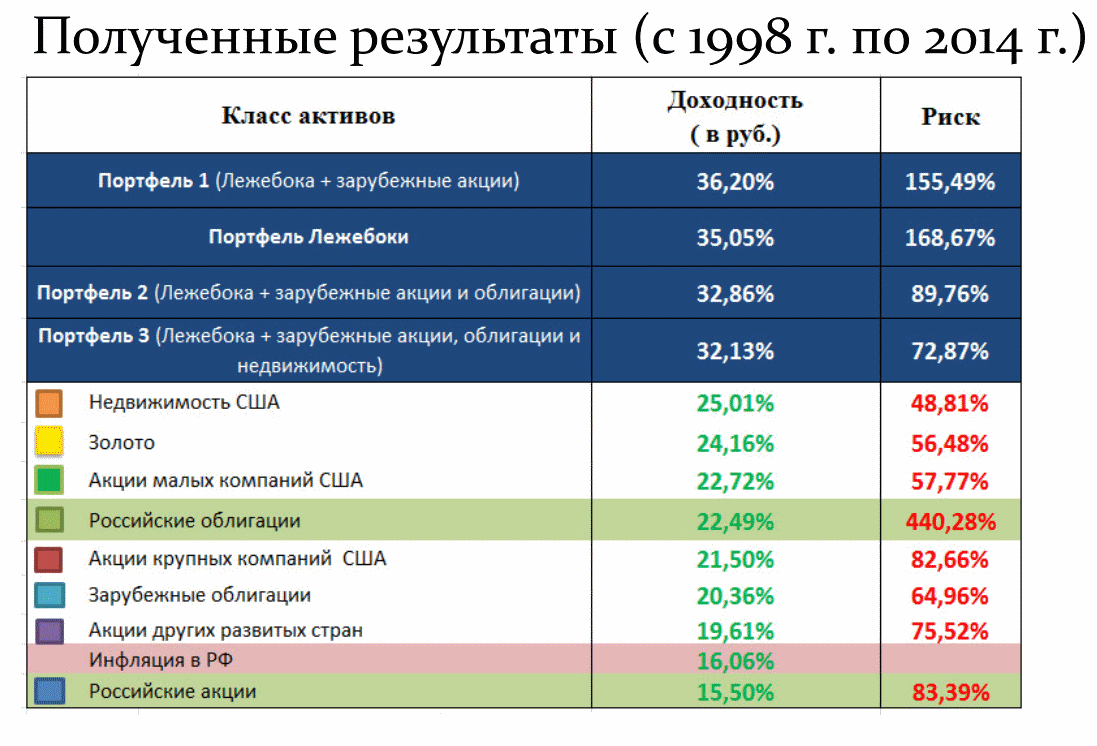
Ложка (и немалая) дегтя в том, что и на фондовом рынке коэффициенты корреляции финансовых инструментов не отличаются постоянством. Однако, в отличие от валютных пар, эти изменения обычно происходят медленнее и находятся в менее широком диапазоне (как будет показано ниже, историческая корреляция американских акций и облигаций с 1930 года описывалась интервалом от +0.5 до -0.5). Рассмотрим корреляцию российских и зарубежных активов (расчеты Сергея Наумова):

Здесь приведена корреляция российских и зарубежных активов на периоде в 17 лет до 2014 года. Из нее видно, что например российские акции и облигации имеют высокую корреляцию друг с другом (их котировки движутся как правило в одном направлении), тогда как золото и зарубежные облигации имели к российским акциям скорее противоположенное движение, т.е. отрицательную корреляцию.

Следовательно, разбавляя американские активы российскими с включением доли золота, можно было бы на первый взгляд добиться сглаживания доходности — однако на практике мы получили бы не просто более ровную кривую, а заметный дополнительный бонус. Посмотрим на таблицу ниже:

Так называемый «портфель лежебоки» — это портфель, включающий равные доли российских акций, облигаций и золота. При этом сравнивая доходность всех четырех портфелей можно увидеть, что она оказалась заметно выше, чем просто арифметическое среднее активов по отдельности! Как такое возможно?

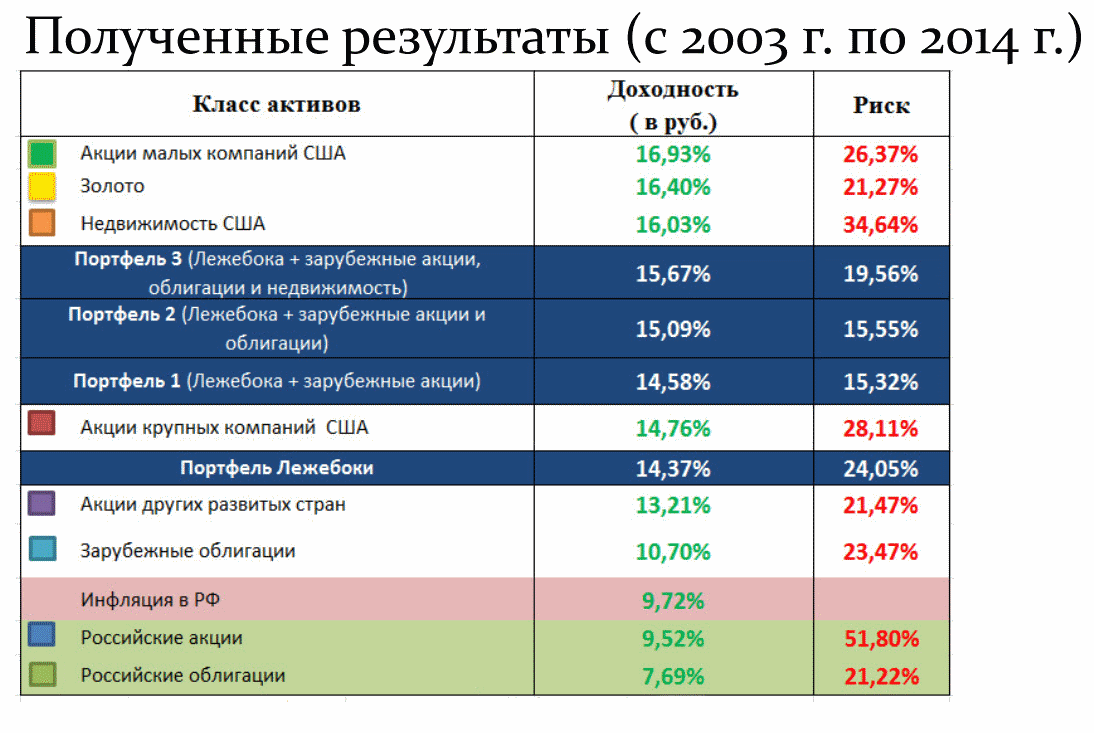
Объяснение этому было дано еще в начале 50-х годов Г. Марковицем, который 30 лет спустя получил за свою теорию Нобелевскую премию — а сама теория стала основой портфельного инвестирования, наряду с понятием о корреляции активов. Согласитесь, что получать в течение 17 лет доходность на уровне 35% в год не позволяет ни один банк — такие предложения делаются лишь откровенными пирамидами. Тем не менее следующий слайд, берущий те же активы, но за другой период, хорошо иллюстрирует высказывание, как прошлая доходность не гарантирует будущей:

Как видно, здесь доходность портфелей представляет уже скорее среднее значение, хотя и лежащее гораздо ближе к верхней границе, чем к нижней; причем риски в этом случае оказываются ниже, чем в прошлой таблице. Откуда такие расхождения? В плане доходности стоит вспомнить огромный рывок российского рынка в 1999 году, когда паи облигаций выросли на невероятные 1800% — и вплоть до 2008 года российский рынок почти непрерывно рос, давая по несколько десятков процентов годовых.

Основной пик пришелся именно на 1999-2000 год. Однако после кризиса 2008 года последовала почти обратная ситуация — несколько восстановившись в 2009 году, в следующие годы даже рублевый индекс ММВБ не сумел достичь своего максимума, а номинированный в долларах РТС и вовсе после декабря 2014 отправился почти к уровню просадки 2008 года. Следовательно, несмотря на отрицательную корреляцию к американскому, российский рынок просто оказался не самым удачным активом, который с 2003 по 2014 годы показал среднюю доходность даже чуть ниже инфляции.

И это является важным фактором, который необходимо учесть — только нулевая или отрицательная корреляция не обеспечит кумулятивный эффект, если хотя бы один из активов будет показывать стагнацию или тем более негативную доходность. Идея именно в том, что в целом доходны оба актива, но проявляется это в разные периоды времени. Поэтому если в качестве развивающегося рынка в дополнение к американскому и европейскому добавлять российские активы, то нужно иметь в виду, что должный эффект, показанный в первой таблице, проявится лишь в случае возобновления роста.

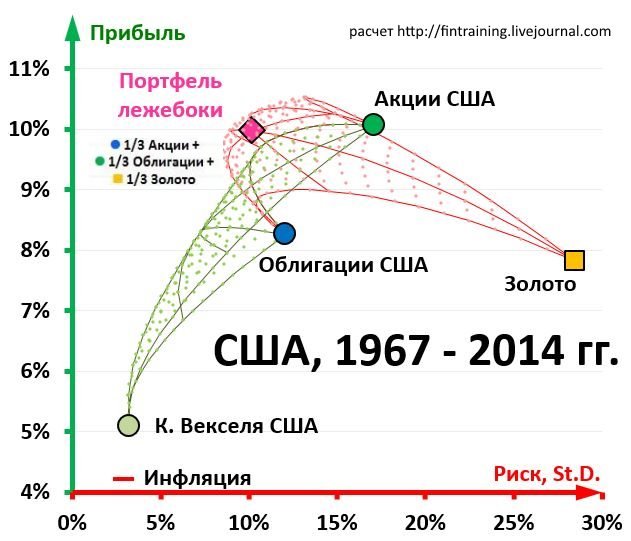
Следовательно, нужно не только учитывать корреляцию, но и в идеальном случае представлять экономические возможности своих активов. При этом на американском рынке аналогичный портфель за почти 50 лет показал те же результаты, что и акции, однако с заметно меньшим риском:

Если же рассмотреть те же данные с 1925 года, то картина немного изменится: хотя доходность по акциям останется почти на том же уровне (9%, т.е. только на 10% меньше), но золото даст результат, близкий к 5% (что меньше почти на 40%). Соответственно, пострадает и портфельный результат: американский «лежебока» с 1925 года даст доходность лишь немногим более 7%, уже заметнее уступая акциям. Поэтому вывод ожидаем: волшебного портфеля нет, а российский лежебока в ближайшие годы скорее всего будет постепенно терять свой громадный отрыв, приближаясь к средним рыночным значениям.

Зависимость корреляции от времени

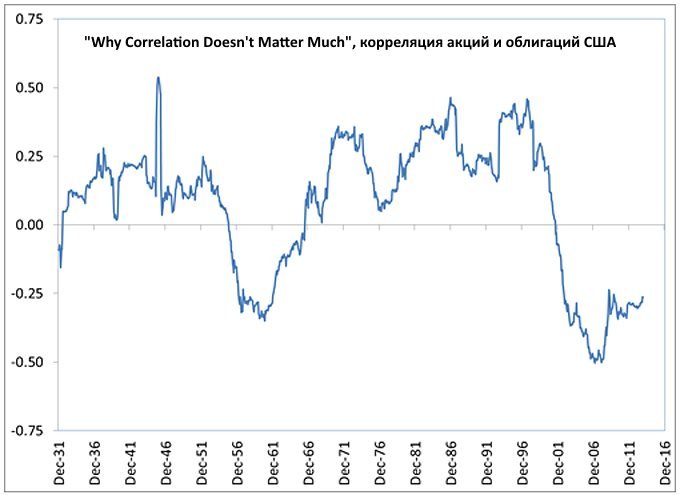
Как уже упоминалось выше, корреляция не является константой и сама меняется в зависимости от времени. К примеру, корреляция между акциями США и пятилетними гос. облигациями с 1926 по 2013 годы была равна 0.07 — т.е. зависимость почти не прослеживалась. Однако на истории корреляция колебалась от -0,5 до +0,5, причем в XX веке после Великой Депрессии она находилась в отрицательной зоне лишь с середины 50-х по середину 60-х годов. В период с 1970-1985 корреляция акций и облигаций была равна 0.3%, тогда как с 2002-2013 обратной по знаку:

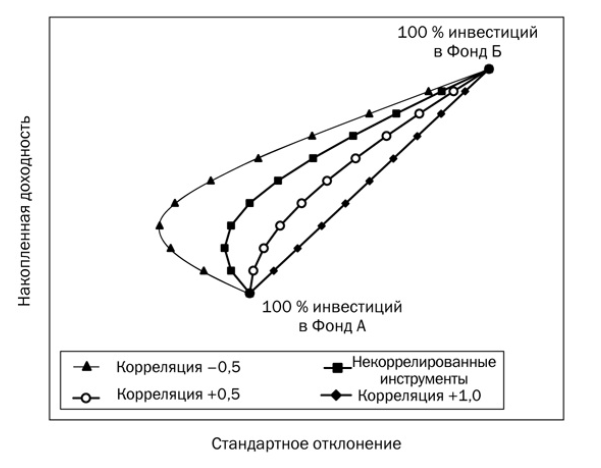
Таким образом, задача поиска доходности зависит от двух неизвестных: корреляции и доходности активов на рассматриваемом промежутке, причем эта доходность достигается с различным риском (отклонением от среднего значения). Отрицательная корреляция в общем случае позволяет достигать большей доходности с меньшим риском по сравнению с менее доходным активом:

Фонд А — менее волатильный и менее доходный актив (облигации), фонд Б — более волатильный и доходный (акции). Стандартное отклонение определяет размах колебаний относительно среднего значения актива. Такое соотношение, как на рисунке выше, наблюдается на длинной истории — однако в пределах десятилетий может довольно сильно меняться:

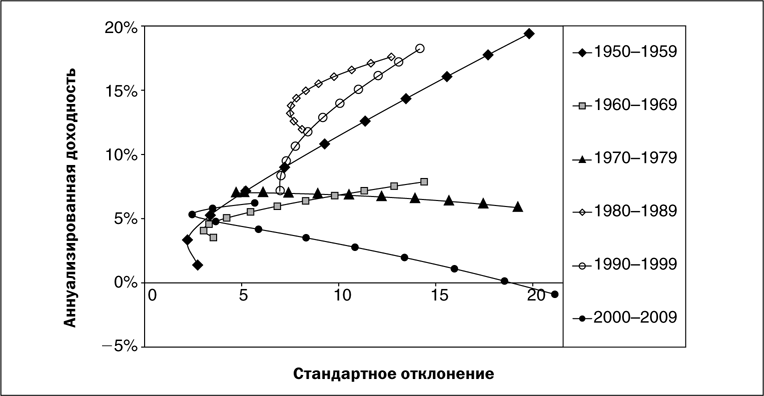
Видно, что на протяжении 2000-2009 годов американские акции даже ушли в минус, в результате чего кривая получила движение вниз, а не вверх. Следовательно, корреляция ничего не говорит об абсолютной доходности — первая может мало меняться на протяжении 20 лет, однако результаты одинаковых портфелей на следующих друг за другом 10-летних промежутках разойдутся.

Так, в кризисные 70-е и растущие 80-е корреляция американских акций и 5-летних облигаций была в среднем одинакова (около 0.25), однако доходность портфеля 50 на 50 во втором случае была 15% годовых, а в первом лишь около 7%. Ниже отдельно показаны наилучшее и наихудшее американское десятилетие с 1950 года:

Как видим, отрицательная корреляция с 2000 года явилась причиной заметного выгиба кривой влево, в результате чего 5% доходности могли быть достигнуты с очень низким риском. Несомненно важным для инвестора является и корреляция других активов — в первую очередь американского и европейского рынков, стран Азии и пр. Детальный подход показывает разницу в их движениях — и следовательно, необходимость учитывать в своем портфеле рынки разных стран.

Источник

Расчет коэффициента корреляции

Методы расчета коэффициента корреляции

При изучении различных социально-экономических явлений выделяют функциональную связь и стохастическую зависимость. Функциональная связь — это такой вид связи, при которой некоторому взятому значению факторного показателя соответствует лишь одно значение результативного показателя. Функциональная связь проявляется во всех случаях исследования и для каждой определенной единицы анализируемой совокупности.

Размещено на www.rnz.ru

В том случае, когда причинная зависимость действует не в каждом конкретном случае, а в общем для всей наблюдаемой совокупности, среднем при значительном количестве наблюдений, то такая зависимость является стохастической. Частным случаем стохастической зависимости выступает корреляционная связь, при которой изменение средней величины результативного показателя вызвано изменением значений факторных показателей. Расчет степени тесноты и направления связи выступает значимой задачей исследования и количественной оценки взаимосвязи различных социально-экономических явлений. Определение степени тесноты связи между различными показателями требует определение уровня соотношения изменения результативного признака от изменения одного (в случае исследования парных зависимостей) либо вариации нескольких (в случае исследования множественных зависимостей) признаков-факторов. Для определения такого уровня используется коэффициент корреляции.

Линейный коэффициент корреляции был впервые введен в начале 90-х гг. XIX в. Пирсоном и показывает степень тесноты и направления связи между двумя коррелируемыми факторами в случае, если между ними имеется линейная зависимость. При интерпретации получаемого значения линейного коэффициента корреляции степень тесноты связи между признаками оценивается по шкале Чеддока, один из вариантов этой шкалы приведен в нижеследующей таблице:

Шкала Чеддока количественной оценки степени тесноты связи

Источник