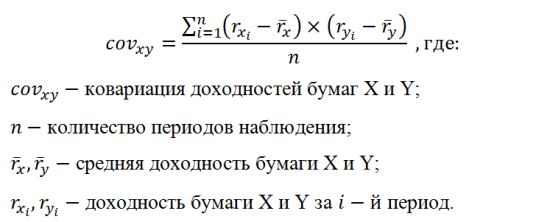Коэффициент корреляции доходность рыночного портфеля

5 ключевых метрик инвестиционного портфеля

Чем большую доходность хочет инвестор, тем более рисковые инструменты ему придется использовать. Задача инвестора — найти такое сочетание активов, при котором соотношение доходности и риска станет наилучшим.

Рассмотрим 5 ключевых метрик, которые помогут в этом. Эти параметры выдает большинство сервисов для анализа ценных бумаг и портфелей, в частности сайт Portfolio Visualizer, о работе с которым у нас есть статья.

📈 Среднегодовая доходность (CAGR)

Показывает среднегодовой темп роста портфеля на основе стартового и конечного капитала, а также срока инвестирования. Это среднегеометрическая доходность, учитывающая сложный процент, в отличие от средней арифметической доходности.

CAGR подходит, если инвестор не пополняет портфель и не выводит из него деньги в течение срока инвестирования. Если есть движение средств, то лучше использовать IRR — внутреннюю норму доходности

⏩ Стандартное отклонение (st. dev., σ)

Показывает, насколько волатильна доходность портфеля, то есть насколько он рискован. Считается как квадратный корень из дисперсии — разброса значений доходности от ее среднего значения.

Чем выше стандартное отклонение доходности актива или портфеля, тем выше риск. Чтобы снизить риск, в портфеле стоит сочетать инструменты с низким коэффициентом корреляции — о нем далее

🌀 Корреляция (correlation)

Показывает, насколько похоже ведут себя инструменты. Коэффициент корреляции может быть в диапазоне от −1 до 1.

Корреляция, близкая к единице, говорит о тесной взаимосвязи двух активов. Значение, близкое к нулю, показывает, что явной связи нет, а при значении около −1 активы движутся разнонаправленно.

Чем ниже коэффициент корреляции, тем лучше активы дополняют друг друга в портфеле. В теории, взяв два актива с корреляцией −1, можно достичь нулевого риска портфеля

🅱️ Бета (beta, β)

Показывает, как отдельный актив или портфель ведут себя относительно рынка. В случае с американскими акциями бета рассчитывается относительно индекса S&P 500, в случае с российскими акциями — относительно индекса Мосбиржи.

Бета 1 значит, что актив идентичен рынку. Если более 1, то актив коррелирует с рынком, но ведет себя более волатильно: сильнее растет или сильнее падает. Если бета от 0 до 1, то актив движется однонаправленно с рынком, а риск меньше рыночного.

При бете от 0 до −1 актив и рынок движутся в разные стороны, а актив стабильнее. При бете меньше −1 актив и рынок тоже движутся разнонаправленно, но актив волатильнее

💼 Коэффициент Шарпа (Sharpe ratio)

Показывает эффективность портфеля с точки зрения доходности и риска.

Считается так: (Доходность портфеля − Безрисковая процентная ставка) / Стандартное отклонение. Безрисковая ставка — это, например, доходность вкладов или векселей казначейства США.

Чем выше коэффициент Шарпа, тем большую прибыль извлекает инвестор на единицу риска и тем эффективнее стратегия

Источник

Коэффициент корреляции | Correlation coefficient

В статистике коэффициент корреляции (англ. Correlation Coefficient) используется для проверки гипотезы о существовании зависимости между двумя случайными величинами, а также позволяет оценить ее силу. В портфельной теории этот показатель, как правило, используется для определения характера и силы зависимости между доходностью ценной бумаги (актива) и доходностью портфеля. Если распределение этих переменных является нормальным или близким к нормальному, то следует использовать коэффициент корреляции Пирсона, который рассчитывается по следующей формуле:

— среднеквадратическое (стандартное) отклонение доходности i-ой ценной бумаги;

— среднеквадратическое (стандартное) отклонение доходности портфеля.

В расширенном виде формулу коэффициента корреляции Пирсона можно записать следующим образом:

где k_i – доходность ценной бумаги в i-ом периоде;

— ожидаемая (средняя) доходность ценной бумаги;

p_i – доходность портфеля в i-ом периоде;

— ожидаемая (средняя) доходность портфеля.

n – количество наблюдений.

Свойства коэффициента корреляции

Значение коэффициента корреляции изменяется от -1 до +1. Его отрицательное значение говорит о том, что между переменными наблюдается обратная взаимосвязь. Например, когда доходность ценной бумаги будет расти, то доходность портфеля будет падать, и наоборот. Положительное значение свидетельствует о прямой взаимосвязи, то есть, если доходность ценной бумаги будет расти, доходность портфеля также будет расти, и наоборот.

Если абсолютное значение коэффициента корреляции находится ближе к 1, то это свидетельствует о сильной взаимосвязи между переменными, а если ближе к 0 — то это говорит о слабой связи или ее отсутствии. Если его значение равно -1 или +1, то можно говорить о существовании функциональной взаимосвязи между переменными, то есть одну из них можно выразить через другую посредством математической функции.

Пример расчета

Динамика доходности акций Компании А и Компании Б, а также динамика доходности портфеля ценных бумаг выглядят следующим образом:

Чтобы использовать формулу коэффициента корреляции Пирсона необходимо рассчитать среднюю доходность, которая составит:

• для акций Компании А 4,986%;
• для акций Компании Б 5,031%;
• для портфеля 3,201%.

Ковариация доходности акций Компании А и портфеля составит -0,313, а акций Компании Б и портфеля 0,242. (О том, как рассчитывается ковариация доходности можно прочитать здесь)

Среднеквадратическое отклонение доходности акций Компании А составит 0,6398, акций Компании Б 0,5241 и портфеля 0,5668. (О том, как рассчитывается среднеквадратическое отклонение можно прочитать здесь)

Коэффициент корреляции доходности акций Компании А и доходности портфеля составит -0,864, а акций Компании Б 0,816.

R_Б = 0,242/(0,5241*0,5668) = 0,816

Можно сделать вывод о присутствии достаточно сильной взаимосвязи между доходностью портфеля и доходностью акций Компании А и Компании Б. При этом, доходность акций Компании А демонстрирует разнонаправленное движение с доходностью портфеля, а доходность акций Компании Б однонаправленное движение.

Источник

Акции (урок 4) – диверсификация: коэффициент корреляции

Продолжаем развивать общий подход к вложениям в акции.

В прошлых уроках мы разобрались с диверсификацией по трём параметрам:
— sector
— cyclical / non-cyclical
— capitalization

Теперь, как только мы слышим какое-то новое имя, мы прежде всего сразу смотрим:

а) к какому сектору принадлежит компания
б) какая у неё капитализация.

Прежде чем двигаться дальше, еще немного задержусь на диверсификации. Здесь мне придётся разжевать очень базовые вещи.

Допустим ваш портфель состоит пока всего лишь из одного инструмента (это акции одной компании). Чтобы оценить, насколько хорошо ваш портфель «разбавит» (или диверсифицирует) добавление в него второго инструмента, надо посмотреть на так называемый коэффициент корреляции между первым и вторым инструментами.

Коэффициент корреляции – это такой математический показатель, который колеблется от -1 до 1. Для подсчёта коэффициента корреляции есть специальная формула, но её я приводить не буду, т.к от эконометрики я в своё время очень устал. Просто посмотрите в tradingview.com. Там среди индикаторов есть в готовом виде correlation coefficient. Это один из немногих индикаторов, которые я использую в торговле (а их я использую очень мало):

▫️+1 означает, что инструменты «ходят вместе»: если А растёт на 1%, то B растёт тоже на 1%.
▫️0 означает полное отсутствие взаимосвязи.
▫️-1 означает совершенную отрицательную взаимозависимость, т.е. если инструмент А падает на 1%, то инструмент B растёт на 1%.
▫️+0.4, к примеру, означает умеренно-положительную взаимозависимость, но некоторый эффект диверсификации всё же будет присутствовать.

Если вы добавите в свой портфель второй инструмент, у которого корреляция с первым инструментом равна +1, то это ничуть не диверсифицирует ваш портфель, т.е. вы поступите тупо (так и продолжите держать все яйца в одной корзине).

Коэффициент корреляции — очень и очень используемый математический показатель в сфере управления активами, запомните его.

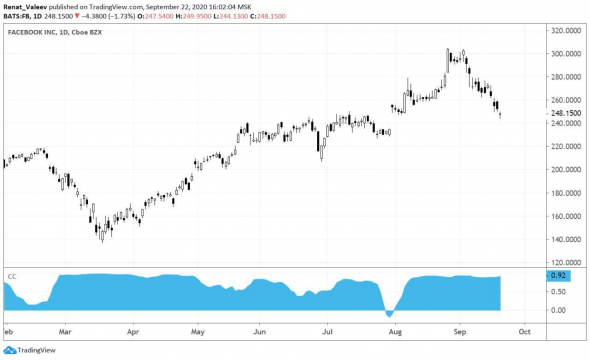
На картинке ниже – график Facebook. Внизу под ним коэффициент корреляции с индексом S&P 500. Видно, что Facebook очень хорошо коррелирует с индексом (коэффициент почти всегда в положительной зоне и равен единице), то есть они повторяют движения друг друга.

Если взять золото, то его корреляция с S&P уже не так сильна. Однако золото тоже часто ходит вместе с S&P.

Кстати, для подсчёта корреляции могут использоваться дневные значения, 4-х часовые, 1-часовые, минутные, в общем, какие угодно…

Как видите, инвестирование в акции – это целый океан. Сегодня 4-й урок, а мы еще даже не спустились на уровень анализа отдельных компаний.

Поймите очень простую, но важную истину: инвестирование в акции – это не только выбор отдельных компаний. Это прежде всего управление портфелем с учетом взаимосвязей входящих в него инструментов.

И как мы увидим дальше, диверсификация бывает очень и очень обманчива… Она может усыпить бдительность инвестора.

Источник

Что такое корреляция акций и облигаций?

Объясните, пожалуйста, простым языком, что такое корреляция ценных бумаг? Почему о ней говорят при составлении портфеля и что значит, когда она отрицательная?

Корреляция показывает, насколько активы схожи по поведению. Показатель описывает закономерности. Например, если при росте одного актива другой дешевеет и эта закономерность подтверждается историческими данными, говорят, что у активов обратная корреляция. Это относится как к отдельным ценным бумагам, так и к широким рынкам, классам активов и секторам экономики.

Коэффициент корреляции вычисляется на конкретном историческом отрезке. Он обозначается буквой r и принимает значения от −1 до +1. Если два актива движутся в связке, то коэффициент корреляции будет ближе к +1, а если в противоположных направлениях — ближе к −1. Но когда корреляция близка к нулю, взаимосвязи между ними нет. Это значит, что при росте или падении одного актива другой может вообще никак себя не проявлять. Например, корреляция акций и облигаций на рынке США в период с 1950 по 2012 год составила 0,11.

Расскажу, как можно использовать знание о корреляции при формировании портфеля.

Роль корреляции в управлении портфелем

Понимание корреляции между инструментами позволяет диверсифицировать портфель и снизить инвестиционные риски.

Например, если инвестор собрал портфель из 10 нефтегазовых компаний, он защитил себя только от специфических рисков, связанных с конкретным эмитентом. Волатильность портфеля по-прежнему будет высокой: если цены на нефть упадут, портфель также уйдет в красную зону из-за тесной корреляции акций.

Чтобы диверсификация работала, необходимо использовать инструменты с низкой или обратной корреляцией. Тогда движение цены одного актива будет компенсироваться движением другого. Так, государственные облигации — наиболее частный диверсификатор для акций, поскольку у этих активов исторически низкая взаимосвязь друг с другом.

Таким же образом устроен и механизм хеджирования, когда инвестор открывает позицию с отрицательной корреляцией к исходному активу, чтобы застраховаться от его падения. Например, так называемые обратные ETF обладают корреляцией, близкой к −1 по отношению к исходному активу.

Источник

Инвестиционный портфель. Доходность и риск инвестиционного портфеля.

Понятие инвестиционного портфеля.

Инвестиционный портфель представляет собой целенаправленно сформированную в соответствии с определённой инвестиционной политикой и выбранной управленческой стратегией совокупность вложений в различные инвестиционные объекты.

Процесс формирования эффективного портфеля инвестиций, отвечающего возложенным на него ожиданиям, состоит из шести основных этапов.

• Первый этап, заключается в формулировании чётких инвестиционных целей, относительно совокупной ожидаемой и желаемой доходности инвестиционных вложений, максимально допустимого и предпочтительного уровня инвестиционного риска, а также требуемой ликвидности инвестиционных объектов. Альтернативность рассмотренных целей обуславливает выбор приоритетных или сбалансированных показателей служащих критерием при выборе инвестиционных инструментов.
• Второй этап направлен на формирование инвестиционной политики фиксирующей предпочтения относительно типов ценных бумаг, из которых предполагается формирование портфеля, секторов к которым должны относить приобретаемые бумаги, учёт действующих законодательных ограничений и прочих факторов.
• Третий этап заключается в выборе активной или пассивной модели управления инвестиционным портфелем исходя из наиболее приоритетных целей.
• Четвёртый этап подразумевает основывающийся на фундаментальном, техническом и портфельном анализе, подбор ценных бумаг, отвечающих определённым в процессе первого этапа критериям.
• Пятый этап предусматривает деятельность по управлению уже сформированным инвестиционным портфелем, направленную на сохранение первоначальных вложений и обеспечение общей целевой направленности портфеля.
• Шестой этап ориентирован на оценку эффективности управления портфелем инвестиций одним из наиболее объективных методов.

Доходность инвестиционного портфеля.

Главными параметрами при формировании и управлении инвестиционным портфелем, являются его ожидаемая доходность и риск. В связи с отсутствием возможности точного определения бедующей динамики вышеуказанных параметров, данные величины оцениваются, в первую очередь, на основе статистической информации за предыдущие периоды времени.

Ожидаемая доходность портфеля рассчитывается на основе ожидаемой доходности содержащихся в нём активов двумя способами.

Первый состоит в том, чтобы на основе прошлых статистических данных доходности актива рассчитать её среднеарифметическое значение по следующей формуле: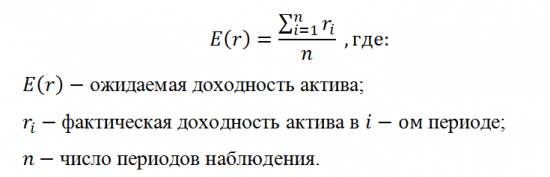

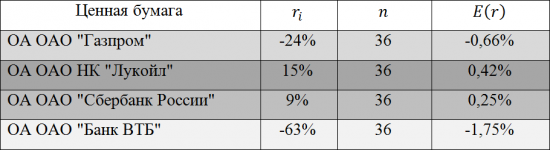
В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности для 4 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка, на основании их ежемесячных доходностей за последние три года.

Из полученных значений следует, что наиболее привлекательной ценной бумагой являются обыкновенные акции ОАО НК «Лукойл», с ожидаемой доходностью в расчёте на месяц в 0,42%.

Второй заключается в учёте возможного будущего вероятностного распределения доходности актива. Ожидаемая доходность актива определяется как среднеарифметическая взвешенная, где весами являются вероятности каждого события, которые в сумме должны составлять 100% и рассчитывается по следующей формуле: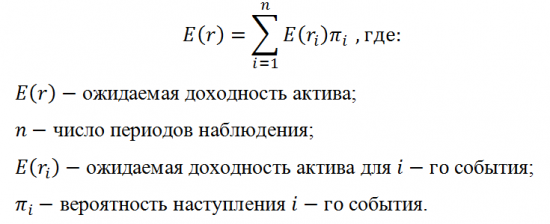

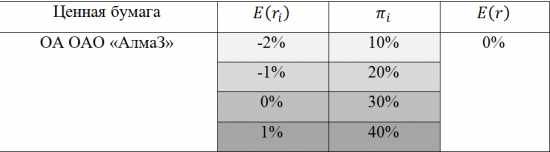
В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности несуществующей ценной бумаги.

Из полученного значения следует, сто ожидаемая доходность ОА ОАО «АлмаЗ», равна 0%.

Ожидаемая доходность инвестиционного портфеля при невозможности заимствования средств или осуществления коротких продаж.

Формируемый инвестиционный портфель состоит из нескольких ценных бумаг, каждая из которых обладает своей ожидаемой доходностью, среднеарифметическая ожидаемая доходность которых, является ожидаемой доходностью инвестиционного портфеля и рассчитывается по следующей формуле:

Удельный вес n-ой бумаги в портфеле рассчитывается, как отношение её стоимости к стоимости всего портфеля по следующей формуле:

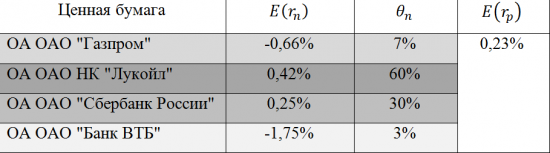
В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности инвестиционного портфеля состоящего из 4 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка, на основании их ежемесячных доходностей за последние три года.

Из полученного в ходе расчётов значения следует, что ожидаемая доходность состоящего из вышеуказанных 4 ценных бумаг инвестиционного портфеля, равна 0,23%.

Ожидаемая доходность инвестиционного портфеля при возможности заимствования средств.

Формирование инвестиционного портфеля может осуществляться не только на собственные средства, но и на заёмные, в результате чего, возникает эффект финансового рычага и увеличивается ожидаемая доходность портфеля. В этом случае, денежные средства занимаются под более низкую процентную ставку и размещаются в потенциально более доходный актив, образуя портфель, состоящий фактически из двух активов, приобретаемой ценной бумаги и заимствованных средств. Ожидаемая доходность портфеля рассчитывается по следующей формуле:

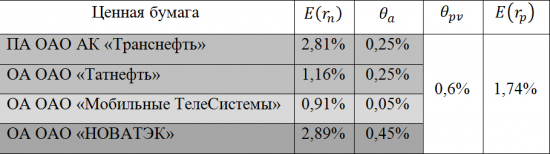
В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности инвестиционного портфеля состоящего из 4 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка, на основании их ежемесячных доходностей за последние три года. В качестве заёмных средств будем использовать краткосрочный кредит (сроком на 1 месяц) с простой процентной ставкой заимствований, равной 12 процентам годовым.

Из полученных в ходе расчётов значений следует, что ожидаемая доходность инвестиционного портфеля составила 1,74 процента. За счёт привлечения заёмных финансовых ресурсов, доходность портфеля была увеличена на 0,8 процента, что говорит об эффективности использования заёмных средств, в формировании инвестиционного портфеля.

Ожидаемая доходность инвестиционного портфеля при использовании только заёмных средств.

Формирование инвестиционного портфеля может осуществляться исключительно за счёт заёмных средств, что имеет только теоретическое значение, поскольку получение кредита связано с определённым обеспечением полученных средств. Поэтому ожидаемый результат необходимо оценивать относительно тех средств, которые в этом случае блокируются.

Ожидаемая доходность портфеля с использованием только заёмных средств рассчитывается по следующей формуле:

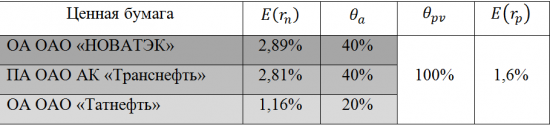
В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности инвестиционного портфеля состоящего из 3 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка. Расчёт будет вестись на основании их ежемесячных доходностей за последние три года, а доля заёмных средств в инвестиционном портфеле, будет составлять 100 процентов.

Из полученных в ходе расчётов значений следует, что путём выбора инвестиционных объектов с наибольшими ожидаемыми доходностями возможно формирование инвестиционного портфеля за счёт только заёмных средств, а также рассчитывать на получение дохода от подобной операции. Так, ожидаемая доходность используемого в данном примере инвестиционного портфеля, составила 1,6 процента.

Ожидаемая доходность инвестиционного портфеля при возможности коротких продаж.

Формирование инвестиционного портфеля может осуществляться с использованием короткой продажи занятого у брокера актива без процентов и резервирования средств, по обеспечение другими активами, находящимися в инвестиционном портфеле. Ожидаемая доходность портфеля в данном случае, будет рассчитываться по следующей формуле:

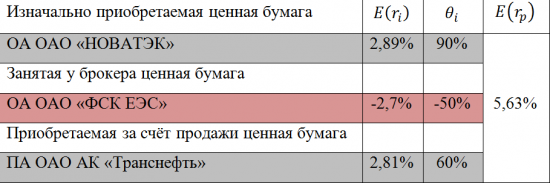
В качестве примера использования данного способа, осуществим расчёт ожидаемой доходности инвестиционного портфеля состоящего из 4 ценных бумаг входящих в состав «голубых фишек» российского фондового рынка. Расчёт будет вестись на основании их ежемесячных доходностей за последние три года, а доля занятых у брокера ценных бумаг будет равна 30% стоимости портфеля. Также, в данном примере, брокер не взимает процентов за предоставленные ценные бумаги и не резервирует часть средств, в качестве их обеспечения.

Из полученных в ходе расчёта значений следует, что использование занятых у брокера и предназначенных для продажи ценных бумаг, позволило увеличить ожидаемую доходность инвестиционного портфеля до 5,63 процентов. На практике, допускается продажа заёмных ценных бумаг в том случае, если их ожидаемая доходность не превышает доходности приобретаемых ценных бумаг. В противном случае, велик риск получения убытков от данной операции.

Риск инвестиционного портфеля

Основополагающими мерами риска финансового актива являются такие показатели как стандартное отклонение (волатильность) и дисперсия его доходности, которые говорят о степени возможного разброса фактической доходности вокруг его средней доходности. Данные показатели можно определить на основе прошлых статистических данных доходности актива.

Дисперсия является показателем рассеяния фактических значений доходности акции вокруг её средней доходности и рассчитывается по следующей формуле:

Однако, размерность дисперсии представляет собой квадрат доходности ценной бумаги. Если в формуле учитывается доходность в процентах, а размерность дисперсии, это процент в квадрате, поэтому показателем такой размерности не всегда удобно пользоваться. Поэтому из дисперсии извлекают корень и получают стандартное отклонение последующей формуле: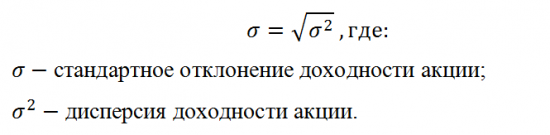

В отличие от ожидаемой доходности инвестиционного портфеля его риск не является средневзвешенной величиной стандартных отклонений доходностей содержащихся в нем ценных бумаг. Данное несоответствие связанно с различной реакцией ценных бумаг на изменение рыночной конъюктуры, в результате чего, стандартные отклонения доходности различных ценных бумаг в ряде случаев будут погашать друг друга, что приведёт к снижению риска инвестиционного портфеля. В связи с этим, при подборе ценных бумаг в портфель инвестиций принято определять степень их взаимосвязи на основании значений ковариации и коэффициента корреляции.

Ковариация показывает зависимость между двумя ценными бумагами и может быть:

• положительной — характеризующейся однонаправленным изменением доходностей ценных бумаг;
• отрицательной — говорящей о противоположном изменении доходностей ценных бумаг;
• нулевой — отражающей отсутствие зависимости между ценными бумагами.

Расчёт ковариации осуществляется по следующе формуле:

В качестве примера определения ковариации между ценными бумагами осуществим расчёт помесячной ковариации между 2 ценными бумагами российского фондового рынка. Расчёт проводится на их доходности за последние 8 лет, т.е. с 2006 года. Полный список возможных значений ковариации для ключевых ценных бумаг РФР.

Из полученных значений можно сделать следующие выводы: во всех рассматриваемых временных окнах наблюдается положительная ковариация, свидетельствующая об однонаправленном движении рассматриваемых ценных бумаг.

Коэффициент корреляции отражает степень зависимости двух ценных бумаг. В отличие от ковариации, данный показатель не зависит от единиц измерения доходностей ценных бумаг и не характеризует рассеяние доходностей вокруг средних значений. В результате чего ковариация не позволяет получить наглядное отражение степени взаимосвязи между инструментами.

Данный коэффициент имеет значения в диапазоне от -1 до +1 и рассчитывается по следующей формуле:

В качестве примера, осуществим расчёт данного коэффициента на аналогичных условиях с теми, что использовались при определении ковариации.

Из полученных в ходе расчёта значений следует, что в 91% случаев корреляция является положительной, следовательно, динамика доходностей ценных бумаг является зависимой. В случае снижения котировок одной ценной бумаги, вторая будет следовать за ней.

После определения взаимосвязи меду ценными бумагами путём расчёта ковариации и коэффициента корреляции можно приступить к подбору инвестиционных объектов и определению совокупного риска портфеля, рассчитываемого несколькими способами, ключевые из которых будут далее рассмотрены.

Риск портфеля состоящего из двух активов определяется на основании их ковариации, удельных весов и стандартных отклонений по следующей формуле:

В качестве примера определения риска инвестиционного портфеля состоящего из 2 ценных бумаг, осуществим расчёт риска портфеля состоящего из ОА ОАО «Газпром» и ОА ОАО «Лукойл». Расчёт ожидаемого риска будет проводиться на их ежемесячных доходностях за последние восемь лет.

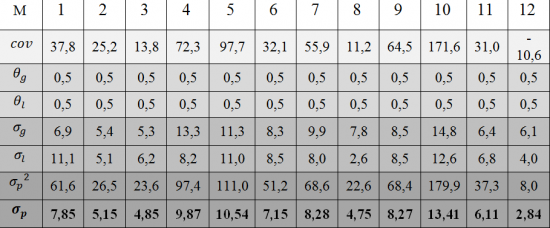
Из полученных значений можно сделать следующие выводы. Первый, наименьший риск инвестиционного портфеля показывают декабрьские вложения (порядка 3 процентов), майские наибольший (10,5 процентов). Второй, наибольшее влияние на риск портфеля оказывает волатильность содержащихся в нём инструментов.

Другой способ расчёта риска портфеля из двух ценных бумаг, применяется в том случае, если корреляция их доходностей равна или близка к значению +1. Таким образом, риск инвестиционного портфеля представляет собой средневзвешенный риск входящих в него ценных бумаг и рассчитывается по следующей формуле: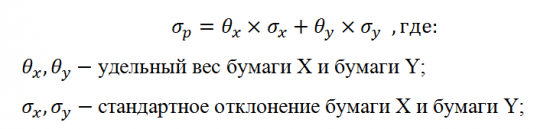

В качестве примера использования данного способа, осуществим расчёт ожидаемого риска на основании доходностей обыкновенных акций ОАО «Банк ВТБ» и ОАО «Сбербанк России», являющихся представителями одного сектора с наибольшей корреляцией доходностей (0,835).

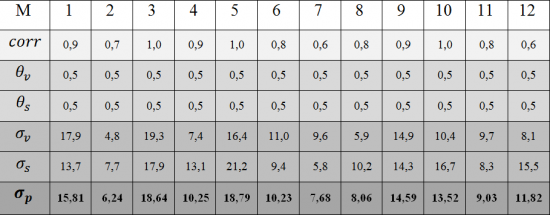
Из полученных значений следует, что в данном случае диверсификация портфеля не привела к сокращению совокупного риска инвестиционного портфеля, а только усреднила его. Следственно, при изменении рыночной конъюктуры доходности ценных бумаг будут изменяться в прямой зависимости в одном и том же направлении.

Третий способ расчёта риска портфеля из двух ценных бумаг применяется в том случае, если значение корреляции их доходностей равно -1 или незначительно больше.

В данном случае, формула расчёта риска портфеля из двух активов с корреляцией + 1 трансформируется в формулу разницы и выглядит следующим образом: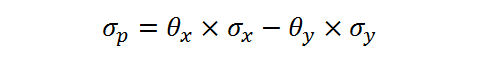

На практике, к тому же на российском фондовом рынке найти инструменты с близкой к -1 отрицательной корреляцией тяжело, а в составе «голубых фишек» таких инструментов вовсе нет, чего нельзя сказать про валютный рынок. Примером подобной отрицательной корреляции может служить валюта США и Японии. За десятилетний период, корреляция между этими валютами составила -0,85.

Объединив в определённой пропорции данные валюты в инвестиционном портфеле, можно добиться безрисковых вложений, также не приносящих инвестиционного дохода и направленных на сохранение капитала и его защиту от валютных рисков.

Наиболее эффективным способом формирования хорошо диверсифицированного инвестиционного портфеля, является распределение капитала между ценными бумагами, значение корреляции между которыми наиболее близко к нейтральному значению.

Риск портфеля из двух активов с отсутствием корреляции между ними, определяется по следующей формуле: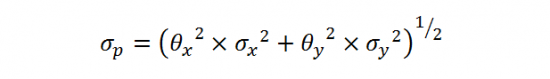

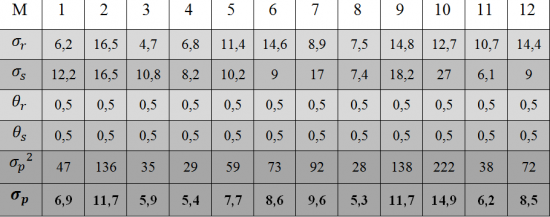
В качестве примера использования данного метода, осуществим расчёт риска инвестиционного портфеля, состоящего из 2 ценных бумаг с наиболее близким к 0 значением корреляции их доходностей. Наиболее подходящими для поставленной задачи, являются обыкновенные акции ОАО «Ростелеком» и ОАО «Северсталь». Совокупная корреляция между их ежемесячными доходностями за последние восемь лет, равна 0,15.

Из полученных в ходе расчётов значений, можно сделать следующий вывод, риск сформированного нами инвестиционного портфеля находится в диапазоне от 5,3% до 14,9%, в зависимости от месяца его ориентировочного формирования. Однако сказать, как на практике поведёт себя одна бумага, по отношению к другой не представляется возможным.

Риск инвестиционного портфеля из нескольких ценных бумаг.

В заключение отражения способов определения риска портфеля, осуществим расчёт риска для инвестиционного портфеля из нескольких ценных бумаг. Осуществлять оценку данного показателя будем на основе ежемесячных доходностей ценных бумаг трёх крупнейших эмитентов. А именно, обыкновенных акций ОАО «Банк ВТБ», ОАО НК «Лукойл» и ОАО «Сбербанк России».

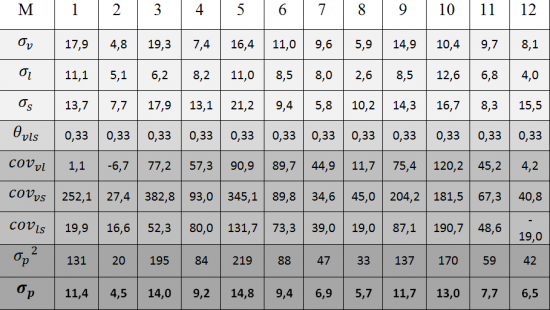
Следует заметить, что приведённые способы оценки таких основополагающих характеристик любого инвестиционного портфеля, как его риск и ожидаемая доходность, являются основополагающими, а не общепринятыми и наиболее эффективными. Как правило, в любой крупной компании, осуществляющей инвестиционную деятельность на рынке ценных бумаг, для оценки этих неотъемлемых качеств портфеля используются собственные методики, характеризующиеся наибольшей точностью оценки.

———База для осуществления расчётов в следующем посте (не вместилась)———

Опираясь на полученные в ходе расчётов значения данных показателей, перед управляющим стоит задача подбора инвестиционных объектов с целью формирования эффективного и целесообразного портфеля. Главной ориентацией которого, является наибольшая ожидаемая доходность при наименьшем или допустимом уровне риска.

Исходя из преследуемых управляющим целей и его отношения к риску, принято классифицировать инвестиционные портфели следующим образом:

• Агрессивные портфели, нацелены на получение наибольшего инвестиционного дохода от операций с ценными бумагами, характеризующимися высоким уровнем ожидаемого риска. В качестве примера можно привести ОПИФ «Газпромбанк – Акции».
• Умеренные портфели, характеризуются среднерыночными значениями ожидаемого риска и ожидаемой доходности. В качестве примера можно привести ОПИФ «Газпромбанк – Сбалансированный».
• Консервативные портфели, отличаются высоким уровнем надёжности инвестиционных вложений. В качестве примера можно привести ОПИФ «Газпромбанк – Казначейский».

Управление инвестиционным портфелем.

Управление инвестиционным портфелем представляет собой совокупность методов и технологических возможностей, применяемых к различным ценным бумагам, и направленных на сохранение первоначальных стоимости инвестиционных вложений, достижение максимального уровня дохода при наименьшем уровне риска и обеспечение общей инвестиционной направленности портфеля.

Управление портфелем инвестиций может быть представлено в качестве активной или пассивной моделей, применяемых исходя из определённой инвестиционной направленности портфеля.

Активная модель управления инвестиционным портфелем предполагает постоянную систематическую работу инвестиционных менеджеров, направленную на повышение эффективности инвестиционной деятельности, путём подбора ценных бумаг с наибольшими ожидаемыми доходностями при допустимом уровне риска. Точное выявление и своевременная покупка недооценённых рынком ценных бумаг, позволяют получить гораздо более высокие результаты, по сравнению с пассивной моделью.

Пассивная модель управления инвестиционным портфелем заключается в формировании хорошо диверсифицированного рыночного портфеля, с заранее фиксированным уровнем риска, рассчитанным на длительный период времени. Данная модель управления является наиболее привлекательной на развитых фондовых рынках с относительно стабильной конъюнктурой в условиях умеренного экономического роста.

Наиболее распространёнными стратегиями управления портфелем ценных бумаг пассивной модели являются:

1) Стратегия копирования индекса – заключается в формировании портфеля, состав, структура и характеристики которого максимально схожи с составом, структурой и характеристиками выбранного фондового индекса. Основной задачей данной стратегии является минимизация стандартного отклонения разности между доходностями сформированного портфеля и копируемого индекса.
Использование стратегии копирования фондового индекса сопряжённо с высокими транзакционными издержками, возникающими в процессе формирования портфеля и связанными с приобретением большого количества содержащихся в выбранном индексе ценных бумаг. Управляющие, с целью минимизации вышеуказанных издержек прибегают к частичному копированию индекса, путём вложений в ценные бумаги, динамика которых наиболее схожа с динамикой фондового индекса.

2) Стратегия скольжения по кривой доходности – представляет собой краткосрочные вложения в долгосрочные долговые ценные бумаги (облигации), характеризующиеся наибольшей годовой доходностью по сравнению с их краткосрочными аналогами. Данная стратегия применяется управляющими с ограниченными инвестиционными горизонтами, предполагающими сохранение восходящей формы кривой доходности в будущем.

3)Стратегия иммунизации инвестиционного портфеля – заключается в выборе долговых ценных бумаг (облигаций) с таким инвестиционным горизонтом, в течение которого на финансовом рынке прогнозируется стабильная процентная ставка, не приводящая к изменению стоимости подобранных ценных бумаг. Так же, в процессе управления сформированным портфелем происходит реинвестирование купонных доходов, позволяющее застраховать портфель от изменения стоимости содержащихся в нём облигаций, вызванного незначительным изменением процентной ставки.

Традиционные механические схемы управления портфелем ценных бумаг имеют следующие основные разновидности:

1) Схема дополнительной фиксированной суммы – характеризуется фиксированной суммой вложений в ценные бумаги через фиксированные временные интервалы. Цикличность колебаний курсов ценных бумаг позволяет получать прибыль за счёт прироста их курсовой стоимости. Реализуется путём приобретения наибольшего количества ценных бумаг при значительном понижении их котировок, и наименьшего количества при повышении соответственно.
Данная схема управления является крайне пассивной и наиболее рискованной в периоды экономической нестабильности, подразумевая усреднение позиций в ценных бумагах с отрицательной доходностью, что приводит к потере значительной стоимости портфеля при наступлении экономического кризиса.

2) Схема фиксированной спекулятивной суммы – подразумевает разделение портфеля ценных бумаг на консервативную и спекулятивную части. Величина спекулятивной части формируется из высокорискованных ценных бумаг и поддерживается на изначально установленном уровне.

3) Схема фиксированной пропорции – так же, как и схема фиксированной спекулятивной суммы подразумевает разделение портфеля на две части, первая из которых должна находиться в заданной пропорции по отношению ко второй.

4) Схема плавающих пропорций – заключается в формировании портфеля ценных бумаг с рядом установленных взаимосвязанных соотношений между спекулятивной и консервативной частью.

Материал из главы моей дипломной работы, пользуйтесь на здоровье.
Продолжение следует, удачной торговли!

Источник