Какую ставку должен назначить банк чтобы при годовой инфляции 12 реальная доходность оказалась 6

Основы актуарной математики

Расчет размера годовой инфляции. Наращение простых процентов с переменной ставкой. Определение выкупной стоимости векселя. Размеры ежегодных выплат при возвращении займа. Процентная ставка погасительного фонда. Цена аренды при годовой ставке процента.

Рубрика	Банковское, биржевое дело и страхование
Вид	практическая работа
Язык	русский
Дата добавления	24.03.2015
Размер файла	22,3 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Практическая работа №1

по дисциплине «Основы актуарной математики»

1. При какой ставки сложных процентов за 1,5 года сумма удваивается?

Прологарифмируем полученное выражение:

Ответ: За 1,5 года сумма увеличится на 0,58%

В день рождения внука бабушка положила в банк $1000 под 4 % годовых. Какой будет эта сумма к семнадцатилетие внука?

где S0 — первоначальная сумма вклада y.e.

P — годовой процент

При сложных процентах:

Ответ: При простых процентах к семнадцатилетию внука сумма буден равна 1680 y.e., а при сложных процентах 17680 y.e.

2. Как найти инфляцию за квартал, если известна годовая инфляция?

Пусть a инфляция за год, тогда инфляция за квартал x находится из уравнения

(1+х)4 = 1+а => 1+х = => x = — 1

Ответ: инфляция за квартал x = — 1

3. Какую ставку должен назначить банк, чтобы при годовой инфляции 12% реальная ставка оказалась 6%?

По формуле требуемая номинальная ставка равна:

Для получения приближенного решения можно воспользоваться оценкой и прийти к достаточно точному значению.

Ответ: банк должен назначить ставку 18%, чтобы при годовой инфляции 12% реальная ставка оказалась 6%.

4. Наращение простых процентов с переменной ставкой. Пусть простые проценты за k-й год равны . Найдите наращенную сумму через n лет.

S = P*(1+n1i1+ n2i2 + …… + nkik) = P*(1+ ),

где P — первоначальная сумма

it — ставка простых процентов в периоде с номером t, t = 1,k

nt — продолжительность t периода начисления по ставке it, i = 1, k.

5. Наращение сложных процентов с переменной ставкой. Пусть сложные проценты за k-й год равны . Найдите наращенную сумму через n лет.

S = P* (1+i1)n1 * (1+i2)n2 ……*(1+im)nm = P*nk,

где i1, i2, i3, ….. im — значения ставок процентов, действующих в соответствующие периоды n1, n2, n3,……. nk времени.

6. По договору зафиксирован платеж через 3 года в размере 1000 д.е. Через год процентная ставка увеличилась. Кому это выгодно: тому, кому будут платить, или тому, кто будет платить?

7. Найдите пять сумм в прошлом и в будущем, эквивалентных сумме 10 000 грн. в момент времени 0, при ставке процента 20,5%.

S5= (1+0,205)5-0*10 000 = 25 405 грн.

S4= (1+0,205)4-0*10 000 = 21 083 грн.

S3= (1+0,205)3-0*10 000 = 17 496 грн.

S2= (1+0,205)2-0*10 000 = 14 520 грн.

S1= (1+0,205)1-0*10 000 = 12 050 грн.

S-0= (1+0,205)0-0*10 000 = 10 000 грн.

S-1= (1+0,205)-1-0*10 000 = 8298 грн.

S-2= (1+0,205)-2-0*10 000 = 6886 грн.

S-3= (1+0,205)-3-0*10 000 = 5715 грн.

S-4= (1+0,205)-4-0*10 000 = 4742 грн.

S-5= (1+0,205)-5-0*10 000 = 3936 грн.

Ответ: 25405, 21 083, 17 496, 14 520, 12 050, 10 000, 8298, 6886, 5715, 4742, 3936 грн.

8. Вексель номиналом 10 000 учтен банком за 12с+40 дней срока погашения. Определить выкупную стоимость векселя, если учетная ставка равна 26% годовых

Дан номинал векселя Р = 10000, количество дней до срока погашения t = 76, учетная ставка i = 26% = 0,26.

S = P * (1 — i/360*t), где 360 — это временная годовая база.

S = 10000 * (1 — 0,26 / 360 * 76) = 9450 д. е.

Ответ: сумма полученная владельцем векселя 9450д. е.

9. Покупатель предложил два варианта расчетов при покупке дачи: 1) $5000 немедленно и затем по $1000 в течение 5 лет; 2) $8000 немедленно и по $300 в течение 5 лет. Какой вариант выгоднее для продавца при годовой ставке процента: а) 10,5% , б) 5%.

1000*(1+0,105)5 = 1647,44 + 5000 = 6 647,44$ — выгоднее

1000*(1+0,05)5 = 1276,28 + 5000 = 6 276, 28$

300*(1+0,05)5 = 382,88 + 800 = 8 382, 88$

300*(1+0,105)5 = 494,23 + 8000 = 8 494, 23$ — выгоднее

Ответ: при выплате 5000$ немедленно и затем 1000$ в течении 5 лет, при ставке 10,5% выгоднее и при выплате 8000$ немедленно и затем 300$ в течении 5 лет, при ставке 10,5% выгоднее.

10. Бизнесмен арендовал виллу за $10 000 в год. Какова выкупная цена аренды при годовой ставке процента 2.25% Решение. Эта выкупная цена есть современная величина всех будущих арендных платежей и равна

Это в точности годовые процентные деньги, которые стал бы получать арендодатель с 444444,4, помещенных в банк под упомянутую процентную ставку.

11. Заем величиной 12000 грн. был взят под 10,5% годовых на 6 лет. Найти размеры ежегодных выплат при возвращении займа следующими способами:

-погашение долга одним платежом в конце срока;

По таблице мультиплицирующих множителей M(6;10,5) = 1,772 Значит искомый платеж равен:

R = 12 000*1,772 = 212,64 грн.

-погашение основного долга одним платежом в конце:

R = iD + D = 0,105 * 12 000 + 12 000 = 13260 грн.

-погашение основного долга равными годовыми выплатами:

R1 = D/n + + 0.105*12000 = 2000 + 1260 = 3260 грн.

R2 = D/n + i(D-D/n) = 12000/6 + 0.105*10000 = 2000 + 1050 = 3050 грн.

R3 = D/n + i(D-2D/n) = 12000/6 + 0.105*8000 = 2000 + 840 = 2840 грн.

R4 = D/n + i(D-3D/n) = 12000/6 + 0.105*6000 = 2000 + 630 = 2630 грн.

R5 = D/n + i(D-4D/n) = 12000/6 + 0.105*4000 = 2000 + 420 = 2420 грн.

R6 = D/n + i(D-5D/n) = 12000/6 + 0.105*2000 = 2000 + 210 = 2210 грн.

-погашение займа равными годовыми выплатами;

Из таблицы коэффициентов приведения ренты находим а(6;10,5) = 4,35526

Значит R = 12 000/4,35526 = 2755,289 грн.

-погашение потребительского кредита равными ежемесячными выплатами;

R = D*(1+ni)/nm = 12000 * (1 + 6 * 0,105) / 6*12 = 39120грн.

-формированием погасительного фонда по более (вдвое) высоким процентам и погашением долга одним платежом в конце:

Процентная ставка погасительного фонда в 2 раза больше, следовательно

Размер фонда должен составлять

S = D = (1+i)n = 12000*(1+0,105)6 = 12000*1,820 = 21840 грн.

Фонд представляет собой ренту, тогда S будет наращенная величина ренты. Из формулы наращенной величины найдем ежегодный платеж.

s(6,34) = ((1+0,34)6 — 1) / 0,34 = 14.086 R = 21840 / 14.086 = 1550,47 грн.

12.Задан инвестиционный проект: Inv = 40000 д.е., последующий годовой доход при 9% годовых равен R=10000, длительность проекта 7 лет. Найти характеристики инвестиционного проекта, то есть NPV, NFV, срок окупаемости (если проект окупается) и IRR.

Решение: Поток доходов есть конечная годовая рента с годовым платежом R, длительностью n лет. Современная величина этой ренты

где а(7;9) = 5,0329528. Значит приведенный чистый доход проекта есть

NPV = Inv + R* а(7,9) = — 40 000 + 10 000 * 5,0329528= 10329,528 грн.

d = NPV/ Inv = 10329,528/40 000 = 0,25 = 25%

Для нахождения внутренней доходности найдем такое g, что а (7,g) = 40 000/10 000 = 4; a(7,25) = 3,1611392 => g = 31%.

NFV = NPV*(1+i)tn = 10329,528 *(1+0,9)7 = 923327,315 грн.

Внутренняя норма доходности авансированного в проект капитала IRR = (10329,528/40 000)*100 = 25%.

13.Оборудование стоимостью 10000 д.е. арендуется сроком на 5 лет. Срок амортизации оборудования 8 лет. Рассчитайте ежегодный арендный платеж, если ставка равна 11% годовых.

Решение: Остаточная стоимость оборудования равна

S = P(1-nh) =>10 000*(1-5*0,08) = 6 000 д.е.

Следовательно годовой платеж

инфляция процент вексель заем

R = (P — S/(1+j)n) / a(n,j) = (10 000 — 6000/(1 + 0,11)5)/2,8034730 = 6439/2,8034730 = 2296,7940 д.е.

Ответ: ежегодный арендный платеж 2296,7940 д.е.

Размещено на Allbest.ru

Подобные документы

Особенности расчета процентной ставки при сложном и простом проценте. Сроки выплаты кредита, взятого под простую ставку. Определение величины взноса при начислении процентов ежеквартально по ставке сложных процентов годовых для накопления заданной суммы.

контрольная работа [23,8 K], добавлен 29.10.2012

Расчет реальной процентной ставки по депозиту на основе имеющейся информации. Целесообразность размещения средств на депозит. Определение дохода и годовой доходности для продавца векселя и банка. Анализ нехватки или избытка денежных средств в экономике.

контрольная работа [42,0 K], добавлен 21.06.2010

Формула для определения простой ставки процентов по кредиту, компенсирующей ожидаемую инфляцию. Расчет ставки, которую использовал банк при учете векселя. Задача на определение суммы, которую получит владелец депозита, по окончанию срока договора.

контрольная работа [22,4 K], добавлен 19.04.2011

Определение уровня процентной ставки при осуществлении финансовых операций, размера долга для различных вариантов начисления процентов по кредитам. Расчет суммы, полученной владельцем векселя и величины дисконта, эквивалентной годовой учетной ставки.

контрольная работа [24,8 K], добавлен 15.10.2010

Срок удвоения капитала при начислении сложных процентов раз в год по процентной ставке. Схема начисления сложных процентов, сравнение эффективной и номинальной ставок. Определение ставки по кредиту с целью получения дохода с учетом темпа инфляции.

курсовая работа [465,6 K], добавлен 26.09.2011

Решение задачи на нахождение дохода вкладчика по заданной процентной ставке по вкладу, расчет приводится по Английской практике. Определение страхового процента и дохода по факторинговой операции. Составление графика выплаты лизинговых платежей.

задача [369,3 K], добавлен 12.05.2011

Процентная ставка как плата за кредит. Подходы по начислению и учету процентов по кредиту в банках. Методы начисления процента по размещенным и привлеченным средствам банка. Бухгалтерский учет операций по начислению и получению банком процентов.

курсовая работа [38,6 K], добавлен 14.06.2015

Источник

Лабораторная работа: Наращение и дисконтирование. Потоки платежей. Ренты

Факультет дистанционного обучения

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Лабораторная работа № 1

по дисциплине «Математическая экономика»

выполнена по учебному пособию А.А.Мицель «Математическая экономика»

Новицкий Александр Витальевич

Лабораторная работа №1. Наращение и дисконтирование. Потоки платежей. Ренты.

Вопрос 1. Современная величина обычной ренты

Современная величина ренты является важнейшей характеристикой потока платежей, которая определяет стоимость будущего денежного потока на настоящий момент времени. Эта характеристика служит осно­вой для многих методов финансового анализа. По определению, совре­менная величина – это сумма всех дисконтированных членов потока платежей на начальный или предшествующий ему момент времени. Ино­гда вместо термина современная величина используют термины приве­денная или капитализированная сумма платежей. При определении со­временной величины потока платежей важно правильно установить период времени от начала потока (момента времени, на который произ­водится оценка) до момента поступления платежа (в годах). После этого можно применять формулы дисконтирования.

.

коэффициент приведения ренты равен

Вопрос 2. Принцип финансовой эквивалентности обязательств.

Этот принцип гарантирует безубыточность изменений финансовых отношений для каждой из сторон. Эквивалентными считаются платежи, которые, будучи приведёнными по заданной процентной ставке к одному моменту времени, оказываются равными.

Вопрос 3. Каким образом учитывается инфляция при вычислении наращенной суммы?

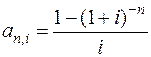
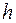Существует множество различных способов учета инфляции при на­ращении сложных процентов. Рассмотрим один из них, основанный на применении формулы Фишера. Пусть – ожидаемый годовой темп инфляции в виде ставки сложных процентов (мы не касаемся здесь методики определения этого показателя), 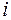– ставка процентов без учета инфляции, 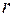– реальная ставка с учетом инфляции. Тогда реальная ставка определяется из урав­нения, которое называется уравнением Фишера:

.

Решая это уравнение относительно , получим

.

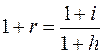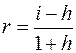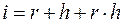Ставка без учета инфляции (которую называют также номинальной ставкой) . При малых значениях 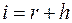используют приближен­ную формулу , а для реальной ставки: .

Вопрос 4. Как определяется эффективная ставка?

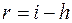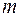Для сравнения различных условий начисления процентов (при различных номинальных ставках и различном количестве начислений) используют понятие эффективной ставки. Эффективная ставка – это годовая ставка процентов, начисляемых один раз в год, которая дает тот же финансовый результат, что и — разовое начисление в год с использованием номинальной ставки 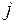. Таким образом, по определению, должно выполнятся равенство множителей наращения

,

где – эффективная ставка. Отсюда получаем

.

Задача 1. Какую ставку должен назначить банк, чтобы при годовой инфляции 12% реальная ставка оказалась равной 6%?

Пусть – ожидаемый годовой темп инфляции в виде ставки сложных процентов (мы не касаемся здесь методики определения этого показателя), – ставка процентов без учета инфляции, – реальная ставка с учетом инфляции. Тогда реальная ставка определяется из урав­нения, которое называется уравнением Фишера:

.

Решая это уравнение относительно , получим

Задача 2. Вы заключили депозитный контракт на сумму 90 000 на 4 года при 11% ставке. Если проценты начисляются ежегодно, какую сумму Вы получите по окончании контракта?

наращенная сумма – это первоначальная сумма с начисленными на эту сумму процентами. Введем следующие обозначения. Пусть

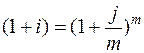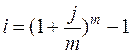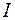– сумма процентов за весь срок;

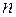– общее количество периодов начисления (обычно в годах);

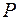– первоначальная сумма;

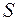– наращенная сумма;

– ставка процентов в виде десятичной дроби.

.

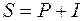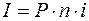При начислении простых процентов за базу принимается первоначальная сумма. Проценты начисляются раз, поэтому и формула простых процентов запишется в виде

.

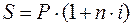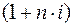Величина называется множителем наращения по простым процентам.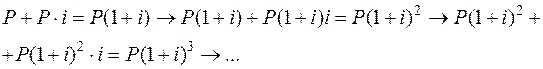

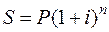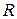Задача 3. По сле внедрения мероприятия по снижению административных издержек предприятие планирует получить экономию 30 000 в год. Сэкономленные деньги предполагается размещать на депозитный счет (под 11% годовых) с тем, чтобы через 5 лет накопленные деньги использовать для инвестирования. Какая сумма окажется на банковском счету предприятия?

В долгосрочных финансовых операциях для наращения первоначальной суммы применяют сложные проценты. При начислении сложных процентов за базу принимают не первоначальную сумму, а сумму, получившуюся после начисления процентов и присоединения их к сумме долга в предыдущих периодах.

Присоединение начисленных процентов к сумме, которая служила базой для их начисления, называют капитализацией процентов. Процесс капитализации происходит по следующей схеме:

В общем виде формула наращения по сложным процентам запишется так:

.

S=30000(1+0,11) 5 =50551,74465

Задача 4. Провести детальный анализ ренты длительностью 4 года, годовым платежом = 90 000 . и переменной процентной ставкой: 5% во 2-м году, 8% — в 3-м, 10% — в 4-м году. Определить современную величину этой ренты?

Сначала определим приведенную величину платежей первого промежутка на начальный момент:

.

i1=0% (по условию за 1-й год)

Приведённая величина платежей второго промежутка на его начало (то есть на момент ):

.

Эта же величина, приведенная на начало всего срока (на нулевой момент):

*v₁ n1

следовательно A₂ =85714,28571

Вычисляем приведённая величину платежей третьего, четвертого промежутка

приведённая величина платежей третьего промежутка

приведённая величина платежей четвертого промежутка

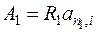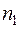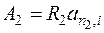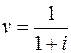
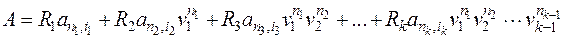
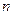Задача 5. Вычислить — годичную ссуду покупки квартиры за A рублей с годовой ставкой 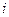процентов и начальным взносом 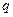процентов. Сделать расчет для ежемесячных и ежегодных выплат. =

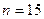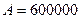Расчет провести для следующих данных: ; руб.;

Если задана современная величина ренты, то

.

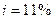
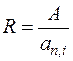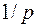Интервал между платежами у ренты равен , размер платежа .

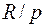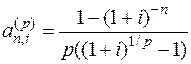Обозначим – коэффициент приведения 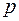-срочной ренты.

a_n=15,i=0,11 =(1-(1+0,11) 15 )/(12((1+0,11) 0,0833 -1))=7,546579303

Источник

Название: Наращение и дисконтирование. Потоки платежей. Ренты Раздел: Рефераты по математике Тип: лабораторная работа Добавлен 21:00:34 23 июля 2011 Похожие работы Просмотров: 445 Комментариев: 14 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать