Как рассчитать среднюю доходность за 3 года

Курс лекций «Основы финансового менеджмента»

5.2. Определение средней доходности

В практике финансовых расчетов часто возникает необходимость расчета средней доходности набора (портфеля) инвестиций за определенный период или средней доходности вложения капитала за несколько периодов времени (например, 3 квартала или 5 лет). В первом случае используется формула среднеарифметической взвешенной , в которой в качестве весов используются суммы инвестиций каждого вида. Вернемся к примеру из предыдущего параграфа с вложением 1000 рублей в два вида деятельности: торговую и финансовую. Можно сказать, что владелец этих денег сформировал инвестиционный портфель, состоящий из двух инструментов – инвестиции в собственный капитал магазина и финансовые (спекулятивные) инвестиции. Сумма каждого из вложений составила 500 рублей. Доходность по первому направлению вложений составила 10%, по второму – 40% годовых. Применив формулу средней арифметической (в данном случае, ввиду равенства весов, можно использовать среднюю арифметическую простую) получим среднюю доходность инвестиций за год, равную 25% ((10 + 40) / 2). Она в точности соответствует полной доходности “портфеля”, рассчитанной в предыдущем параграфе. Если бы владелец изменил структуру своих инвестиций и вложил в торговлю только 300 рублей (30%), а в финансовые спекуляции 700 рублей (70%), то при неизменных уровнях доходности каждого из направлений средняя доходность его “портфеля” составила бы 31% (10 * 0,3 + 40 * 0,7). Следовательно, общую формулу расчета средней доходности инвестиционного портфеля можно представить следующим образом:

, где (5.2.1)

n – число видов финансовых инструментов в портфеле;

r i – доходность i -го инструмента;

w i – доля (удельный вес) стоимости i -го инструмента в общей стоимости портфеля на начало периода.

Реальный срок вложения капитала может принимать любые значения – от одного дня до многих лет. Для обеспечения сопоставимости показателей доходности по инвестициям различной продолжительности эти показатели приводятся к единой временной базе – году (аннуилизируются). Методика аннуилизации доходности была рассмотрена в предыдущем параграфе. Однако, годовая доходность одних и тех же инвестиций может быть неодинаковой в различные промежутки времени. Например, доходность владения финансовым инструментом (за счет прироста его рыночной цены) составила за год 12%. В течение второго года цена увеличилась еще на 15%, а в течение третьего – на 10%. Возникает вопрос: чему равна средняя годовая доходность владения инструментом за 3 года? Так как годовая доходность суть процентная ставка, средняя доходность за период рассчитывается по формулам средних процентных ставок. В зависимости от вида процентной ставки (простая или сложная) ее средняя величина может определяться как среднеарифметическая, взвешенная по длительности периодов, в течение которых она оставалась неизменной, или как среднегеометрическая , взвешенная таким же образом (см. § 2.2).

В принципе возможно применение обоих способов для определения средней за несколько периодов доходности. Например, среднеарифметическая доходность инструмента, о котором говорилось выше, составит за три года 12,33% ((12 + 15 + 10) / 3). В данном случае продолжительность периодов, в течение которых доходность оставалась неизменной (год), не менялась, поэтому используется формула простой средней. Применив формулу средней геометрической, получим r ср = 12,315% (((1 + 0,12) * (1 + 0,15) * (1 + 0,1)) 1/3 -1). При незначительной разнице в результатах, техника вычисления среднеарифметической доходности значительно проще, чем среднегеометрической, поэтому довольно часто используется более простой способ расчета.

Однако при этом допускается существенная методическая ошибка : игнорируется цепной характер изменения доходности от периода к периоду. Доходность 12% была рассчитана к объему инвестиций на начало первого года, а доходность 15% — к их величине на начало следующего года. Эти величины не равны друг другу, так как в течение первого года инвестиции подорожали на 12%. За второй год они стали дороже еще на 15%, то есть их объем на начало третьего года также отличался от двух предыдущих сумм. Применяя формулу средней арифметической, молчаливо предполагают, что объем инвестиций оставался неизменным в течение всех периодов, то есть по сути рассчитывается средний базисный темп прироста. В данном случае это предположение совершенно неверно, поэтому следует рассчитывать средний цепной темп прироста по формуле средней геометрической, так как начальная сумма инвестиций меняется от периода к периоду. Представим исходные данные примера в табличной форме (табл. 5.2.1).

Таблица 5.2.1
Динамика доходности акции за 3 года
руб.

Источник

Правильный расчет среднегодовой доходности в инвестициях

Любой инвестор рано или поздно должен подвести итоги и рассчитать доходность инвестиций. Так как цифры вроде 125% за 5 лет мало информативны, то доходность принято приводить доходность к годовым значениям. Такую доходность называют среднегодовой доходностью. В случае с 125% за 5 лет среднегодовая доходность равна 17,6%. 125% принято назвать накопленной доходностью.

Как рассчитать среднегодовую доходность

Если период инвестиций измеряется в годах, то формула среднегодовой доходности выглядит следующим образом:

R – накопленная доходность
r – среднегодовая доходность
T– срок инвестиций (в годах)

Эта формула предполагает капитализацию процентов. Её нельзя применять, например, в тех случаях, когда дивиденды выводились из инвестиций (не реинвестировались).

В случае произвольного промежутка инвестиций среднегодовая доходность считается по аналогии.

R – накопленная доходность
r – среднегодовая доходность
T– срок инвестиций (в месяцах)

Здесь период инвестиций измеряется в месяцах. Если необходимо рассчитать с точностью до дней, то 12 надо заменить на 365.

Пример вычисления:

Инвестор получил доходность 12% за 16 месяцев. Чему равна его годовая доходность?

Основные ошибки при вычислениях

Чаще всего начинающие инвесторы допускают ошибку, считая следующим образом (пример с доходностью 125% за 5 лет):

Или в примере с 12% за 16 месяцев:

Такой вариант расчетов в инвестициях использовать нельзя, так как при этом не учитывается капитализация процентов.

Источник

Как посчитать реальную среднегодовую доходность ваших инвестиций?

Есть два способа подсчета доходности инвестиций: ср. арифметический и ср. геометрический. Первый способ показывает завышенные результаты. Чем сильнее колеблется цена актива по годам, тем сильнее будут отличаться эти доходности.

Зачастую управляющие показывают только ср. арифметическую доходность, чтобы завлечь инвесторов. Последние «покупаются», вкладываются, а затем их доходность оказывается гораздо ниже, чем они ожидали, судя по рекламе.

Пример. Фонд в первый год получил + 100%, во второй -50% доходности. Ср. арифм. доходность равна (100-50)/2= 25%. А ср. геом. доходность равна (1+100/100)*(1-50/100)-1 = 2*0,5-1= 0. То есть управляющий вам говорит в рекламе: «Наша средняя доходность 25%». А в реальности, если бы вы вложили на два года деньги, то получили бы 0% доходности.

Можно проверить это «на пальцах»:

• вкладываете 100 руб. С учетом доходности 100%, на счете 200 руб. в конце года;
• на второй год -50%. Т.е. 200 руб. — 100 руб. = 100 руб. Заработали 0.

Для того, чтобы не обмануться при подсчете доходности и не «повестись» на недобросовестную рекламу, нужно рассчитывать ср. геометрическую доходность.

Шаг. 1.Поделите конечную стоимость актива на начальную, или конечную доходность на начальную

Шаг 2. Получившееся число подставьте в он-лайн калькулятор корней

Шаг 3. В качестве корня задайте количество лет

Шаг 4. Вычтите 1 (единицу)

Пример. Страховая компания гарантируют вам 140% доходности за 15 лет инвестиций в структурный продукт (индекс S&P 500). Какова же ср. годовая гарантированная доходность ваших инвестиций?

Ответ: Исчисляем ср. геометрическую доходность. Делим 140/100 = 1,4. Подставляем 1,4 в калькулятор корней, в качестве корня указываем количество лет — 15. Получаем число 1,0227. Вычитаем 1(единицу), получаем 0,0227, что в переводе в % будет означать 2,27% в год.

Если у вас есть данные о доходности по каждому году, а вам нужно посчитать ср. геом. доходность за весь период, формула будет более сложной.Лучше посчитать в Excel.

Ср. геом. доходность по годам =СТЕПЕНЬ (((1+R1)*(1+R2)..*(1+Rn));1/N)-1

где R — доходность в году в формате десятых и сотых (например, вместо 25% нужно писать 0,25), n — кол-во лет.

Как посчитать разницу между ср. арифм. и ср. геом. доходностью

Это нужно для тех, кто строит прогнозы на будущее. Примерно эти доходности отличаются на величину = 0,5 * (стандартное отклонение цены актива)² .Стандартное отклонение берется в формате десятых и сотых (например, 0,25).

Стандартное отклонение — это и есть риск актива. Иными словами риск актива — это до каких пределов в среднем может колебаться цена актива. Например, от +25% до — 25%. Акции более рискованны, чем облигации, потому что их цена может колебаться в + или в — на больший %.

Источник

Цифры, числа и проценты — как правильно считать прибыль и годовую доходность | Несколько простых способов с интересными примерами

Проходили в школу простые и сложные проценты? Ну как вам? Скукотища. Какие-то цифры, числа. Математические действия: умножение, деление, вычитание и сложение. Но все меняется, когда речь идет о деньгах. Собственных деньгах. Потенциале их роста от инвестиций. Сразу происходит смена настроения абсолютно на противоположное. От просто скучно до интересно.

И самыми любимыми становятся сложение и умножение. Складывать (суммировать) капитал и приумножать (зарабатывать) прибыль.

Расскажу про пару способов и приемов, как можно достаточно просто и быстро оценивать и считать результаты вложений (будущие и реальные). И главное, правильно.

Есть еще люди «в наших селеньях», кто не знает (или просто забыл) как все это делается.

Нам нужен калькулятор и один палец (не показывать, а нажимать на кнопки). В некоторых случаях просто мозги.

Складываем годовые доходности

Вы получили в первый год прибыль в 10%, во второй снова 10%. А на третий год? . опять десять.

Внимание вопрос. Сколько вы заработали за 3 года?

Быстрый ответ — 30% прибыли.

Мы посчитали 30% по правилам простых процентов. Просто сложив их вместе.

Если срок короткий и (или) доходность небольшая (не 20-30 и тем более не 50-100%), то результат будет близок к истине. Но как вы поняли, неправильный.

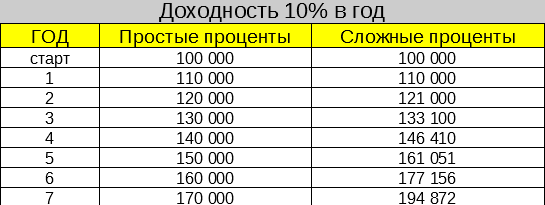
Представьте, что в течение 7 лет вы получаете по 10% годовых на вложенный капитал. Пусть будет на 100 тысяч.

Сколько мы заработаем за этот срок?

Снова быстрый ответ: 70% прибыли или 70 тысяч.

На самом деле — 95 тысяч рублей. Вы только что потеряли (недосчитали) 25 000.

Доходности нужно не складывать, а умножать между собой.

10% со 100 рублей, дадут 10. В совокупности будет 110.

Во второй год 10% берем со 110 — 11. Получаем в итоге — 121 рубль.

Третий год — принесет нам 12,1. Итого — 133,1 рубль.

Как это все подсчитать?

Проценты преобразуем по формуле: 1+ (доходность за год/100%). И перемножаем.

Соответственно 20% — это будет 1.2; 30% -1.3; 45% — 1.45.

В нашем случае: 1,1 х 1,1 х 1,1 и так далее. семь раз.

Правила расчета простых и сложных процентов

Прибыль + убытки — как сложить?

Как сложить между собой прибыльные и убыточные периоды?

Простой вопрос. В первый год получили прибыль +10% . За второй убыток -10% . Сколько денег будет в итоге?

Вроде бы плюс на минус дает ноль. Десять туда, 10% обратно.

Мы в той же точке отсчета.

На самом деле мы потеряли 1% (можете проверить на калькуляторе).

Причем последовательность не важна. Получена сначала прибыль, потом убыток. Или наоборот. Результат будет один.

Как быстро подсчитать?

• 10 процентов прибыли — 1,1;
• 10% убытка — 0,9.

Формула: 1- (убыток за период/100).

Перемножаем числа между собой и получаем результат.

В нашем случае: 1.1 Х 0.9 = 0,99. Или 99% от первоначального капитала.

Методы 72

Метод семидесяти двух позволяет быстро узнать, через сколько лет ваши вложения удвоятся.

Для этого нужно число 72 разделить на ожидаемую годовую доходность.

Например, при ежегодной прибыли в 7% — вы удвоите капитал примерно через 10 лет.

Увеличиваем доходность до 14,4% — и каждые 5 лет получаем прибыль 100%.

Через 10 лет у вас будет в четыре раза больше денег, через 15 — в 8 раз, через 20 — в 16.

Ну а «потерпев» 30 лет — вы увеличите свой капитал в 64 раза.

Метод 72 не блещет математической точностью. Всегда есть небольшая погрешность. Но на лету быстро посчитать и получить приблизительный результат — самое оно.

Кстати формула работает и в обратном направлении.

Ежегодный убыток в 6%, примерно через 12 лет ополовинит ваш капитал.

Интересно это использовать при инфляции. Насколько уменьшается покупательная способность денег.

Средняя инфляции в РФ за последние десять лет составила 7,43%.

Это значит, что рубль «усох» в 2 раза за 9,5 лет.

Метод 114

Все аналогично способу подсчета 72 (делим 114 на годовой доход). Но формула показывает утроение капитала за период. Тоже с небольшой погрешностью.

Пара примеров утроения капитала.

При доходности в год:

• 8% | (114 / 8) = 14,2 года
• 10% | (114 / 10) = 11,4 года
• 12% | (114 / 12) = 9,5 лет
• 14% | (114 / 14) = 8,1 год.

Среднегодовая прибыль за несколько лет

Как посчитать среднегодовую прибыль за различные периоды? А зачем?

Начнем с примера. Дальше поймете, нужна вам эта инфа или нет.

Два инвестора Вася и Петя начинаются мериться своими достоинствами доходностями. У кого больше. И кто круче.

Вася: Я раскачал свои 250 тысяч за 5 лет до 580 кусков. Заработал 330 000 рублей прибыли.

Петя: Мои скромные 40 тысяч я превратил в сотку всего за 6 лет. Прибыль 60 тысяч.

А кто из них действительно в большем плюсе от суммы вложенного капитала. У кого прибыль в процентах выше?

Вася за 5 лет получил 132% прибыли.

Петя заработал 150%, но за 6 лет.

Можно выделить среднегодовую доходность и увидеть, кто зарабатывал в год больше. Делим общий процент прибыли на количество лет.

Вроде бы Вася круче. У него больше. Хоть и ненамного.)))

Но мы немного неправильно вычленили годовую доходность.

Среднегодовая доходность = n√(Pn/P0)-1; где

• n — количество периодов (лет);
• P0 — начальное значение капитала;
• Pn — конечное размер

УУУУ. Какие-то корни. И даже не квадратные. И еще не все калькуляторы это поддерживают. Забудьте ее навсегда.

Мне больше нравится считать в электронных таблицах (Excel вам в помощь).

Есть такая формула.

=степень (Pn/P0; 1/n) — 1

Вносим 3 параметра — начальный, конечный капитал и срок вложений.

Получаем:

Рост за 6 лет у Пети с 40 до 100 тысяч соответствует среднегодовой доходности в 16,5%.

Вася, получивший сверху 330 тысяч за 5 лет зарабатывал в среднем по 18,3%.

Обратите внимание, как кардинально поменялись результаты по сравнению с простым делением общей прибыли на количество лет.

И наш «крутыш» Вася хоть и остается в лидерах, но среднегодовая прибыль уменьшилась почти в 1,5 раза..

Где еще можно применять такую формулу?

Для примера несколько вариантов использования.

Биржевые графики

Смотрим на какой нибудь биржевой график (акции, индекс, ETF). Нам нужно примерно оценить как он растет в среднем в год. На сколько процентов?

Например, за последние 5, 10, 20, 30 лет (да хоть сто лет).

Можно конечно поискать информацию в интернете. Есть различные статистические данные. Таблицы. Красивые цифры.

Но мы легкие пути не ищем. Рассчитаем все сами.

Нам нужна бутылка водки (хотя можно и без нее обойтись), начальная и конечная цена за требуемый период.

И электронная таблица. Особенно, если есть какой-то готовый шаблон — дело пары секунд (Спойлер: шаблон есть ниже). Вносим 3 числа и результат моментально перед глазами.

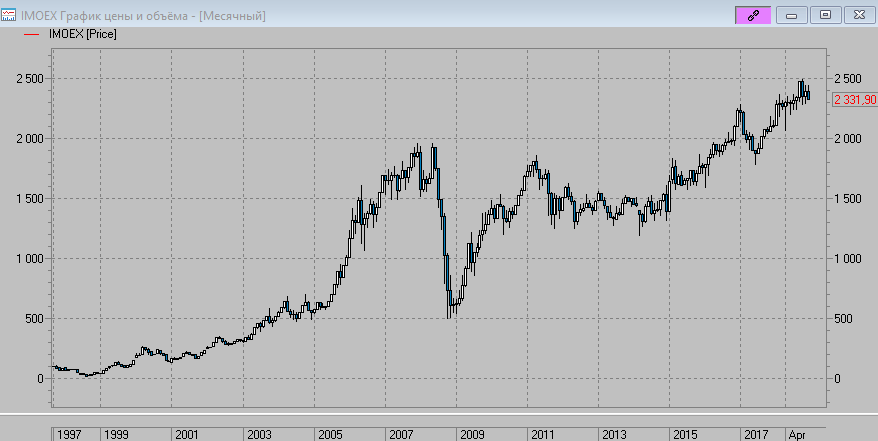
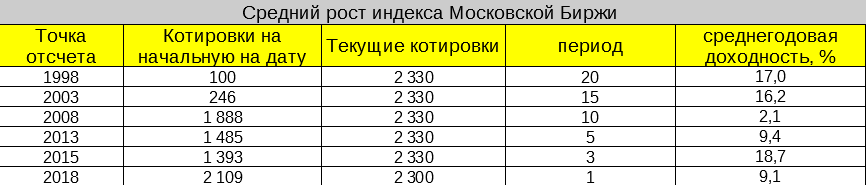
Для примера возьмем наш любимый и родной индекс Московской биржи. С момента его основание и по текущий момент.

Текущий (2018 год) еще правда не закончился (конец декабря). Но это не сильно критично.

В таблице видно на сколько процентов в среднем рос рынок в зависимости от точки входа.

Интересный момент с удорожанием продуктов.

Стоила лет десять назад булка хлеба 10 рублей. А сейчас ее цена 35 рубликов.

Молоко продавали за 20, а сейчас за 60 (данные я взял с потолка, просто для примера).

И так понятно, что грабеж среди бела дня. Но как его подсчитать?

Забиваем данные в таблицу и видим, что хлеб дорожал в среднем на 13,3% в год. А молоко всего на 11,6%.

Чего нам ждать в будущем: выравнивание пропорции цен? Хлеб стоит явно дороже, чем должен. Значит . скоро цены на него снизятся. ))))

А может на молочко еще подрастут (что более вероятно).

Дивиденды

Вернее темпы их роста. Интересная штука, скажу я вам.

Дивидендные аристократы (обычно компании из Америки) из года в год стараются повышать уровень выплат для своих акционеров. В России есть немного таких компаний, действующих подобных образом.

Вот статистика выплат дивидендов за последние несколько лет.

Лукойл — Дивиденды по годам

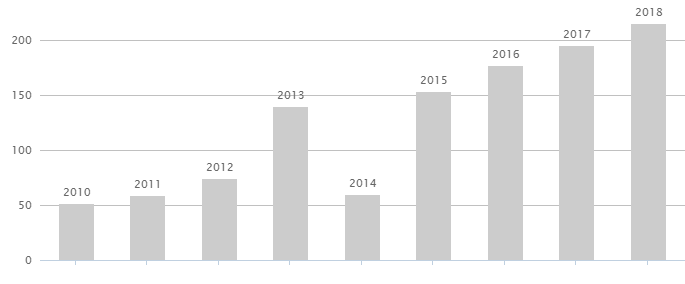
За восемь лет, размер дивидендов вырос со скромных 52 рубля на акцию в 2010, до 215 рублей в 2018 году. Ежу понятно, что это уже неплохо. Но . насколько неплохо?

С помощью формулы, можно определить среднегодовой темп прироста дивидендов.

Получаем 19,4% в год. Рост прибыли только за счет дивидендов. (Котировки на акции Лукойл тоже за это время выросли порядком). Обгоняющий инфляцию минимум в 2 раза.

Ради интереса рассчитал темпы роста дивов по другим голубым фишкам российского рынка: Газпром, Сбербанк и МТС.

Очень любопытная картина получилась.

Среднегодовой рост дивидендов

По старой традиции для ленивых (или тех кто ценит свое время) прикладываю файл со всем, что здесь было написано, описано, рассчитано. Может кому и пригодится. При необходимости переделайте под себя.

Всем удачных (и правильно подсчитанных) положительных доходностей!

За обновлениями в этой и других статьях теперь можно следить на Telegram-канале: @vsedengy.

Источник