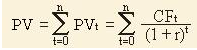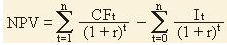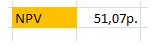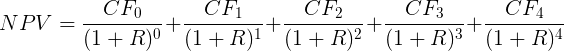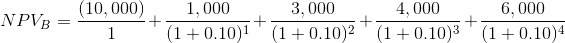Как рассчитать npv для бизнес плана

Анализ инвестиционного проекта. Пример расчета NPV и IRR в Excel

Рассмотрим анализ инвестиционного проекта: рассчитаем основные ключевые показатели эффективности инвестиционного проекта. Среди ключевых показателей можно выделить два наиболее важных – NPV и IRR.

• NPV – чистый дисконтированный доход от инвестиционного проекта (ЧДД).
• IRR – внутренняя норма доходности (ВНД).

Рассмотрим данные показатели более детально и рассчитаем простой пример работы с ними в таблицах Excel.

Чистый дисконтированный доход (NPV )

NPV (Net Present Value, Чистый Дисконтированный Доход) – пожалуй, один из наиболее популярных и распространенных показателей эффективности инвестиционного проекта. Рассчитывается он как разница между денежными поступлениями от проекта во времени и затратами на него с учетом дисконтирования.

Расчет чистого дисконтированного дохода (NPV):

1. Определить текущие затраты на проект (сумма инвестиционных вложений в проект) – Io.
2. Произвести расчет текущей стоимости денежных поступлений от проекта. Для этого доходы за каждый отчетный период приводятся к текущей дате (дисконтируются) – PV.
3. Вычесть из текущей стоимости доходов (PV) наши затраты на проект (Io). Разница между ними будет чистый дисконтированный доход – NPV.

PV что это такое и как рассчитать? Расчет дисконтированного дохода

Расчет чистого дисконтированного дохода (NPV)

NPV=PV-Io

CF – денежный поток от инвестиционного проекта;
Iо – первоначальные инвестиции в проект;
r – ставка дисконта.

Показатель NPV – показывает инвестору доход/убыток от инвестирования денежных средств в инвестиционный проект. Данный доход он может сравнить с доходом в наименее рискованный вид активов – банковский вклад и рассчитать эффективность и целесообразность вложения в инвестиционный проект. Если NPV больше 0, то проект эффективен. После этого можно сравнить значение NPV с доходов от вклада в банк. Если NPV > вклад в наименее рискованный проект, то инвестиции целесообразны.

Формула чистого дисконтированного дохода (NPV) изменяется если инвестиционные вложения в проект осуществляются в несколько этапов (периодов) и имеет следующий вид.

CF – денежный поток;
It – сумма инвестиционных вложений в проект в t-ом периоде;
r – ставка дисконтирования;
n – количество этапов (периодов) инвестирования.

Оценка стоимости бизнеса	Финансовый анализ по МСФО	Финансовый анализ по РСБУ
Расчет NPV, IRR в Excel	Оценка акций и облигаций

Внутренняя норма доходности (IRR). IRR что это за показатель

Внутренняя норма доходности (Internal Rate of Return, IRR) – второй наиболее популярный показатель оценки инвестиционных проектов. Он определяет ставку дисконтирования, при которой инвестиции в проект равны 0 (NPV=0). Другими словами затраты на проект равны доходам от инвестиционного проекта.

IRR = r, при которой NPV = 0, находим из формулы: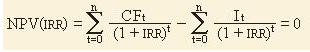

CF – денежный поток;
It – сумма инвестиционных вложений в проект в t-ом периоде;
n – количество периодов.

Расчет IRR позволяет сравнить эффективность вложения в различные по протяженности инвестиционные проекты (по NPV это сделать нельзя). Данный показатель показывает норму доходности/возможные затраты при вложении денежных средств в проект (в процентах).

Пример определения NPV в Excel

Для наглядности рассчитаем расчет NPV в MS Excel. Для расчета NPV используется функция =ЧПС().
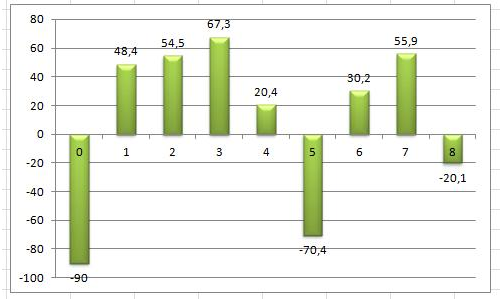
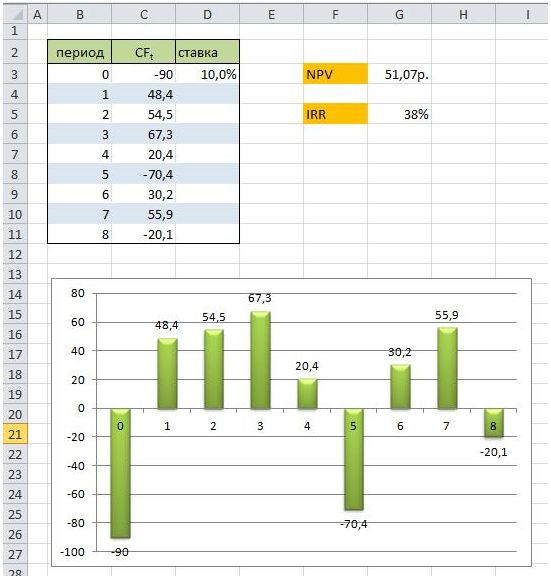
Найдем чистый дисконтированный доход (NPV) инвестиционного проекта. Необходимые инвестиции в него – 90 тыс. руб. Денежный поток, которого распределен по времени следующим образом (как на рисунке). Ставка дисконтирования равна 10%.

Анализ денежных поступлений от инвестиционного проекта

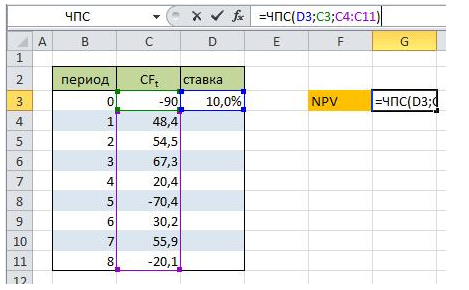
Произведем расчет чистого дисконтированного дохода по формуле excel:

Где:
D3 – ставка дисконта.
C3 – вложения в 0 периоде (наши инвестиционные затраты в проект).
C4:C11 – денежный поток проекта за 8 периодов.

Расчет NPV в Excel. Пример расчета

В итоге, показатель чистого дисконтированного дохода равен NPV=51,07 >0, что говорит о том, что есть целесообразность вложения в инвестиционный проект. К примеру, если бы мы вложили 90 тыс. руб в банк со ставкой 10% годовых, то через год получили бы чуть меньше 9 тыс., что меньше чем 51,07 от вложения в инвестиционный проект.

Мастер-класс: “Как рассчитать NPV для бизнес плана”

Пример определения IRR в Excel

Для определения IRR в Excel воспользуемся встроенной функцией =ЧИСТВНДОХ().
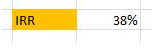
У нас в примере доход от проекта поступал в разные интервалы времени. Для этого можно использовать функцию Excel =ВСД(C3:C11). В итоге доходность от вложения в инвестиционный проект равна 38%.

Расчет IRR в Excel

В завершение картинка финансового анализа проекта целиком.

Мастер-класс: “Как рассчитать внутреннюю норму доходности для бизнес плана”

Автор: Жданов Василий Юрьевич, к.э.н.

Источник

Расчет NPV

NPV — это сокращение по первым буквам фразы «Net Present Value» и расшифровывается это как чистая приведенная (к сегодняшнему дню) стоимость. Это метод оценки инвестиционных проектов, основанный на методологии дисконтирования денежных потоков. Если вы хотите вложить деньги в перспективный бизнес-проект, то неплохо было бы для начала рассчитать NPV этого проекта. Алгоритм расчета такой:

1. нужно оценить денежные потоки от проекта — первоначальное вложение (отток) денежных средств и ожидаемые поступления (притоки) денежных средств в будущем;
2. определить стоимость капитала (англ. Cost of Capital) для вас — это будет ставкой дисконтирования;
3. продисконтировать все денежные потоки (притоки и оттоки) от проекта по ставке, которую вы оценили в п.2);
4. Сложить. Сумма всех дисконтированных потоков и будет равна NPV проекта.

Если NPV больше нуля, то проект можно принять, если NPV меньше нуля, то проект стоит отвергнуть.

Логическое обоснование метода NPV очень простое. Если NPV равно нулю, это означает, что денежные потоки от проекта достаточны, чтобы:

• возместить инвестированный капитал и
• обеспечить необходимый доход на этот капитал.

Если NPV положительный, значит, проект принесет прибыль, и чем больше величина NPV, тем прибыльнее является данный проект для инвестора. Поскольку доход кредиторов (у кого вы брали деньги в долг) фиксирован, весь доход выше этого уровня принадлежит акционерам. Если компания одобрит проект с нулевым NPV, позиция акционеров останется неизменной – компания станет больше, но цена акции не вырастет. Однако, если проект имеет положительную NPV, акционеры станут богаче.

Расчет NPV. Пример

Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам: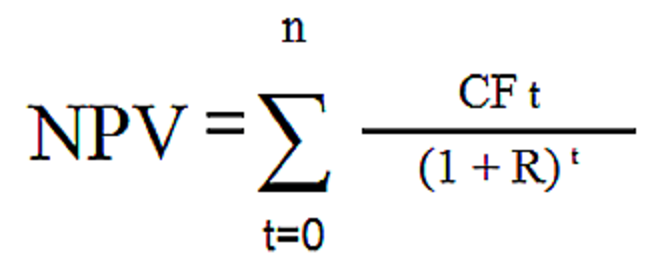
где

• n, t — количество временных периодов;
• CF — денежный поток (англ. Cash Flow);
• R — стоимость капитала, она же ставка дисконтирования (англ. Rate).

На самом деле эта формула — всего лишь правильное математическое представление суммирования нескольких величин. Чтобы рассчитать NPV, возьмем для примера два проекта A и B, которые имеют следующую структуру денежных потоков на ближайшие 4 года:

Таблица 1. Денежный поток проектов A и B.

Год	Проект A	Проект B
0	($10,000)	($10,000)
1	$5,000	$1,000
2	$4,000	$3,000
3	$3,000	$4,000
4	$1,000	$6,000

Оба проекта A и B имеют одинаковые первоначальные инвестиции в $10,000, но денежные потоки в последующие годы сильно разнятся. Проект A предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект B, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта A, но зато в последующие два года Проект B принесет больше денежных средств, чем проект A. Рассчитаем NPV инвестиционного проекта.

Для упрощения расчета предположим:

• все денежные потоки случаются в конце каждого года;
• первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас;
• стоимость капитала (ставка дисконтирования) составляет 10%.

Напомним, что для того, чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».

Применим формулу NPV для Проекта A. У нас четыре годовых периода и пять денежных потоков. Первый поток ($10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:

Если подставить в эту сумму данные из таблицы для Проекта A вместо CF и ставку 10% вместо R, то получим следующее выражение:

То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока. В результате приведенная стоимость денежных потоков для проекта A равна $788,2. Расчет NPV для проекта A можно так же представить в виде таблицы и в виде шкалы времени:

Таблиц 2. Расчет NPV для проекта A.

Год	Проект A	Ставка 10%	Фактор	Сумма
0	($10,000)	1	1	($10,000)
1	$5,000	1 / (1.10) 1	0.9091	$4,545.5
2	$4,000	1 / (1.10) 2	0.8264	$3,305.8
3	$3,000	1 / (1.10) 3	0.7513	$2,253.9
4	$1,000	1 / (1.10) 4	0.6830	$683.0
ИТОГО:	$3,000	$788.2

Рисунок 1. Расчет NPV для проекта А.

Аналогичным образом рассчитаем NPV для проекта B.

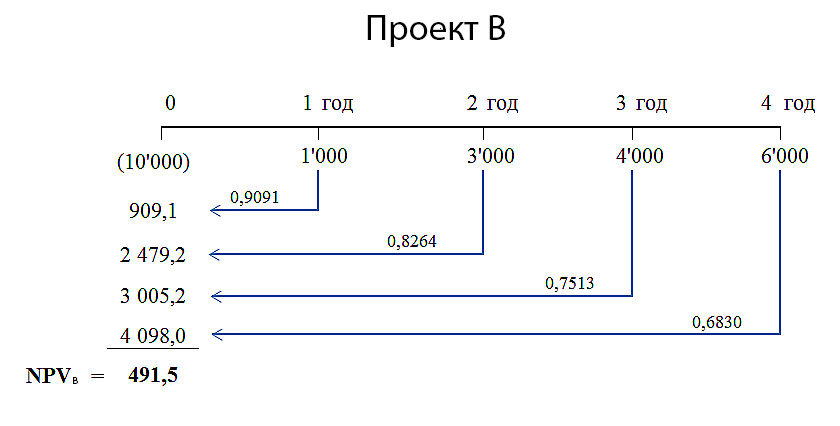
Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших ($4,000 и $6,000), но отдалённых по времени (годы 3 и 4) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта B чистая приведенная стоимость денежных потоков будет меньше, чем для проекта A. Наши расчеты NPV для проекта B дали результат — $491,5. Детальный расчет NPV для проекта B показан ниже.

Таблиц 2. Расчет NPV для проекта A.

Год	Проект B	Ставка 10%	Фактор	Сумма
0	($10,000)	1	1	($10,000)
1	$1,000	1 / (1.10) 1	0.9091	$909.1
2	$3,000	1 / (1.10) 2	0.8264	$2,479.2
3	$4,000	1 / (1.10) 3	0.7513	$3,005.2
4	$6,000	1 / (1.10) 4	0.6830	$4,098.0
ИТОГО:	$4,000	$491.5

Рисунок 2. Расчет NPV для проекта B.

Вывод

Оба эти проекта можно принять, так как NPV обоих проектов больше нуля, а, значит осуществление этих проектов приведет к увеличению доходов компании-инвестора. Если эти проекты взаимоисключающие и необходимо выбрать только один из них, то предпочтительнее выглядит проект A, поскольку его NPV=$788,2, что больше NPV=$491,5 проекта B.

Тонкости расчета NPV

Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала, то вы легко сможете подставить их в формулу и рассчитать NPV. Но на практике не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.

Денежные потоки

Самый важный и самый трудный шаг в анализе инвестиционных проектов — это оценка всех денежных потоков, связанных с проектом. Во-первых, это величина первоначальной инвестиции (оттока средств) сегодня. Во-вторых, это величины годовых притоков и оттоков денежных средств, которые ожидаются в последующие периоды.

Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.

Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.

Ставка дисконтирования

Ставка дисконтирования в формуле расчета NPV — это стоимость капитала для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы. В общем случае компания может получить финансирование из трех источников:

• взять в долг (обычно у банка);
• продать свои акции;
• использовать внутренние ресурсы (например, нераспределенную прибыль).

Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств. Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке. Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.

Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV) будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC (Weighted Average Cost of Capital), что переводится как средневзвешенная стоимость капитала.

Зависимость NPV проекта от ставки дисконтирования

Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала. Давайте рассчитаем NPV по проектам A и B для разных ставок дисконтирования:

Стоимость капитала, %	NPV A	NPV B
0	$3,000	$4,000
2	$2,497.4	$3,176.3
4	$2,027.7	$2,420.0
6	$1,587.9	$1,724.4
8	$1,175.5	$1,083.5
10	$788.2	$491.5
12	$423.9	($55.3)
14	$80.8	($562.0)
16	($242.7)	($1,032.1)
18	($548.3)	($1,468.7)

Таблица 3. Зависимость NPV от ставки дисконтирования.

Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):

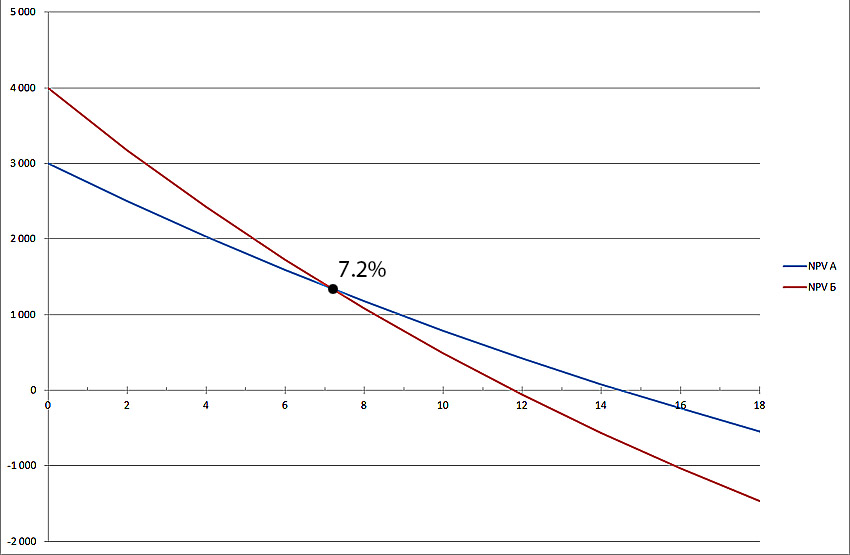
Рисунок 3. Зависимость NPV от ставки дисконтирования.

Из графика видно, что NPV проекта A превышает NPV проекта B при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.

Кроме того, из графика также видно, что проект B является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта B уменьшается быстрее по мере роста этой ставки. И это легко объяснимо. В проекте B денежные поступления в первые годы проекта невелики, со временем они увеличиваются. Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.

Например, можно рассчитать, чему будут равны $10,000 через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения.

Таблица 4. Зависимость NPV от времени его возникновения.

Год	Ставка 5%	Ставка 10%	Разница, $	Разница, %
1	$9,524	$9,091	$433	4.5%
4	$8,227	$6,830	$1,397	17.0%
10	$6,139	$3,855	$2,284	37.2%

В последнем столбце таблицы видно, что один и тот же денежный поток ($10,000) при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37.2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать.

Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.

Источник