логарифм цены
Зачем нужен логарифм цены? Логарифм цены позволяет уйти от искажений, связанных с абсолютными значениями цены и перейти к относительной оценке. Это имеет значение в инвестициях и трейдинге, поскольку для инвестора имеет значение не столько, сколько стоит акция $10 или $100, сколько относительное изменение цены за интервал времени[1].
На логарифмическом графике цены при изменении цены в большом диапазоне, например от $1 до $1000, равную высоту будут иметь свечи с одинаковым процентным изменением, а не с одинаковым изменением в долларах .
Инвесторов должны беспокоить прежде всего логарифмы цен, потому что они лучше отражают то, как инвесторы воспринимают свои прибыли и убытки. Тезис об этом впервые сформулировал Маури Осборн в 1959 году.
Простое объяснение: «смысл логарифма — что люди мыслят в терминологии «выросло в два раза», и не важно от каких уровней. Чтобы уровнять рост в два раза от разных уровней и используют логарифм» [2]
Логарифмированные ценовые ряды удобно использовать из-за известного свойства log(b)-log(a)=log(b/a), то есть разница логарифмов двух цен a и b = логарифму относительного приращения b/a, то есть логарифму доходности. Таким образом если взять логарифмы цен и потом каждый предыдущий член ряда вычесть из последующего, то получатся логарифмы доходности. Это удобно чисто практически[3].
Логарифм цены обладает чудесным свойством: разница между Log(10) и Log(11) равна разнице между (Log100)-Log(110).
Так и доходность акции которая поднимается с 10 до 11 эквивалентна доходности акции которая выросла со 100 до 110.
Кроме того, логарифмы цен берут по следующим причинам:
- математически логарифмирование заменяет умножение сложением. С точки зрения теории случайных процессов, логарифмы приращений цен Гауссовы, а Гауссова случайная величина более проста и исследована. Таким образом, происходит упрощение
- с помощью логарифма можно суммировать доходности за разные промежутки времени (например для fixed income инструментов). Доходности удобно складывать с помощью логарифма т.к. сумма двух одинаковых по основанию логарифмов равна логарифму произведения
Почему логарифм приращения цен используется в статистических исследованиях вместо обычного относительного приращения цен?
Приращение цены в процентах обычно считается как (P2-P1)/P1, однако, данный способ имеет недостаток, т.е. если цена уменьшилась на 5%, а затем увеличилась на 5% мы не получим первоначальное значение. Логарифмическая доходность не имеет этого недостатка, при этом если взять первый член ряда Маклорена от функции Ln(Р2/Р1), будем иметь Р2/Р1 — 1, т.е. тоже самое, что и обычная доходность и при малых изменениях это будет одно и тоже.[4]
Источник
Рыночные инварианты, или Зачем трейдеру логарифмы
Термином «инвариант» в науке принято обозначать величину остающуюся неизменной при тех или иных преобразованиях объекта. К примеру, внешность человека может очень сильно меняться под воздействием возраста, грима или пластической хирургии, но его всегда можно опознать по ДНК. Код ДНК является инвариантом – неизменной характеристикой. Инварианты часто несут наиболее важную информацию о том или ином предмете или явлении.Какое отношение все это имеет к финансовым рынкам? Финансовые рынки хорошо известны своей необычайной подвижностью. Цены большинства инструментов меняются, чуть ли не ежесекундно. Естественным образом возникает вопрос: есть ли что-то неизменное в этом море хаоса и нестабильности?
Цена учла все… и заблудилась
Известный постулат технического анализа гласит: «Цена учитывает все». Многие трейдеры поэтому важнейшей характеристикой фининструмента считают его цену. Можно ли признать цену рыночным инвариантом? Не смотря на всю экономическую важность понятия «цена», ответ на этот вопрос отрицательный. Цена постоянно меняется, значит, по определению она не может быть инвариантом. А что же средняя цена? Скользящие средние – один из наиболее популярных методов анализа. Возможно, средняя цена демонстрирует качество неизменности и устойчивости? Оказывается, нет. В этом можно наглядно убедиться из следующей картинки.
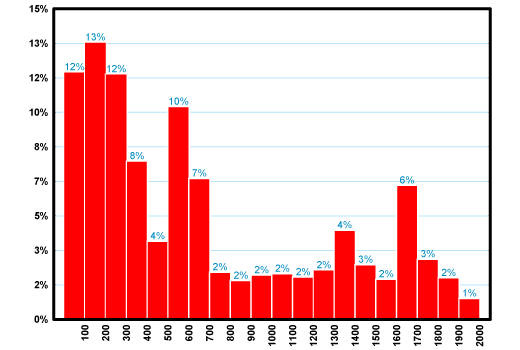
На ней представлена гистограмма дневных «цен» закрытия индекса ММВБ с 1998 по 2009 год. Значения индекса в этот период колебались от минимального 18.53 до максимального 1969.91. Средняя цена составляла 669.19. Гистограмма показывает процент попаданий наблюдаемой цены по интервалам. Напр., в диапазоне от 100 до 200 (пик гистограммы) цена индекса находилась 13% времени, а в интервале от 0 до 300: 12% + 13% + 12% = 37%. Фактически гистограмма цены имеет случайный характер. Никаких сколько-либо выраженных закономерностей на ней не наблюдается. Средняя цена 669.19 не является самой частой, типичной. Это просто формальное число. Подобную картину можно наблюдать, если построить гистограмму любого другого фондового индекса или акции.
Связано это с тем, что динамика цен многих инструментов неплохо описывается моделью так называемого «случайного блуждания со сносом». Возьмите тетрадку в клеточку. Киньте монетку. Если выпадет «орел», нарисуйте «свечку» вверх на две клеточки, если «решка» – на две клеточки вниз. Независимо от выпадения монеты всегда приплюсовывайте и к бычьей и к медвежьей свечке одну клеточку вверх – это и есть «снос» или, другими словами, тренд. Если не полениться и провести множество бросаний монеты, полученный график будет довольно похож на график цены какой-нибудь акции. При помощи компьютера можно добиться еще большего реализма, генерируя свечи вверх и вниз случайного размера. Гистограмма цены не содержит какого-либо выраженного паттерна по причине ее случайного блуждания. Нет никаких экономических механизмов, которые бы возвращали цену акции к ее среднему значению. По этой причине она блуждает сама по себе обычно с некоторым положительным трендом. Средняя цена, таким образом, не может быть инвариантом. Продолжим поиск…
Добавим смысла
Что если вместо самой цены рассматривать ее дневные приращения? Например, вместо самого значения индекса брать его дневные изменения в пунктах. Для акции это будет дневное изменение цены в рублях или долларах – логика при этом такая же.
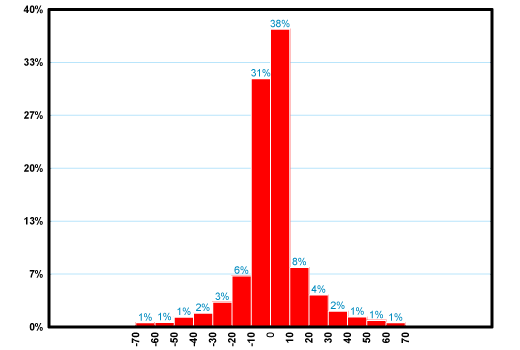
Гистограмма теперь имеет осмысленный вид. Среднее значение дневного приращения индекса – 0.43 пункта находится вблизи пика. В частности в интервал от -10 до +10 пунктов попадают 69% наблюдений. Таким образом, среднее приращение цены – это действительно наиболее ожидаемая величина (или очень близкая к ней).
Линейная доходность
Тем не менее, среднее изменение цены нельзя признать инвариантом. По мере роста цены акции или уровня индекса диапазон ее колебаний также будет расти. Допустим, некоторая акция торгуется сейчас в районе 10 рублей. Тогда увеличение ее цены на 1 рубль будет составлять 10%. Предположим, через несколько лет акция выросла до 100 рублей. Рост на 1 рубль для нее будет уже только 1%. Один рубль для 10-рублевой и 100-рублевой акции – совсем разные вещи, поэтому инвесторы ориентируются не на денежную, а на процентную доходность, т.е. не на абсолютные, а на относительные величины. Процентная доходность не зависит от текущего уровня цен. Она более устойчива и, следовательно, более достойна звания инварианта. Рассчитать процентную доходность очень просто. Для этого нужно знать лишь цену открытия (O) и цену закрытия (C):
Вообще говоря, доходность не является полностью статичной и меняется от года к году. В один год акция может давать 10%, в другой 15%, а в третий -20%. Однако в очень долгосрочной перспективе можно предположить, что средняя доходность фондовых рынков стабильна и не зависит от времени. Например, старейший фондовый индекс Доу Джонса за последние 80 лет в среднем показывал доходность около 4.5% годовых. Таким образом, в самом общем случае от американского фондового рынка можно ожидать такую цифру доходности.
Процентная доходность на первый взгляд кажется наиболее естественно характеристикой фининструмента. Она не зависит от уровня цены. Кроме того, на ней очень интуитивно отражается влияние кредитного плеча – она просто умножается на коэффициент рычага: 1% доходность при плече 1:2 превращается в 2% и т.п. По этой причине ее еще называют линейной доходностью, поскольку рычаг воздействует на нее линейным образом.
Однако линейная доходность имеет один недостаток. Цена не может быть отрицательным числом, а доходность не может быть меньше -1 (-100%). Это создает перекос в распределении линейной доходности. Он становится особенно заметен при больших цифрах. Напр., 100% росту соответствует 50% падение, а не 100% падение, как может ошибочно подумать новичок. Это легко проверить. 100-рублевая акция вырастает в 2 раза до 200 р.: 100*2 = 100*(1+1) = 200. Это рост на 100%. Чтобы вернуть ее обратно к 100 рублям, нужно 200 р. разделить на 2 или умножить на 0.5: 200/2 = 200*(1 — 0.5) = 100. Это 50% падение. Диапазон линейной доходности (от -1 до бесконечности) несимметричен относительно нуля, и эта асимметрия никак не связана с вероятностными свойствами цены, поэтому, по сути, она имеет искусственный характер. Как же ее устранить?
Логдоходность
Логарифмическая доходность (или просто логдоходность) лишена этого недостатка линейной доходности. Она рассчитывается по формуле:
и принимает значения от «минус» до «плюс бесконечности». Символ ln() обознает функцию натурального логарифма. Что это за функция? В математике кроме знаменитого числа π есть еще и число e. Оно приблизительно равно 2.7183. Натуральный логарифм – это степень, в которую нужно возвести число e, чтобы получить число под знаком логарифма. Например, если число e, 2.7183, возвести в квадрат (степень 2), получится: 2.71832 2 = 7.3891. Отсюда следует, что ln(7.3891) = 2. Собственно, чтобы пользоваться логарифмами, не обязательно знать все эти тонкости. Функция логарифма является стандартной, ее легко можно вычислить на компьютере, пользуясь калькулятором Windows или Excel и т.п.
Логдоходности удобны тем, что их можно складывать. Допустим, известны 5 дневных обычных доходностей за торговую неделю: 1%, -2%, 3%, -1%, 2%. Надо найти недельную доходность. Для этого нужно разделить доходности на 100%, прибавить к ним единицу и перемножить:
За неделю цена выросла на 2.95%. Умножение, однако, не очень удобная и интуитивная операция. Если перейти к логдоходностям, можно заменить ее сложением:
0.0100 -0.0202 + 0.0296 -0.0101 + 0.0198 = 0.0291
Недельная логдоходность составляет 2.91%. Логдоходность всегда меньше обычной доходности. Величина этого различия становится заметной лишь при больших цифрах. К примеру, линейной доходности -50% соответствует логдоходность -69%, а -100% – «минус бесконечность».
Дорога домой
Итак, в поисках инвариантов мы проделали довольно долгий путь от цены, через ее приращения и линейные доходности к такой довольно абстрактной вещи как логдоходность. Гистограмма логдоходности как и гистограмма приращений имеет выраженный пик, поэтому средняя логдоходность является и наиболее ожидаемой, наиболее вероятной. Она, как и линейная доходность, не зависит от текущего уровня цен. И, наконец, она симметрична относительно нуля, поскольку может принимать любые отрицательные и положительные значения. Все это позволяют охарактеризовать ее как натуральный рыночный инвариант. Превратить же цены в логдоходности достаточно просто при помощи MATLAB, Excel или других табличных редакторов.
Сейчас существует большое количество программ для прогнозирования адресованных трейдерам, например, нейросетевых. Они просты в управлении и не требуют специальных знаний. Типичная ошибка новичка при использовании такого софта в том, что он пытается «предсказать» непосредственно будущую цену по прошлым ценам. Однако, как мы убедились, изучив гистограмму, прогнозирование самой цены «в лоб» лишено какого-либо вероятностного смысла. Лучше всего прогнозировать будущую логдоходность по прошлым логдоходностям того же самого инструмента или других инструментов, если предполагается межрыночное взаимодействие. Это максимально упростит работу программе, поскольку ей не надо будет тратить силы на поиск очевидных закономерностей: что приращения цены зависят от ее уровня, и что они скошены в положительную сторону.
Хорошо, допустим, все это сделано, и программа выдает прогноз: завтрашняя дневная логдоходность составит 0.03. Как это понимать и использовать на практике? Необходимо конвертировать прогноз логдоходности в прогноз цены при помощи обратного преобразования. Делается это очень просто. Предположим, что текущая цена акции 100 рублей. Тогда прогноз завтрашней цены можно получить по формуле:
100 р.*exp(0.03) = 100 р.*1.0305 = 103.05 р.
Функция exp() – это уже знакомое нам число e в степени икс. Это просто альтернативный вариант записи, часто используемый в компьютерных приложениях. Экспонента является обратной по отношению к логарифму функцией, поэтому, подставляя в нее логдоходность, сразу же получаем коэффициент роста, на него и надо умножить текущую цену, чтобы получить прогноз будущей.
Резюме
Таким образом, мы убедились, что логдоходности – очень удобный аналитический инструмент. Их можно складывать, они не зависят от уровня цен и симметричны относительно нуля. На практике, если нужно получить прогноз или исследовать какие-либо вероятности движения цен следует использовать именно логдоходности.
Логдоходности легко конвертируются из одного тайм-фрейма в другой. Например, если вы хотите перевести дневную логдоходность в годовую, нужно просто умножить ее на количество торговых дней (около 250). Если затем взять экспоненту от этого числа, будет получен годовой темп роста капитала для торговой стратегии. Его удобно сравнивать с текущими банковскими ставками, доходностью фондовых индексов и других эталонных инструментов.
————————————————————————
Источник
Как рассчитать логарифмическую доходность
логарифмическая доходность
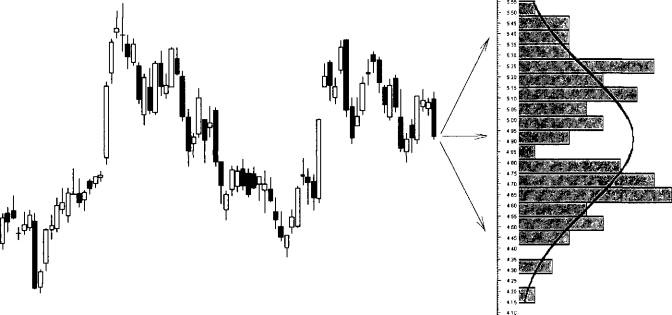
Для анализа также еще используют данные об изменении цен либо логарифмическую доходность — отношение логарифмов, обычно натуральных, цен изучаемого ряда. Мы не будем проникать в дебри статистического анализа, выясняя тип распределения на рисунке 1 — 1, поскольку этот вопрос слишком большой, и для нас он сейчас не слишком важен. Заметим, по-видимому, в данном случае мы имеем дело с распределением Парето либо Стьюдента, подклассом которого является нормальное распределение. В распространенных опционных моделях обычно основываются на логнормальном, или логарифмически-нормальном распределении: распределении случайной величины, логарифм которой характеризуется нормальным распределением. В связи с этим следует отметить, что предположение о нормальности или лог-нормальности распределения ценовых рядов достаточно условно: строгое использование гипотезы о нормальности распределения вовлечет в модель ценообразования отрицательные цены.
Фактически кривая распределения цен показывает нам вероятность достижения в будущем ценой интересующего нас значения. Математическое моделирование позволяет ввести различные предположения относительно формы распределения, а также продолжить «хвосты» в обе стороны, которые для рассматриваемого ценового ряда относятся к разряду стресс-ситуаций. Тем не менее, их обычно учитывают в моделях, вводя ограничения через параметр доверительного уровня, принимающего разные значения в зависимости от выдвигаемых предположений и методологии расчетов.
Очевидно: чем больше срок действия опциона, тем дальше от текущих значений могут сдвинуться цены, поэтому премия опциона растет с увеличением срока до истечения. Собственно, премия опциона определяется суммированием результатов всех исходов, взвешенных по вероятности, корректируемых по ставке, чтобы получить приведенную стоимость. Так как опцион — всего лишь одна из инвестиционных альтернатив, то приходится учитывать влияние арбитража, устраняющего рыночные диспропорции с помощью разнообразных, но связанных между собой финансовых инструментов. Все вычислительные расчеты, необходимые для определения опционной премии, которую иногда называют «справедливой», говоря о теоретических ценах, как раз и выполняют многочисленные модели ценообразования опционов.
Рис. 1-1. Дневной график цен РАО «ЕЭС России» (ММВБ) за четыре месяца, а также распределение цен
Следует отметить: в реальности определить, что такое «справедливая цена», — очень сложно, если вообще возможно. В принципе, это весьма эфемерная величина, поскольку некоторые параметры для модели берутся непосредственно из рынка, поэтому любые текущие цены являются по большому счету «справедливыми», вне зависимости от обстоятельств. Единственное, что можно предположить — это возможность ошибки рыночных игроков, переоценивших рынок в данный момент времени или недооценивших его.
Подводя итог, остается заметить: физический смысл опционной премии в том, что она показывает, сколько инвестор готов заплатить в текущий момент времени за право обладания рисковым активом. Собственно, эта задача, получившая название «Петербургский парадокс», известна более четверти тысячелетия и впервые была поставлена Бернулли, затем и решившим ее.
Статья размещена в рубрике: Риск менеджмент
Источник