Как рассчитать годовую доходность сделки

Что такое доходность? Формула расчета доходности

Итак, что же такое доходность и какова формула доходности?
Доходность — один из главных показателей инвестиций, по которому можно оценивать выгодность инвестиций, их целесообразность и сравнивать их между собой по этому показателю. Часто для оценки выгодности вложения денег используют связку риск-доходность. Логика здесь проста: сами по себе такие показатели, как доходность и риск малоинформативны. Какой смысл вкладывать деньги в инструменты с высоким уровнем риска и низкой потенциальной доходностью? Если риск убытков велик, то и возможное вознаграждение должно быть на высоком уровне.

Отделим понятия дохода и доходности. Доход — это абсолютная величина, выраженная например, в денежных единицах (Вася вложил 10 000 руб. и получил доход 2 000 руб.) В то время как доходность — относительная величина, выражаемая в процентах или процентах годовых, об этом позже (Саша вложил свои деньги в коммерческую недвижимость с доходностью 25% годовых).

Формула расчета доходности

Далее будет материал с формулами, но не бойтесь — любой человек, учившийся в школе в них разберётся — они просты для понимания. Кроме того, в вашем браузере должно быть включено отображение картинок, поскольку формулы приведены в виде рисунков.

Простейшая формула доходности представляет собой отношение полученной прибыли к сумме вложений, умноженное на сто:

Также доходность можно посчитать, если известна начальная и конечная сумма вложений:

где сумма1 — начальная сумма,
сумма2 — конечная сумма.

Однако, в этих формулах не учитывается такой важный показатель, как время. За какой период эта доходность? За 100 лет? Или за 3 месяца? Чтобы учесть время, за которое инвестиции показали доходность, используется следующая формула доходности:

где срок в месяцах — время, в течение которого происходит вложение средств.

Калькулятор накоплений

Самый распространённый период расчёта доходности — 1 год (за примерами далеко ходить не надо — те же банковские вклады считаются в процентах годовых).

Что такое доходность? Примеры расчета доходности

Приведём примеры для того, чтобы лучше понять, как рассчитывается доходность.

Пример 1. У Людвига Аристарховича есть недвижимость стоимостью 2.000.000 руб, он сдаёт её в аренду за ежемесячную плату 10.000 руб. Какова доходность его вложений за год (в процентах годовых)?

Пример 2. Иннокентий — удачливый Форекс-трейдер: он начал торговать, имея депозит $1000. Через 10 месяцев он удвоил свой депозит. Какая годовая доходность торговли на форексе получилась у Иннокентия?

Применение доходности

Таким образом, доходность показывает на сколько процентов выросла вложенная сумма или увеличился капитал (а также сколько процентов прибыли принёс актив). Доходность можно рассчитать как за всё время, так и за определённый период (например год).

Годовая доходность — важный параметр, по которому инвесторы могут делать выводы о привлекательности того или иного инструмента вложений. Также можно сравнивать разные способы вложений между собой по среднегодовой доходности.

Источник

Цифры, числа и проценты — как правильно считать прибыль и годовую доходность | Несколько простых способов с интересными примерами

Проходили в школу простые и сложные проценты? Ну как вам? Скукотища. Какие-то цифры, числа. Математические действия: умножение, деление, вычитание и сложение. Но все меняется, когда речь идет о деньгах. Собственных деньгах. Потенциале их роста от инвестиций. Сразу происходит смена настроения абсолютно на противоположное. От просто скучно до интересно.

И самыми любимыми становятся сложение и умножение. Складывать (суммировать) капитал и приумножать (зарабатывать) прибыль.

Расскажу про пару способов и приемов, как можно достаточно просто и быстро оценивать и считать результаты вложений (будущие и реальные). И главное, правильно.

Есть еще люди «в наших селеньях», кто не знает (или просто забыл) как все это делается.

Нам нужен калькулятор и один палец (не показывать, а нажимать на кнопки). В некоторых случаях просто мозги.

Складываем годовые доходности

Вы получили в первый год прибыль в 10%, во второй снова 10%. А на третий год? . опять десять.

Внимание вопрос. Сколько вы заработали за 3 года?

Быстрый ответ — 30% прибыли.

Мы посчитали 30% по правилам простых процентов. Просто сложив их вместе.

Если срок короткий и (или) доходность небольшая (не 20-30 и тем более не 50-100%), то результат будет близок к истине. Но как вы поняли, неправильный.

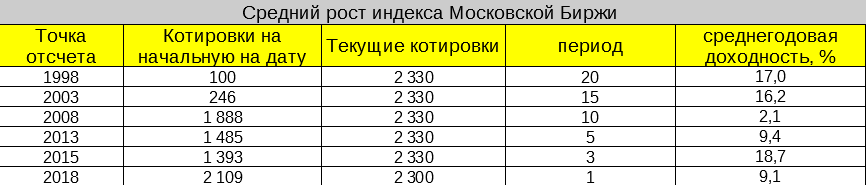
Представьте, что в течение 7 лет вы получаете по 10% годовых на вложенный капитал. Пусть будет на 100 тысяч.

Сколько мы заработаем за этот срок?

Снова быстрый ответ: 70% прибыли или 70 тысяч.

На самом деле — 95 тысяч рублей. Вы только что потеряли (недосчитали) 25 000.

Доходности нужно не складывать, а умножать между собой.

10% со 100 рублей, дадут 10. В совокупности будет 110.

Во второй год 10% берем со 110 — 11. Получаем в итоге — 121 рубль.

Третий год — принесет нам 12,1. Итого — 133,1 рубль.

Как это все подсчитать?

Проценты преобразуем по формуле: 1+ (доходность за год/100%). И перемножаем.

Соответственно 20% — это будет 1.2; 30% -1.3; 45% — 1.45.

В нашем случае: 1,1 х 1,1 х 1,1 и так далее. семь раз.

Правила расчета простых и сложных процентов

Прибыль + убытки — как сложить?

Как сложить между собой прибыльные и убыточные периоды?

Простой вопрос. В первый год получили прибыль +10% . За второй убыток -10% . Сколько денег будет в итоге?

Вроде бы плюс на минус дает ноль. Десять туда, 10% обратно.

Мы в той же точке отсчета.

На самом деле мы потеряли 1% (можете проверить на калькуляторе).

Причем последовательность не важна. Получена сначала прибыль, потом убыток. Или наоборот. Результат будет один.

Как быстро подсчитать?

• 10 процентов прибыли — 1,1;
• 10% убытка — 0,9.

Формула: 1- (убыток за период/100).

Перемножаем числа между собой и получаем результат.

В нашем случае: 1.1 Х 0.9 = 0,99. Или 99% от первоначального капитала.

Методы 72

Метод семидесяти двух позволяет быстро узнать, через сколько лет ваши вложения удвоятся.

Для этого нужно число 72 разделить на ожидаемую годовую доходность.

Например, при ежегодной прибыли в 7% — вы удвоите капитал примерно через 10 лет.

Увеличиваем доходность до 14,4% — и каждые 5 лет получаем прибыль 100%.

Через 10 лет у вас будет в четыре раза больше денег, через 15 — в 8 раз, через 20 — в 16.

Ну а «потерпев» 30 лет — вы увеличите свой капитал в 64 раза.

Метод 72 не блещет математической точностью. Всегда есть небольшая погрешность. Но на лету быстро посчитать и получить приблизительный результат — самое оно.

Кстати формула работает и в обратном направлении.

Ежегодный убыток в 6%, примерно через 12 лет ополовинит ваш капитал.

Интересно это использовать при инфляции. Насколько уменьшается покупательная способность денег.

Средняя инфляции в РФ за последние десять лет составила 7,43%.

Это значит, что рубль «усох» в 2 раза за 9,5 лет.

Метод 114

Все аналогично способу подсчета 72 (делим 114 на годовой доход). Но формула показывает утроение капитала за период. Тоже с небольшой погрешностью.

Пара примеров утроения капитала.

При доходности в год:

• 8% | (114 / 8) = 14,2 года
• 10% | (114 / 10) = 11,4 года
• 12% | (114 / 12) = 9,5 лет
• 14% | (114 / 14) = 8,1 год.

Среднегодовая прибыль за несколько лет

Как посчитать среднегодовую прибыль за различные периоды? А зачем?

Начнем с примера. Дальше поймете, нужна вам эта инфа или нет.

Два инвестора Вася и Петя начинаются мериться своими достоинствами доходностями. У кого больше. И кто круче.

Вася: Я раскачал свои 250 тысяч за 5 лет до 580 кусков. Заработал 330 000 рублей прибыли.

Петя: Мои скромные 40 тысяч я превратил в сотку всего за 6 лет. Прибыль 60 тысяч.

А кто из них действительно в большем плюсе от суммы вложенного капитала. У кого прибыль в процентах выше?

Вася за 5 лет получил 132% прибыли.

Петя заработал 150%, но за 6 лет.

Можно выделить среднегодовую доходность и увидеть, кто зарабатывал в год больше. Делим общий процент прибыли на количество лет.

Вроде бы Вася круче. У него больше. Хоть и ненамного.)))

Но мы немного неправильно вычленили годовую доходность.

Среднегодовая доходность = n√(Pn/P0)-1; где

• n — количество периодов (лет);
• P0 — начальное значение капитала;
• Pn — конечное размер

УУУУ. Какие-то корни. И даже не квадратные. И еще не все калькуляторы это поддерживают. Забудьте ее навсегда.

Мне больше нравится считать в электронных таблицах (Excel вам в помощь).

Есть такая формула.

=степень (Pn/P0; 1/n) — 1

Вносим 3 параметра — начальный, конечный капитал и срок вложений.

Получаем:

Рост за 6 лет у Пети с 40 до 100 тысяч соответствует среднегодовой доходности в 16,5%.

Вася, получивший сверху 330 тысяч за 5 лет зарабатывал в среднем по 18,3%.

Обратите внимание, как кардинально поменялись результаты по сравнению с простым делением общей прибыли на количество лет.

И наш «крутыш» Вася хоть и остается в лидерах, но среднегодовая прибыль уменьшилась почти в 1,5 раза..

Где еще можно применять такую формулу?

Для примера несколько вариантов использования.

Биржевые графики

Смотрим на какой нибудь биржевой график (акции, индекс, ETF). Нам нужно примерно оценить как он растет в среднем в год. На сколько процентов?

Например, за последние 5, 10, 20, 30 лет (да хоть сто лет).

Можно конечно поискать информацию в интернете. Есть различные статистические данные. Таблицы. Красивые цифры.

Но мы легкие пути не ищем. Рассчитаем все сами.

Нам нужна бутылка водки (хотя можно и без нее обойтись), начальная и конечная цена за требуемый период.

И электронная таблица. Особенно, если есть какой-то готовый шаблон — дело пары секунд (Спойлер: шаблон есть ниже). Вносим 3 числа и результат моментально перед глазами.

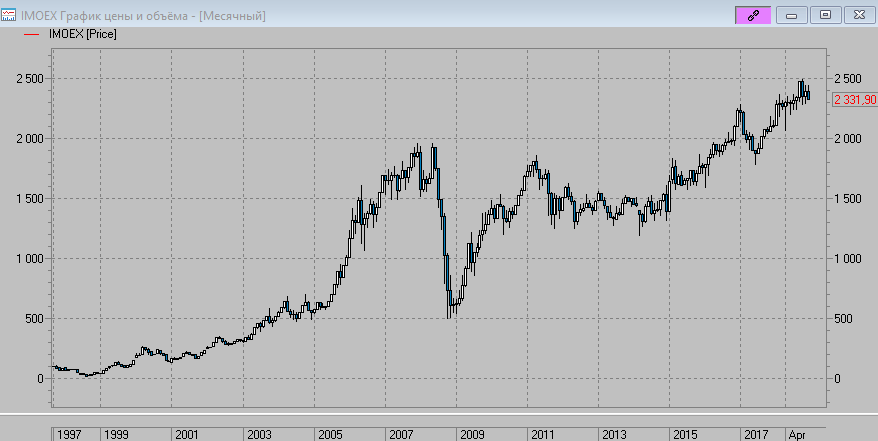
Для примера возьмем наш любимый и родной индекс Московской биржи. С момента его основание и по текущий момент.

Текущий (2018 год) еще правда не закончился (конец декабря). Но это не сильно критично.

В таблице видно на сколько процентов в среднем рос рынок в зависимости от точки входа.

Интересный момент с удорожанием продуктов.

Стоила лет десять назад булка хлеба 10 рублей. А сейчас ее цена 35 рубликов.

Молоко продавали за 20, а сейчас за 60 (данные я взял с потолка, просто для примера).

И так понятно, что грабеж среди бела дня. Но как его подсчитать?

Забиваем данные в таблицу и видим, что хлеб дорожал в среднем на 13,3% в год. А молоко всего на 11,6%.

Чего нам ждать в будущем: выравнивание пропорции цен? Хлеб стоит явно дороже, чем должен. Значит . скоро цены на него снизятся. ))))

А может на молочко еще подрастут (что более вероятно).

Дивиденды

Вернее темпы их роста. Интересная штука, скажу я вам.

Дивидендные аристократы (обычно компании из Америки) из года в год стараются повышать уровень выплат для своих акционеров. В России есть немного таких компаний, действующих подобных образом.

Вот статистика выплат дивидендов за последние несколько лет.

Лукойл — Дивиденды по годам

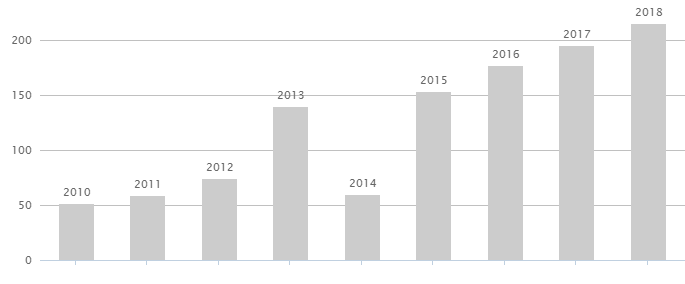
За восемь лет, размер дивидендов вырос со скромных 52 рубля на акцию в 2010, до 215 рублей в 2018 году. Ежу понятно, что это уже неплохо. Но . насколько неплохо?

С помощью формулы, можно определить среднегодовой темп прироста дивидендов.

Получаем 19,4% в год. Рост прибыли только за счет дивидендов. (Котировки на акции Лукойл тоже за это время выросли порядком). Обгоняющий инфляцию минимум в 2 раза.

Ради интереса рассчитал темпы роста дивов по другим голубым фишкам российского рынка: Газпром, Сбербанк и МТС.

Очень любопытная картина получилась.

Среднегодовой рост дивидендов

По старой традиции для ленивых (или тех кто ценит свое время) прикладываю файл со всем, что здесь было написано, описано, рассчитано. Может кому и пригодится. При необходимости переделайте под себя.

Всем удачных (и правильно подсчитанных) положительных доходностей!

За обновлениями в этой и других статьях теперь можно следить на Telegram-канале: @vsedengy.

Источник

Расчет годовой доходности и стандартного отклонения

Автор: Дмитрий Никитенко
Дата записи

Чтобы вы всегда могли проверить данные, найденные в интернете, или рассчитать доходность собственных инвестиций, в этой статье я научу вас делать это правильно.

Приведенные здесь методы расчета подходят для любых электронных таблиц – Excel, Google Sheets или LibreOffice. А то, что не использует экселевские функции, можно просто считать в любом калькуляторе, например, встроенном в Google или Яндекс.

Расчет доходности инвестиций

Доходность в процентах за любой период можно рассчитать двумя способами:

1. знакомая многим формула: (конец периода — начало периода) / начало периода = (110 — 100) / 100 = 10%;
2. и более короткая версия: конец периода / начало периода — 1 = 110 / 100 — 1 = 10%. Мы будем считать доходность за год по второй формуле, потому что она немного короче и её результат в разах (до вычитания единицы) нам ещё пригодится.

Дальше для простоты мы будем называть её общей доходностью.

Расчет средней годовой доходности (и приведение доходности к годовой)

Под средней годовой доходностью обычно понимается среднегодовая ставка доходности, которая приводит начальную сумму вложений к конечной путем последовательного начисления этой ставки на результат предыдущего года.

Это не просто средняя арифметическая доходностей отдельных лет, а среднее геометрическое. Проще говоря, какую прибыль в процентах вы должны каждый год получать, чтобы из суммы А в итоге получилась сумма Б.

Средняя геометрическая доходность учитывает эффект сложного процента (капитализации процентов и возникающего в следствие этого экспоненциального роста), поэтому всегда будет меньше арифметической средней.

Другое название средней геометрической доходности из англоязычных источников, которое вам может встречаться — “compound annual growth rate” (CAGR).

Рассмотрим расчет годовой доходности для нескольких видов входящих данных, которые обычно имеют инвесторы. Под среднегодовой доходностью далее будем понимать именно среднюю геометрическую или CAGR.

Есть общая доходность за период

Если известно какую доходность принес актив за весь период, годовую доходность можно найти по формуле:

где x – доходность за весь период в процентах, n – количество полных лет в периоде, ^ – возведение в степень.

Например, если за 3 года доходность составила 30%, то среднегодовая доходность будет равно не 30% / 3 = 10%, а (0.3 + 1) ^ (1 / 3) — 1 = 9,14%.

Проверим: начальная сумма 100, конечная – 130:

• 100 + 100 * 9,14% = 109,14
• 109,14 + 109,14 * 9,14% = 119,12
• 119,12 + 119,12 * 9,14% = 130

Прибавление единицы нужно, чтобы перевести известную доходность из процентов в разы, а вычитание в конце – для перевода обратно из разов в проценты (напомню, что 30% = 0.3, в Excel можно записать оба варианта, разницы нет).

В Excel (или других электронных таблицах) возвести в степень можно либо с помощью того же знака ^, либо функцией СТЕПЕНЬ((x + 1); (1 / n)) — 1.

Есть начальная и конечная сумма

Если у вас есть результат инвестиций за известный период в виде сумм на начало и конец этого периода, то всё, что нужно сделать – это узнать общую доходность (формула та же, из начала статьи – 130 / 100 — 1 = 30%) и с ней рассчитать среднегодовую по формуле из предыдущего пункта.

Есть доходности по годам

Если у вас есть ряд доходностей за отдельные годы или вы можете найти их по ценам, то расчет среднегодовой доходности сводится к двум способам:

1. поиску среднего геометрического этих доходностей, выраженных в разах;
2. умножению этих разов для получения общей доходности и расчету как в предыдущих пунктах.

Первый вариант считать вручную нет смысла, поэтому лучше сразу обратиться к Excel и воспользоваться функцией СРГЕОМ (GEOMEAN). В неё надо передать либо список значений, либо диапазон ячеек, в которых у вас записаны годовые доходности, выраженные в разах.

Для примера посчитаем так инфляцию в России за последние 5 лет:

• 2014: 11,35% + 1 = 1,1135
• 2015: 12,91% + 1 = 1,1291
• 2016: 5,39% + 1 = 1,0539
• 2017: 2,51% + 1 = 1,0251
• 2018: 4,26% + 1 = 1,0426

СРГЕОМ(1,1135; 1,1291; 1,0539; 1,0251; 1,0426) — 1 = 7,2%

СРГЕОМ(A1:A5) — 1 = 7,2% (представим, что в ячейках те же доходности в разах)

Второй вариант расчета через умножение будет выглядеть так:

(1,1135 * 1,1291 * 1,0539 * 1,0251 * 1,0426) ^ (1 / 5) — 1 = 7,2%

Есть доходность за неполный год

Пока мы рассмотрели только полные годовые периоды, но среднегодовую доходность можно считать и для неполных лет. Например, какой-то актив за 4 года и 6 месяцев принес вам 50%. Чтобы аннуализировать эту доходность (привести к среднегодовой, в степень нужно подставить 4,5:

(0.5 + 1) ^ (1 / 4,5) — 1 = 9,43%

Привести месяцы неполного года к дробной части можно просто разделив их на 12:

• 6 / 12 = 0,5;
• 8 / 12 = 0,67 и так далее.

По аналогичному принципу можно взять доходность за прошедшее количество дней в году и привести её к годовой:

(x + 1) ^ (252 / n) — 1, где x – доходность за эти дни в процентах, n – количество дней, а 252 — количество торговых дней в году.

Если доходность за 100 дней года составила 3%, то среднегодовая будет равна:

(0,03 + 1) ^ (252 / 100) — 1 = 7,7%.

Вместо торговых дней можно брать и календарные, то есть 365 — выбор зависит от ваших данных и целей расчета.

Приведение дневной или месячной доходности к годовой

Если вы располагаете среднедневной или среднемесячной доходностью (геометрической), эти данные можно аннуализировать по таким формулам:

• для дневной доходности: (x + 1) ^ 252 — 1, где x – доходность в процентах и 252 — число торговых дней в году;
• для месячной доходности: (x + 1) ^ 12 — 1.

Например, приведение дневной доходности 0,03% может выглядеть так: (0,0003 + 1) ^ 252 — 1 = 7,9%. Естественно, то же самое можно делать для недельной или квартальной доходности (возводя в 52 или 4 степень).

При этом аннуализированное СКО рассчитывается по другой формуле: x * SQRT(252), то есть среднедневную волатильность нужно умножить на квадратный корень из количества торговых дней (либо месяцев и т. д.).

Расчет годовой доходности с учетом пополнений и изъятий (движения средств)

Все вышеперечисленные способы подходят для расчета доходности активов или экономических показателей в вакууме, но личные инвестиции сопряжены с периодическими пополнениями портфеля или изъятиями средств из него.

Если просто рассчитать доходность способами выше, она окажется искаженной этими движениями денег. Например, если на начало года у вас было 100 000 руб., потом вы купили активы на 80 000 руб., а в конце года стоимость портфеля составила 200 000 руб., это не значит, что вы заработали 200000 / 100000 — 1 = 100%.

В таких случаях есть несколько способов посчитать свой финансовый результат, устранив движения средств из показателя доходности. Наиболее удобный из них – это расчет внутренней нормы (или ставки) доходности (internal rate of return, IRR), потому что для этого есть две функции в Excel.

1. ВСД (IRR) – для регулярных во времени пополнений или изъятий (например, каждый месяц, квартал или год);
2. ЧИСТВНДОХ (XIRR) – для нерегулярных, что и применяется в реальной жизни.

Всё, что нужно сделать, это передать в функцию ЧИСТВНДОХ диапазоны ячеек с суммами и датами, при этом пополнения будут положительными числами, а изъятия отрицательными (или наоборот), а последней должна быть текущая стоимость портфеля, как если бы вы сняли всё в последний день. Если те 80 000 руб. мы положили 6 июля, то для нашего примера это будет выглядеть так:

• 2019-01-01: -100000
• 2019-07-06: -80000
• 2019-12-31: 200000

Годовая доходность: ЧИСТВНДОХ(B1:B3; A1:A3) = 14,56%.

В колонке A были даты, в B – суммы.

Расчет стандартного отклонения

В любых электронных таблицах рассчитать стандартное отклонение не составляет труда. Его можно считать для годовых или любых других доходностей, выраженных в процентах или разах, приводить месячное стандартное отклонение к годовому и так далее. Стандартное отклонение также называется среднеквадратическим или СКО.

Для этого нам понадобится функция СТАНДОТКЛОН (STDEV), куда достаточно просто передать диапазон ячеек с доходностями. Она рассчитывает СКО для выборки из генеральной совокупности, что нам и нужно.

Если взять пример с инфляцией в России за последние 5 лет, получим такой результат:

СТАНДОТКЛОН(11,35%; 12,91%; 5,39%; 5,39%; 4,26%) = 3.96%.

Источник