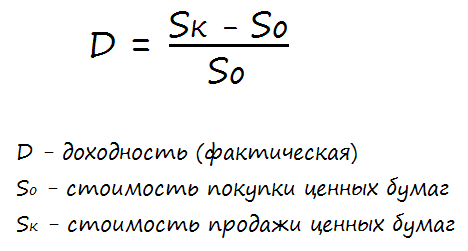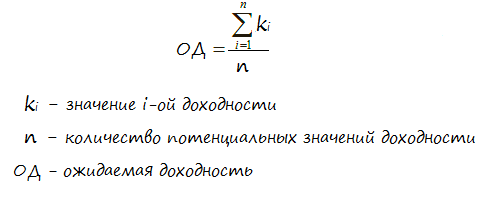Как оценить вероятность того что доходность

Доходность ценных бумаг. Основные методы оценки и прогнозирования

Ни для кого не секрет, что основной целью инвестиций в ценные бумаги является получение максимально возможной прибыли при сохранении приемлемого уровня риска. В этой статье я расскажу вам о том, какие виды ценных бумаг обладают потенциально большим потенциалом доходности. Вы узнаете о том из чего складывается их доходность и каким образом она вычисляется. Наконец, мы с вами подробно поговорим о том, как можно провести предварительную оценку и рассчитать ожидаемую доходность ценных бумаг ещё на этапе их выбора.

Какие бумаги потенциально самые прибыльные

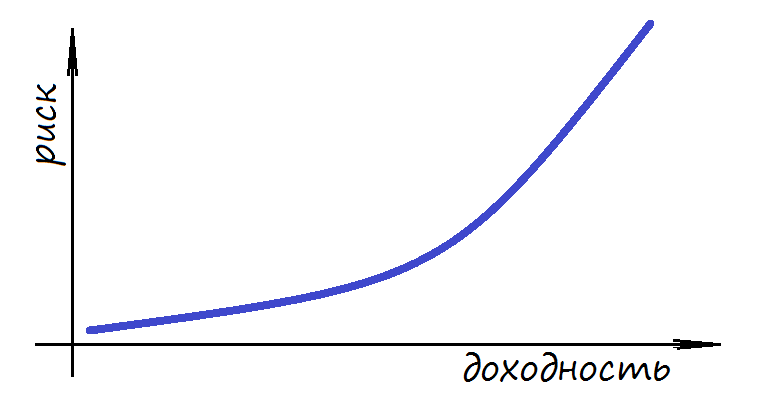
Ответ на этот вопрос довольно прост: самый большой потенциал в плане прибыли имеют ценные бумаги с таким же большим уровнем риска. Чем выше риск, который готов взять на себя инвестор, тем выше тот доход, который он может в итоге получить. Ключевое слово в данном случае – «может», поскольку с увеличением степени риска вероятность получения дохода постепенно тает.

Соотношение риска и доходности

То есть, другими словами, увеличивая степень риска инвестор одновременно и повышает свою потенциальную доходность, и снижает вероятность её получения. Поэтому в инвестициях так важно найти ту самую золотую середину, тот уровень риска при котором можно рассчитывать на относительно высокую прибыль с достаточно большой вероятностью её получения.

Минимальным риском, но и наименьшей степенью доходности отличаются такие бумаги, как государственные облигации. Обычно процент по ним сопоставим с доходностью банковских депозитов и едва превышает текущий уровень инфляции. Инвестирование в бумаги данного типа целесообразно в тех случаях, когда основной целью является не приумножение, а сохранение своих денежных средств.

На ступеньку выше стоят корпоративные облигации крупнейших компаний. Они также обладают достаточной степенью надёжности, но позволяют получить чуть большую прибыль (в отличие от бумаг выпущенных государством). Ещё выше по доходности – акции тех же самых компаний, но и риск по ним тоже чуть выше. Облигация по природе своей — долговая ценная бумага, то есть она подразумевает возврат долга и процентов по нему в любом случае. А вот акция — бумага долевая. Она даёт своему владельцу долю в бизнесе компании её выпустившей, но вместе с этим он принимает на себя и определённые риски (в частности, убытки в результате возможного снижения курса акций).

Ещё более рисковыми, но и потенциально более доходными являются акции и облигации выпущенные не столь известными и не столь крупными компаниями. При этом, чем менее известна компания, тем большую прибыль она вынуждена обещать по своим облигациям (иначе никто не захочет их покупать) и тем сильнее могут в итоге «выстрелить» её акции. Ведь согласитесь, что у автосервиса за углом вашего дома, потенциал к возможному росту куда выше чем, например, у Газпрома или Сбербанка. Автосервис может увеличиться в тысячи раз развивая свой бизнес в сеть по всему городу, по всей стране или, в конце концов, даже по всему миру (вовсе не обязательно что он это сделает, но, тем не менее, теоретическая возможность этого ведь существует). А вот Газпром это уже и так достаточно крупная организация и вряд ли он сможет увеличить свою рыночную капитализацию даже в 5-10 раз.

Есть ещё такие бумаги как фьючерсные и опционные контракты. Торговля ими осуществляется с использованием кредитного плеча (левериджа) и, соответственно, размер потенциальной прибыли в данном случае гораздо выше, он прямо пропорционален размеру предоставляемого плеча. Аналогичным образом растёт и риск.

Предположим, что вы решили приобрести фьючерс на акции IBM. Спецификация данного фьючерсного контракта подразумевает его торговлю с размером левериджа 1 к 10. То есть, при цене одной акции в 135 долларов, обладая суммой в 1350$, вы можете приобрести не десять, а сто таких акций. Хотя если говорить точнее, в данном случае вы приобретёте не сами акции IBM, а фьючерсный контракт на их покупку. Но сути дела это сильно не меняет, ведь по истечении срока данного контракта вы сможете получить прибыль равнозначную той, которая была бы у вас при продаже этих самых акций. Правда при этом и возможный убыток будет равен тому, который вам принесло бы обладание 100 акциями IBM в случае снижения их курсовой стоимости.

Формулы расчёта доходности ценных бумаг

Вообще, доходность по ценным бумагам может складываться из следующих величин:

1. Спекулятивный доход получаемый в результате реализации курсовой разницы при покупке и продаже ценных бумаг;
2. Доход получаемый в виде дивидендов по акциям или в виде процентов по облигациям (купонный доход).

Кроме этого можно говорить о фактической и ожидаемой доходности инвестиций. Фактическая доходность отражает ту величину прибыли, которая была получена, что называется, постфактум. А ожидаемая — показывает ту её величину, которую можно будет получить в будущем.

Про ожидаемую доходность мы поговорим в следующем разделе, а сейчас давайте рассмотрим как рассчитывается фактическая доходность инвестиций в ценные бумаги.

Если речь идёт о чисто спекулятивной доходности (от разницы курсовой стоимости), то её легко можно рассчитать по формуле:

В том случае, если помимо курсовой разницы были получены ещё проценты или дивиденды, доход рассчитывается по формуле:

Обычно доходность рассчитывается в процентах годовых. Для того чтобы привести рассчитанные по вышеприведённым формулам результаты к годовой доходности, следует воспользоваться этой зависимостью:

Ожидаемая доходность ценных бумаг

Грамотное инвестирование в ценные бумаги, предполагает вероятностную оценку рисков и возможностей, выбор допускаемого значения риска и сопоставимого с ним потенциального уровня доходности**. Об инвестиционных рисках и о способах их минимизации мы говорили с вами здесь. А сейчас я расскажу вам о том, как оценить потенциальную доходность ценных бумаг.

Оценить ожидаемую доходность (ОД) можно двумя различными методами. Первый метод основан на вероятностях (математическом ожидании), а второй — на исторических данных. Давайте начнём с вероятностного метода оценки.

** Как мы уже говорили с вами выше, риск и доходность ценных бумаг находятся в прямо пропорциональной зависимости друг от друга. Чем выше риск, тем выше потенциальный уровень доходности и наоборот. Такое положение вещей обусловлено тем, что рынок сам устанавливает данное соотношение, ведь никто не хочет покупать высокорисковые бумаги с небольшим уровнем доходности.

Оценка доходности на основе математического ожидания

В данном случае учитываются все возможные варианты размера предполагаемой доходности вкупе с их вероятностью. Причём наибольший вес придаётся тем значениям, вероятность получения которых выше.

Расчёт производится по формуле:

Для наглядности вычислений, давайте приведём простой пример. Допустим перед инвестором встал выбор из двух бумаг со следующим распределением вероятностей прибылей по ним:

1. Бумага А предположительно принесёт доходность в 10% с вероятностью в 50%, доходность в 7% с вероятностью в 30% или доходность в 4% с вероятностью в 20%;
2. Бумага Б. Вероятность доходности в 12% составляет 30%, вероятность доходности в 8% составляет 35% и вероятность доходности в 5% составляет 35%.

Сначала рассчитываем ожидаемую доходность для бумаги А:

ОД = (0,1*0,5) + (0,07*0,3) + (0,04*0,2) = 0,079 = 7,9%

А теперь рассчитаем ожидаемую доходность для бумаги Б:

ОД = (0,12*0,3) + (0,08*0,35) + (0,05*0,35) = 0,081 = 8,1%

Очевидно, что фактическое значение доходности, скорее всего, будет несколько отличаться от рассчитанного по вышеприведённой формуле. Оценить разброс значений фактических, относительно значений расчётных, можно рассчитав величину дисперсии.

Дисперсия рассчитывается по формуле:

Для нашего примера получим дисперсию для бумаги А:

0,5(0,1 — 0,079) 2 + 0,3(0,07 — 0,079) 2 + 0,2(0,04 — 0,079) 2 = 0,000549

И дисперсию для бумаги Б:

0,3(0,12 — 0,081) 2 + 0,35(0,08 — 0,081) 2 + 0,35(0,05 — 0,081) 2 = 0,000793

Дисперсия показывает тот уровень риска, который повлечёт за собой инвестирование в бумагу для которой была рассчитана ожидаемая доходность на основе вероятностей (математического ожидания). Чем больше дисперсия, тем больше возможное отклонение фактического значения ОД от расчётного.

В нашем примере дисперсия для бумаги Б несколько выше аналогичного показателя для бумаги А. Однако, разница между ними совсем незначительная (не на порядок), поэтому можно считать, что риски рассматриваемых бумаг примерно равны. Следовательно, при прочих равных, инвестирование в бумагу Б является предпочтительным.

Оценка доходности на основе исторических данных

Как вы понимаете, не всегда есть возможность объективно оценить вероятности получения того или иного размера прибыли. Поэтому, на практике часто используют второй метод оценки ОД. Для второго способа расчёта ОД предполагается наличие данных по доходности за несколько равных временных периодов (например, за несколько лет).

Расчёт производится по следующей формуле:

Для примера, давайте опять сравним акции двух компаний А и Б. Для простоты примера возьмём статистику годовой доходности за три последних года. Пускай акции компании А приносили доход в размере:

1. Первый год — 10%;
2. Второй год — 8%;
3. Трети год — 15%.

А акции компании Б:

1. Первый год — 5%;
2. Второй год — 15%;
3. Третий год — 10%.

Подставляя эти значения в формулу получим, для акций компании А:

Для акций компании Б:

Как видите, согласно расчёту, акции компании Б оказываются чуть более выгодными. Однако следует иметь ввиду, что значения доходности в прошлом, не гарантируют её в будущем. Так, в данном примере, на третий год произошло некоторое снижение прибыли. Это может быть вызвано как временными, но преодолимыми трудностями (вызванными, например, изменением конъюнктуры на рынках сбыта), так и свидетельствовать о более серьёзных проблемах компании (наличие которых, скорее всего, повлечёт за собой дальнейшее снижение прибыльности её бумаг).

Источник

CFA — Как оценивать вероятность событий при принятии финансовых решений?

Рассмотрим основные вероятностные инструменты, необходимые финансовому аналитику для прогнозирования и решения многих реальных проблем, связанных с риском, — в рамках изучения количественных методов по программе CFA.

Все инвестиционные решения принимаются в условиях риска. Инструменты, которые позволяют нам принимать решения последовательно и логично в этой ситуации, относятся к категории вероятностных. В этом чтении представлены основные вероятностные инструменты, необходимые для решения многих реальных проблем, связанных с риском.

Мы покажем, как эти инструменты применяются к решению таких вопросов, как прогнозирование эффективности работы инвестиционного управляющего, прогнозирование финансовых показателей и ценообразование облигаций таким образом, чтобы они справедливо компенсировали своим держателям риск дефолта.

При этом мы сфокусируемся на практических аспектах: подробно исследуем концепции, которые наиболее важны для инвестиционных исследований и практики.

Одной из таких концепций является независимость событий, поскольку она связана с предсказуемостью доходов и финансовых показателей. Другая — ожидание, так как аналитики постоянно смотрят в будущее в своих анализах и решениях.

Аналитики и инвесторы также должны справляться с изменчивостью. Здесь мы рассмотрим дисперсию или изменчивость ожиданий как концепцию риска, важную для инвестиций.

В этом разделе рассматриваются:

• Основные инструменты вероятности, в том числе математическое ожидание и дисперсия.
• Ковариация и корреляция (показатели взаимосвязи между случайными величинами) и принципы расчета ожидаемой доходности и дисперсии портфеля.
• Формула Байеса и подсчет результатов.

Формула Байеса — это процедура обновления (корректировки) убеждений на основе новой информации. В нескольких областях, включая широко используемую биномиальную модель ценообразования опционов, расчет вероятностей включает в себя определение и подсчет результатов.

Что такое вероятность события?

Вероятностные концепции и инструменты, необходимые для большей части работы финансового аналитика, относительно немногочисленны и просты, но требуют обдуманного применения.

В этом разделе представлены основы работы с вероятностью, ожиданиемым значением и дисперсией, — на примерах анализа рынка капитала и инструментов с фиксированным доходом.

Внимание инвестора сфокусировано на доходности. Доходность рискованного актива является примером случайной величины (англ. ‘random variable’), то есть величины, результаты (возможные значения) которой являются неопределенными.

Например, портфель может иметь целевую доходность 10% годовых. На данный момент портфельный менеджер может сосредоточиться на вероятности получения прибыли, которая в следующем году составит менее 10%.

10 процентов — это конкретное значение или результат случайной величины «доходность портфеля». Хотя мы можем быть обеспокоены одним результатом, часто наш интерес может быть связан с рядом результатов: понятие «событие» охватывает оба варианта.

Определение события.

Событие (англ. ‘event’) — это определенный набор результатов или исходов (англ. ‘outcomes’).

Мы можем определить событие как единый результат — например, портфель приносит доход 10% (курсивом выделено определение события).

Мы также можем отразить озабоченность менеджера портфеля, определив событие следующим образом: портфель приносит доход ниже 10%.

Это второе событие, относящееся ко всем возможным доходам, которые ≥ -100% (наихудший возможный доход), но

Насколько вероятно, что портфель получит доход ниже 10%?

Ответ на этот вопрос — вероятность (англ. ‘probability’): число от 0 до 1, которое измеряет вероятность того, что указанное событие произойдет. Если вероятность того, что портфель принесет доход ниже 10% составляет 0.40, это означает, что вероятность этого события составляет 40%.

• Если событие невозможно, оно имеет вероятность 0.
• Если событие обязательно произойдет, оно имеет вероятность 1.
• Если событие невозможно или произойдет в любом случае, оно вовсе не случайно.
• Диапазон от 0 до 1 включает все возможные значения вероятности.

Вероятность имеет два свойства, которые вместе составляют ее определение.

Определение вероятности.

Два определяющих свойства вероятности таковы:

1. Вероятность любого события E представляет собой число от 0 до 1: 0 ≤ P(E) ≤ 1.
2. Сумма вероятностей любого набора взаимоисключающих и исчерпывающих событий равна 1.

P с последующими круглыми скобками означает «вероятность (событие в скобках)», то есть P(E) — это «вероятность события E». Мы также можем думать о P как о правиле или функции, которая присваивает числовые значения событиям, соответствующим указанным выше свойствам 1 и 2.

В приведенном выше определении термин взаимоисключающий (англ. ‘mutually exclusive’) означает, что одновременно может происходить только одно событие; термин исчерпывающий (англ. ‘exhaustive’) означает, что события охватывают все возможные результаты.

События A = портфель с доходностью 10% и B = портфель с доходностью ниже 10% являются взаимоисключающими, поскольку A и B не могут происходить одновременно.

Например, доходность 8.1% означает, что событие B произошло, а событие A не произошло. Хотя события A и B являются взаимоисключающими, они не являются исчерпывающими, поскольку они не охватывают такие результаты, как доходность в 11%.

Предположим, мы определили третье событие: C = портфель приносит доход выше 10%.

Очевидно, что A, B и C являются взаимоисключающими и исчерпывающими событиями. Каждое из событий P(A), P(B) и P(C) является числом от 0 до 1, и
P(A) + P(B) + P(C) = 1.

Самым основным видом взаимоисключающих и исчерпывающих событий является набор всех различных возможных результатов случайной величины. Если мы знаем и этот набор, и распределение вероятностей для этих результатов (распределение вероятностей случайной величины) — у нас есть полное описание случайной величины, и мы можем назначить вероятность любому событию, которое мы можем описать.

В чтении об общих распределениях вероятностей мы опишем некоторые из распределений вероятностей, наиболее часто используемых в инвестиционной практике.

Вероятность любого события — это сумма вероятностей различных результатов, включенных в определение события.

Предположим, что интересующим событием является D = портфель приносит доход выше безрисковой ставки, и мы знаем распределение вероятностей доходности портфеля.

Предположим, безрисковая ставка составляет 4%. Чтобы вычислить P(D), т.е. вероятность события D, мы суммируем вероятности результатов, которые удовлетворяют определению события; то есть мы суммируем вероятности доходности портфеля более 4%.

Ранее, чтобы проиллюстрировать концепцию, мы предполагали вероятность 0.40 для портфеля с доходностью менее 10%, без обоснования конкретного предположения. Мы также говорили об использовании распределения вероятностей результатов для вычисления вероятности событий, не объясняя, как можно получить распределение вероятностей.

Принятие фактических финансовых решений с использованием неточных вероятностей может иметь серьезные последствия.

Как на практике мы оцениваем вероятность события?

Эта тема сама по себе является предметом изучения, но существует 3 основных подхода к оценке вероятностей.

1. В инвестициях мы часто оцениваем вероятность события как относительную частоту его возникновения, основываясь на исторических данных. Этот метод позволяет найти эмпирическую вероятность (англ. ’empirical probability’).

Например, Thanatawee (2013) сообщает, что в его выборке из 1927 ежегодных наблюдений за нефинансовыми фирмами SET (Фондовая биржа Таиланда) в период с 2002 по 2010 год 1382 были фирмами, выплачивающими дивиденды, и 545 были компаниями, не выплачивающими дивиденды. Таким образом, эмпирическая вероятность того, что тайская фирма выплатит дивиденды, составляет приблизительно 1 382/1 927 = 0,72.

2. Результаты должны стабильно прослеживаться с течением времени, чтобы эмпирические вероятности были точными. Мы не можем рассчитать эмпирическую вероятность события, отсутствующего в исторической записи, или достоверную эмпирическую вероятность очень редкого события.

Таким образом, существуют случаи, когда мы можем скорректировать эмпирическую вероятность, чтобы учесть восприятие меняющихся результатов.

3. В других случаях у нас вообще нет возможности использовать эмпирическую вероятность. Поэтому мы также можем сделать личную оценку вероятности без ссылки на какие-либо конкретные данные.

Каждый из этих трех типов вероятности является субъективной вероятностью (англ. ‘subjective probability’), основанной на личном или субъективном суждении.

Субъективные вероятности имеют большое значение в инвестициях. Инвесторы, принимая решения о покупке и продаже, которые определяют цены активов, часто опираются на субъективные вероятности.

Субъективные вероятности появляются в разных местах в этом чтении, особенно в обсуждении формулы Байеса.

В более узком диапазоне четко определенных проблем мы иногда можем вывести вероятности, рассуждая о проблеме. Результирующая вероятность — это априорная вероятность (англ. ‘a priori probability’), основанная на логическом анализе, а не на наблюдении или личном суждении.

Мы будем использовать этот тип вероятности в приведенном далее, в Примере (6).

Методы подсчета, которые мы обсудим позже, особенно важны при вычислении априорной вероятности.

Поскольку априорные и эмпирические вероятности обычно не зависят от конкретного человека, они часто группируются как объективные вероятности.

Источник