Коэффициент корреляции | Correlation coefficient
В статистике коэффициент корреляции (англ. Correlation Coefficient) используется для проверки гипотезы о существовании зависимости между двумя случайными величинами, а также позволяет оценить ее силу. В портфельной теории этот показатель, как правило, используется для определения характера и силы зависимости между доходностью ценной бумаги (актива) и доходностью портфеля. Если распределение этих переменных является нормальным или близким к нормальному, то следует использовать коэффициент корреляции Пирсона, который рассчитывается по следующей формуле:
— среднеквадратическое (стандартное) отклонение доходности i-ой ценной бумаги;
— среднеквадратическое (стандартное) отклонение доходности портфеля.
В расширенном виде формулу коэффициента корреляции Пирсона можно записать следующим образом:
где ki – доходность ценной бумаги в i-ом периоде;
— ожидаемая (средняя) доходность ценной бумаги;
pi – доходность портфеля в i-ом периоде;
— ожидаемая (средняя) доходность портфеля.
n – количество наблюдений.
Свойства коэффициента корреляции
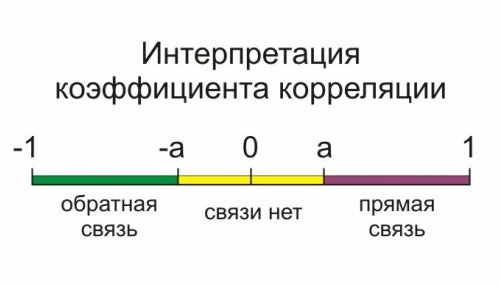
Значение коэффициента корреляции изменяется от -1 до +1. Его отрицательное значение говорит о том, что между переменными наблюдается обратная взаимосвязь. Например, когда доходность ценной бумаги будет расти, то доходность портфеля будет падать, и наоборот. Положительное значение свидетельствует о прямой взаимосвязи, то есть, если доходность ценной бумаги будет расти, доходность портфеля также будет расти, и наоборот.
Если абсолютное значение коэффициента корреляции находится ближе к 1, то это свидетельствует о сильной взаимосвязи между переменными, а если ближе к 0 — то это говорит о слабой связи или ее отсутствии. Если его значение равно -1 или +1, то можно говорить о существовании функциональной взаимосвязи между переменными, то есть одну из них можно выразить через другую посредством математической функции.
Пример расчета
Динамика доходности акций Компании А и Компании Б, а также динамика доходности портфеля ценных бумаг выглядят следующим образом:
Чтобы использовать формулу коэффициента корреляции Пирсона необходимо рассчитать среднюю доходность, которая составит:
- для акций Компании А 4,986%;
- для акций Компании Б 5,031%;
- для портфеля 3,201%.
Ковариация доходности акций Компании А и портфеля составит -0,313, а акций Компании Б и портфеля 0,242. (О том, как рассчитывается ковариация доходности можно прочитать здесь)
Среднеквадратическое отклонение доходности акций Компании А составит 0,6398, акций Компании Б 0,5241 и портфеля 0,5668. (О том, как рассчитывается среднеквадратическое отклонение можно прочитать здесь)
Коэффициент корреляции доходности акций Компании А и доходности портфеля составит -0,864, а акций Компании Б 0,816.
RБ = 0,242/(0,5241*0,5668) = 0,816
Можно сделать вывод о присутствии достаточно сильной взаимосвязи между доходностью портфеля и доходностью акций Компании А и Компании Б. При этом, доходность акций Компании А демонстрирует разнонаправленное движение с доходностью портфеля, а доходность акций Компании Б однонаправленное движение.
Источник
Asset Allocation: корреляция активов
Автор: Алексей Мартынов · Опубликовано 23.05.2016 · Обновлено 22.08.2016
В предыдущей статье мы говорили, что ребалансировка активов контролирует риск портфеля, а при удачном стечении обстоятельств может дать дополнительный выигрыш по доходности. Но это работает только в том случае, если активы в портфеле ведут себя по разному в одних и тех же условиях. Как найти такие активы, и как оценить их поведение между собой, вы узнаете из этой статьи.
В портфель должны включаться слабо взаимосвязанные активы, цена которых ведет себя по разному в одинаковых условиях. Это снижает риск портфеля и создает портфельный эффект. Связь разных активов между собой можно оценить математически с помощью корреляции. Корреляция показывает в какой степени динамика стоимости одного актива соотносится с динамикой другого актива.
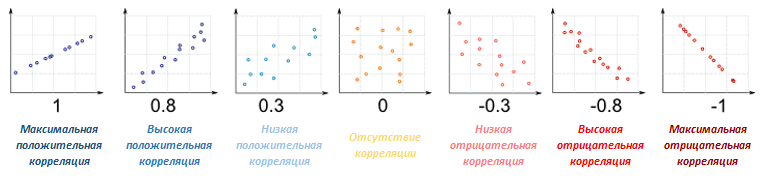
Корреляция может принимать значения от +1 (положительная) до -1 (отрицательная). Если цены активов движутся в одном направлении (оба растут или оба снижаются), корреляция положительна (больше 0), если цены активов движутся в противоположных направлениях (один растет, второй снижается), корреляция отрицательная (меньше 0).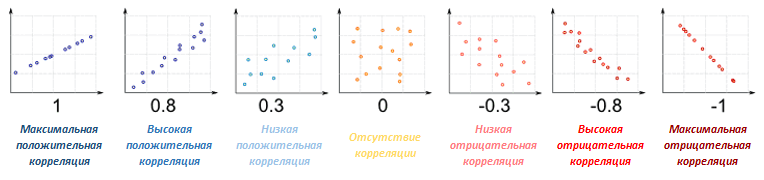 
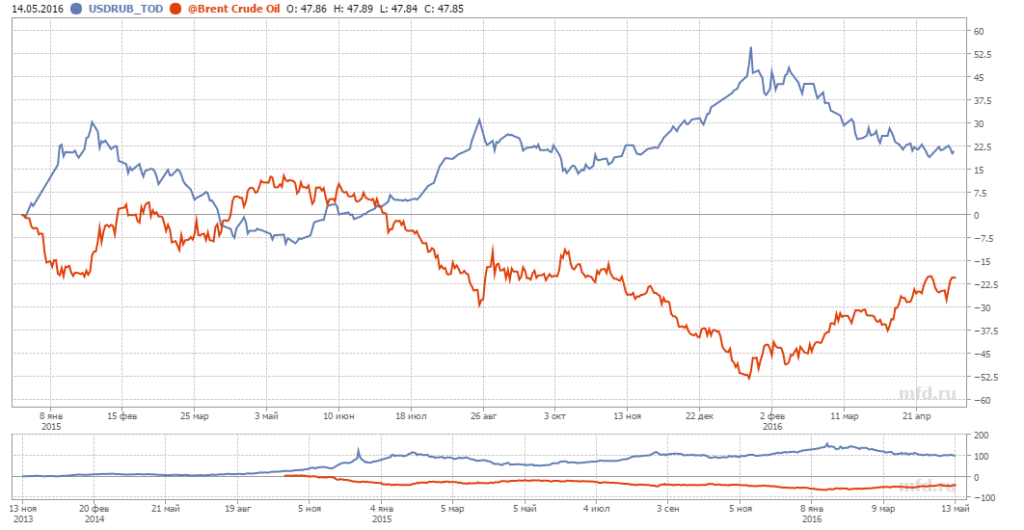
Корреляция равная +1 означает, что стоимость активов меняются идентично друг другу: если один актив вырос на 10%, второй тоже растет на 10%. Корреляция равная -1 означает, что цены движутся максимально противоположно. Нулевая корреляция означает, что взаимосвязи нет.
Из реальной жизни пример негативной корреляции можно найти в динамике курса доллара и цен на нефть в 2015-16 годах: когда нефть падала, курс доллара рос.
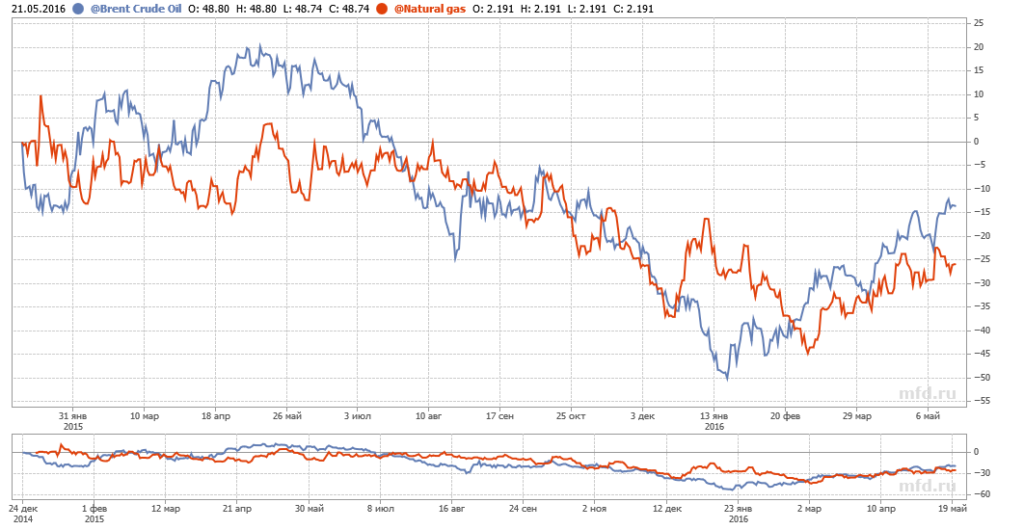
Положительная корреляция есть между ценами на нефть и натуральный газ: их цены двигаются схожим образом.
Влияние корреляции на риск портфеля
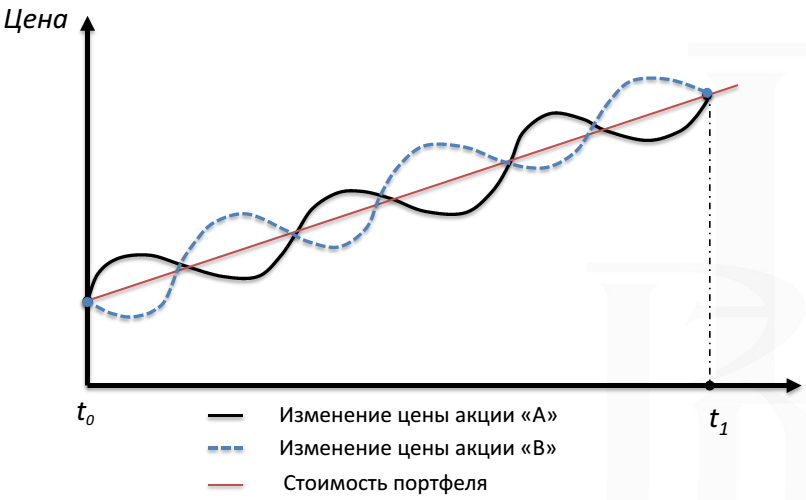
Поведение активов влияет на риск портфеля. Например, на картинке ниже изображены две акции, стоимость которых изменяется противоположно: когда одна растет, другая падает. Корреляция таких акций будет отрицательной. Если портфель будет состоять поровну их этих акций, то его стоимость будет изменяться гораздо плавнее по сравнению с каждой акцией в отдельности, то есть риск портфеля будет ниже, чем риск составляющих его акций. Это конечно идеализированная модель, но она наглядно показывает, как отрицательная корреляция активов снижает риск портфеля.
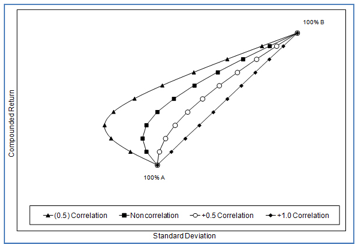
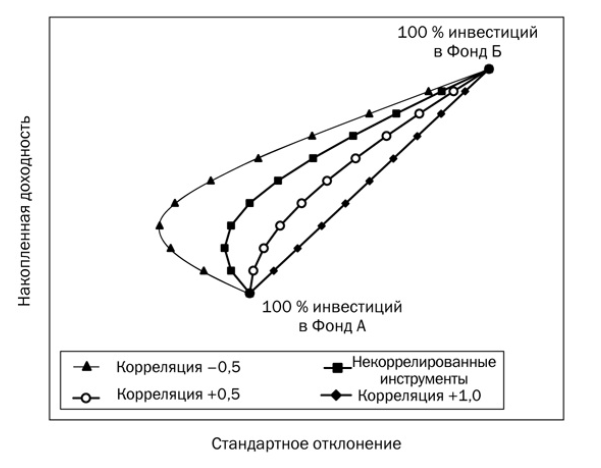
Теперь посмотрим, как корреляция может влиять на риск и доходность портфеля. На графике ниже изображена так называемая граница эффективности портфеля, состоящего из двух активов — А и В. Вертикальная ось — доходность портфеля, горизонтальная ось — стандартное отклонение доходности. Каждая линия представляет собой портфель с разной степенью корреляции активов (-0.5, 0.0, +0.5 и +1.0). Каждая точка на линии — это разные пропорции активов в портфеле, начиная от 100% А, далее 90% А:10% В и так далее до 100% В.
Источник: Richard Ferri, Portfolio Solutions
Нетрудно заметить, что портфели активов с отрицательной корреляцией -0,5 находятся в левой части диаграммы и имеют самое низкое стандартное отклонение доходности, то есть самый низкий риск среди всех рассматриваемых портфелей. А портфели активов с высокой корреляцией имеют самый высокий риск. Таким образом при прочих равных риск портфеля снижается когда активы имеют низкую корреляцию.
Корреляция активов
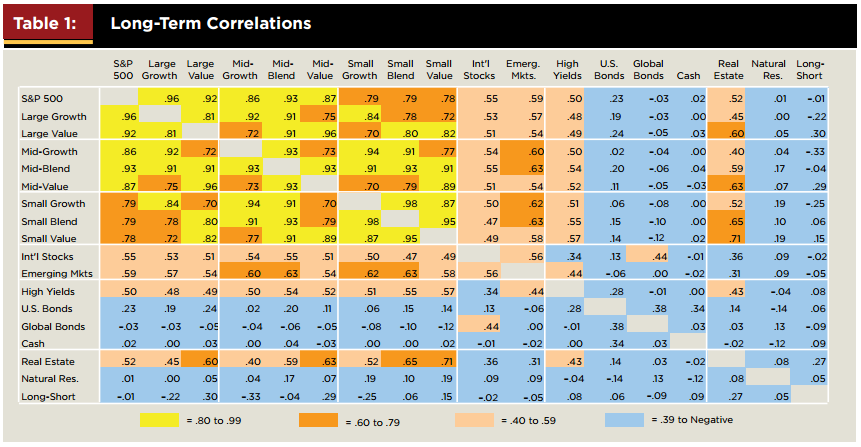
К сожалению, в реальной жизни довольно трудно найти два актива с абсолютно нулевой или отрицательной корреляцией. Большинство активов имеют корреляцию где-то между 0 и+1. В таблице 1 представлена матрица корреляции между разными классами активов с 1970 по 2004 год. Чем холоднее цвет, тем ниже корреляция. Можно заметить, что холодные цвета присутствуют в основном у облигаций, кэша и ресурсов. Эти классы активов хуже всего коррелируют с акциями различной капитализации и недвижимостью. Однако даже среди них редко встречаются отрицательные значения.
Источник: Journal of financial planning
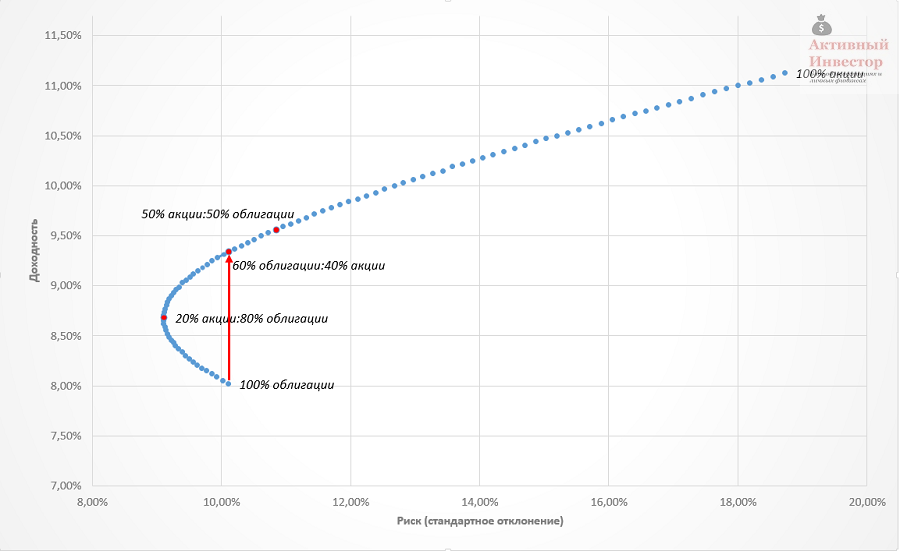
Если взять реальный пример, то корреляция между американскими акциями и долгосрочными государственными облигациями на сроке 1972-2015 составила 0,01, то есть фактически отсутствовала. Граница эффективности портфеля, состоящего их этих двух классов активов очень похожа на линию на графике выше, которая соответствует портфелю из некоррелируемых активов.
Низкая корреляция между активами создает портфельный эффект — когда по характеристикам риск и доходность портфеля может быть лучше активов, из которых он состоит. Логично было бы ожидать, что самый низкий риск будет иметь портфель, состоящий полностью из облигаций. Но в реальности самым низким риском обладает портфель, доля облигаций в котором 80%, а на акции приходится 20%. Добавление акций не только уменьшило риск портфеля, но и увеличило его доходность на 0,6%. Другой портфель 60:40 показал такой же риск, как и 100% облигаций, но его доходность при этом была почти на 1,5% больше.
Корреляция непостоянна
Ричард Ферри в своей статье в журнале Forbes обратил внимание, что, к сожалению, теория, которая красиво выглядит на длительном сроке, не всегда хорошо работает на коротких периодах. Например, с 1926 по 2013 год корреляция между акциями США и 5-летними казначейскими облигациями была равна 0,07. Это очень низкая корреляция для двух классов активов, значит эти два класса активов в портфеле должны хорошо работать вместе.
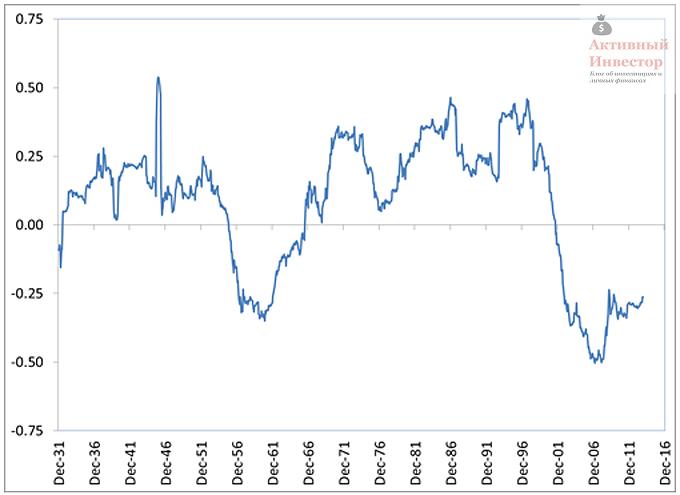
К сожалению, долговременная корреляция не отражает то, что происходит в течение коротких периодов. На графике ниже показано, как сильно может меняться корреляция на коротком сроке. На рисунке изображена 5-ти летняя скользящая корреляция между американскими акциями и 5-летними облигациями, рассчитанная на отрезке 1926-2013.
Источник: Richard Ferri, Portfolio Solutions
Пятилетняя корреляция колебалась в диапазоне от -0,5 до +0,5 и лишь изредка равнялась долгосрочной. Это означает, что какую-то часть времени стоимость активов менялась схожим образом, какую-то часть времени — противоположно. Корреляция активов не статична и меняется со временем, иногда очень сильно. Поэтому реализация преимущества низкой корреляции может потребовать длительного времени величиной с десятилетия.
Теперь возьмем и сравним поведение портфеля на двух временных промежутках: с 1970-1985 и с 2002-2013. В период с 1970-1985 корреляция между этими двумя классами активов составляла около +0,3, что привело к доходности портфеля 50:50 всего на 0,5% больше облигаций.
За период с 2002 по 2013 год корреляция между этими двумя классами активов составила около -0,3, в результате чего доходность портфеля превзошла доходность облигаций на 1,7%. Разная корреляция активов может очень сильно менять результаты одного и того же портфеля.
Источник: Richard Ferri, Portfolio Solutions
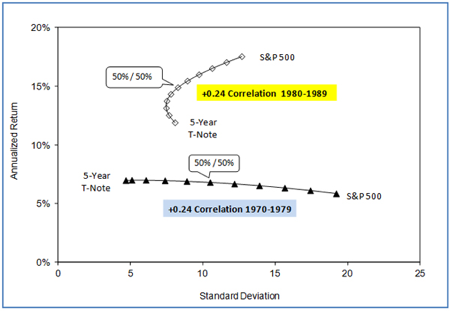
Но даже если корреляция в будущем будет такой же, как она была в прошлом, результаты все равно могут отличаться. Например, 10-летняя корреляция между 5-летними облигациями и акциями США в 70-х годах была +0,24, такой же она была и в 80-х. Но результаты портфелей были различными.
Источник: Richard Ferri, Portfolio Solutions
Низкая корреляция в 70-х годах не дала особых преимуществ: риск портфеля 50/50 оказался выше, а доходность ниже, чем у облигаций. В 80-х аналогичный портфель показал результат гораздо лучше: на 3% больше доходности облигаций при аналогичном риске. Поэтому низкая корреляция двух активов еще не гарантирует уменьшение риска портфеля на коротком сроке.
С течением времени активы с низкой корреляцией находить стало труднее. Финансовые рынки стали более глобальными и взаимосвязанными. Локальный ипотечный кризис 2008 года в США затронул весь мир. Глобализация финансовых рынков сделала так, что инструменты сейчас коррелируют в большей степени, чем раньше. Величина корреляции активов в прошлом зависит от взятого периода и не является надежным индикатором корреляции в будущем.
- Активы, включаемые в портфель, должны иметь низкую положительную или отрицательную корреляцию.
- Низкая корреляция снижает риск портфеля и может увеличить его доходность.
- Долгосрочная корреляция в прошлом — плохой прогнозный индикатор будущей корреляции в краткосрочной перспективе.
- Краткосрочная корреляция — величина непостоянная и может значительно меняться.
- Поэтому для реализации преимущества низкой корреляции требуется длительное время.
- На промежутках времени до 10 лет портфельный эффект может отсутствовать.
Тем не менее это вовсе не означает, что про корреляцию можно совсем забыть. В портфель нужно включать фундаментально разные активы. Высокая положительная корреляция означает отсутствие фундаментальных отличий по риску между активами. Например, высокая положительная корреляция между акциями крупной и средней капитализации будет всегда. Диверсификация по таким активам не принесет большой выгоды портфелю в плане снижения риска. Слабая положительная или отрицательная корреляция служит признаком отличий между активами в плане риска, поэтому включение в портфель активов с низкой положительной или отрицательной корреляцией потенциально уменьшает его риск и создает портфельный эффект, о котором будет написана следующая статья.
Источник
Корреляция активов на финансовых рынках
Что такое корреляция?
Начнем с такого примера. Вы наполняете свой инвестиционный портфель различными инструментами (акциями, облигациями, чем-то еще), но неожиданно замечаете, что в процессе инвестирования все результаты движутся преимущественно в одну сторону. Т.е. вы получаете либо заметную доходность, либо существенный убыток.
Если первая ситуация нас радует, то вторая сильно печалит и мы начинаем задумываться, все ли сделали правильно. И хотя убытки, даже порой затяжные, это неизбежная ситуация реального инвестирования, при составлении нашего портфеля действительно была допущена ошибка, исправление которой поможет заметно улучшить суммарную доходность. Причем решение в данной ситуации представляется достаточно очевидным — портфель должен состоять из активов, которые ведут себя по возможности независимо друг от друга, хотя каждый по отдельности способен быть источником денежного потока.
Корреляция описывается числом в интервале от 1 до -1. Единица со знаком плюс означает абсолютно идентичное движение активов (к такой ситуации, например, близки котировки USD/RUB и EUR/RUB), и в этом случае говорят о полной или максимальной положительной корреляции. Минус один описывает полностью противоположенное поведение, когда рост одного актива всегда вызывает убыток другого — это максимально отрицательная корреляция. Оба варианта скорее идеальные случаи, так что отрицательной корреляцией считается любое негативное значение.
Значение около нуля говорит об отсутствии зависимости между котировками. Т.е. в общем корреляция рассчитывается на основании эмпирических данных — подобная функция есть в Экселе — и поэтому зависит от интервала рассмотрения активов. Корреляция финансовых инструментов имеется как на форекс, так и на фондовом рынке — рассмотрим их отдельно.
Корреляция на рынке форекс
На форекс представлено не такое уж большое число значимых соотношений — семь главных валютных пар уже охватят около 80% валютного рынка. Однако при хаотичном изменении котировок говорить о каком-то постоянном значении коэффициента корреляции валютных пар не приходится — оно полностью зависит от выбранного диапазона. Для иллюстрации этого подойдут две ссылки. Вот первая https://www.home.saxo/insights/tools/fx-correlations-table/tool-details :
Как видно, на настоящий момент тут можно оценить коэффициенты корреляции почти за три года. Причем над таблицей слева находится ползунок, перемещая который можно увидеть, как менялась корреляция валютных пар с периода отсчета (сейчас это 17 ноября 2012) до произвольной даты в течение последнего года. При перемещении этого ползунка будет заметно, что ряд валют не только сильно меняет свое значение, но порой изменяется и сам знак корреляции.
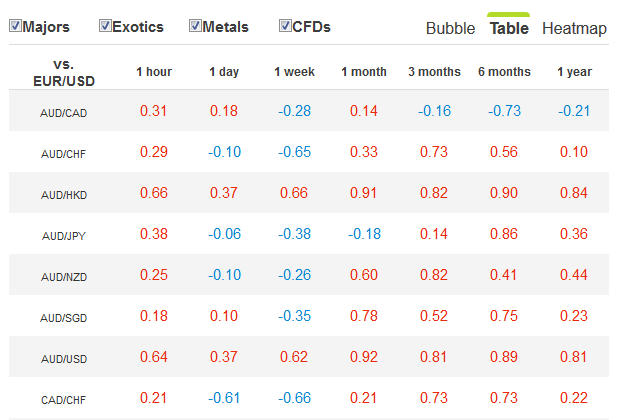
Аналогично можно выбрать периоды за последние 30 и 90 дней — почти наверняка многие показатели в ячейках не будут иметь ничего общего с прежними значениями. Кроме того, очень наглядно корреляция на форекс показана здесь: https://www1.oanda.com/lang/ru/forex-trading/analysis/currency-correlation :
Видно, что в большинстве случаев в течение года валютные пары меняли не только величину, но и знак корреляции к выбранной для сравнения паре (евро/доллар) на противоположенный. Щелчком по другой валютной паре в таблице можно выбрать ее в качестве эталона сравнения.
Корреляция на фондовом рынке
Переходя к фондовому рынку, в первую очередь необходимо обратить внимание на несравненно большее число инструментов, поскольку в принципе каждую акцию (и облигацию) можно рассматривать как отдельный актив. Таблица корреляции каждой акции друг к другу только на американском рынке привела бы к совершенно астрономическим цифрам — слава богу, в распоряжении инвестора есть такой инструмент как ETF, который помогает вложиться в произвольный индекс, отражающий экономику целого государства или даже региона, например Европы.
ETF позволяет широко диверсифицировать капитал — например, биржевой фонд с тикером SPY включает в себя 500 акций компаний США. Но не менее важным является то, что имея простой инструмент для вложения мы можем сравнить индексы различных стран друг с другом (пример — американский S&P500, российский РТС, немецкий DAX и др.) и на выходе получить относительную простую таблицу с достаточно ясными возможностями для инвестирования.
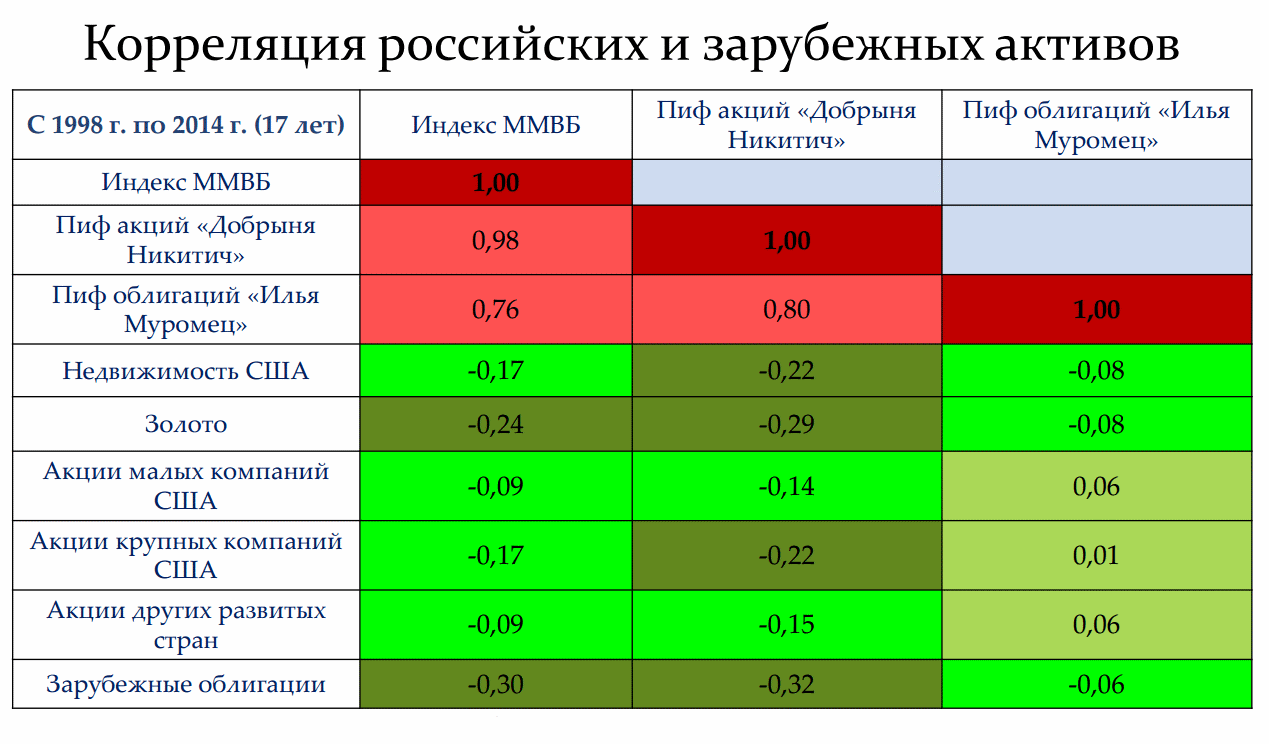
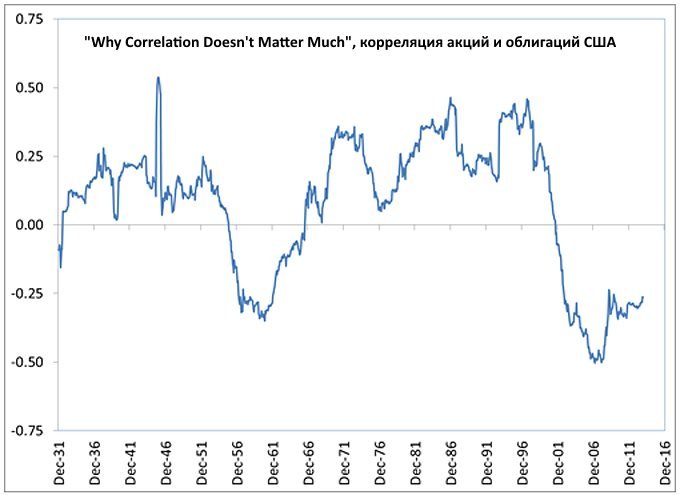
Ложка (и немалая) дегтя в том, что и на фондовом рынке коэффициенты корреляции финансовых инструментов не отличаются постоянством. Однако, в отличие от валютных пар, эти изменения обычно происходят медленнее и находятся в менее широком диапазоне (как будет показано ниже, историческая корреляция американских акций и облигаций с 1930 года описывалась интервалом от +0.5 до -0.5). Рассмотрим корреляцию российских и зарубежных активов (расчеты Сергея Наумова):
Здесь приведена корреляция российских и зарубежных активов на периоде в 17 лет до 2014 года. Из нее видно, что например российские акции и облигации имеют высокую корреляцию друг с другом (их котировки движутся как правило в одном направлении), тогда как золото и зарубежные облигации имели к российским акциям скорее противоположенное движение, т.е. отрицательную корреляцию.
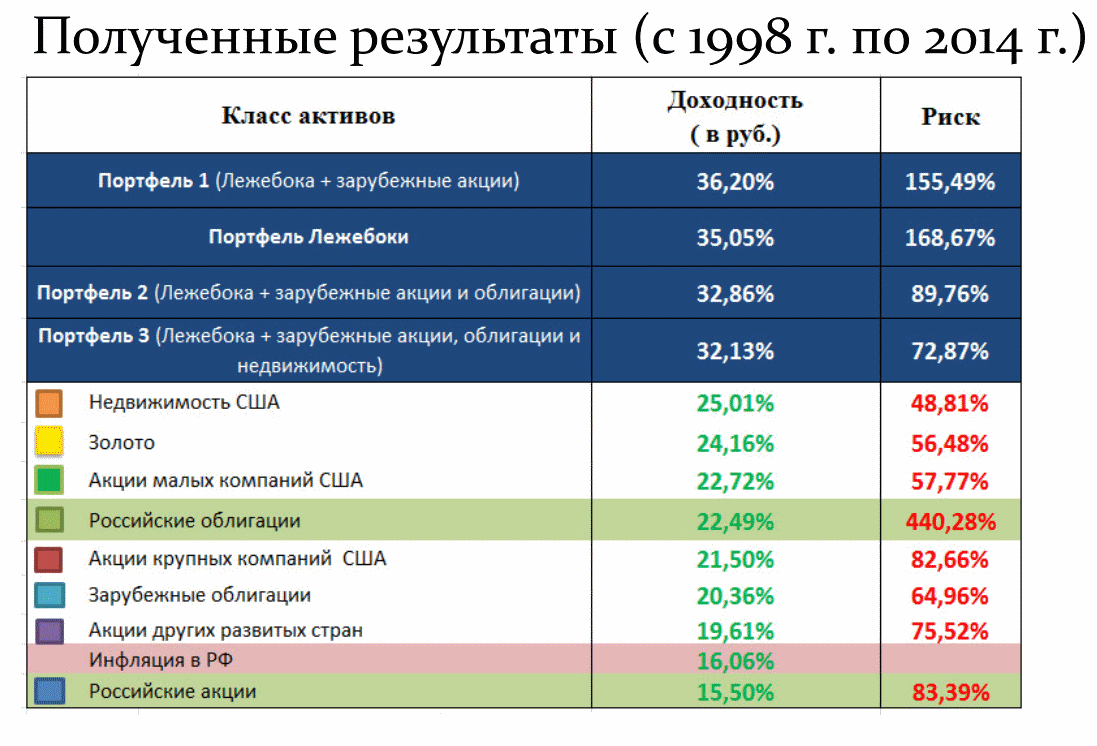
Следовательно, разбавляя американские активы российскими с включением доли золота, можно было бы на первый взгляд добиться сглаживания доходности — однако на практике мы получили бы не просто более ровную кривую, а заметный дополнительный бонус. Посмотрим на таблицу ниже:
Так называемый «портфель лежебоки» — это портфель, включающий равные доли российских акций, облигаций и золота. При этом сравнивая доходность всех четырех портфелей можно увидеть, что она оказалась заметно выше, чем просто арифметическое среднее активов по отдельности! Как такое возможно?
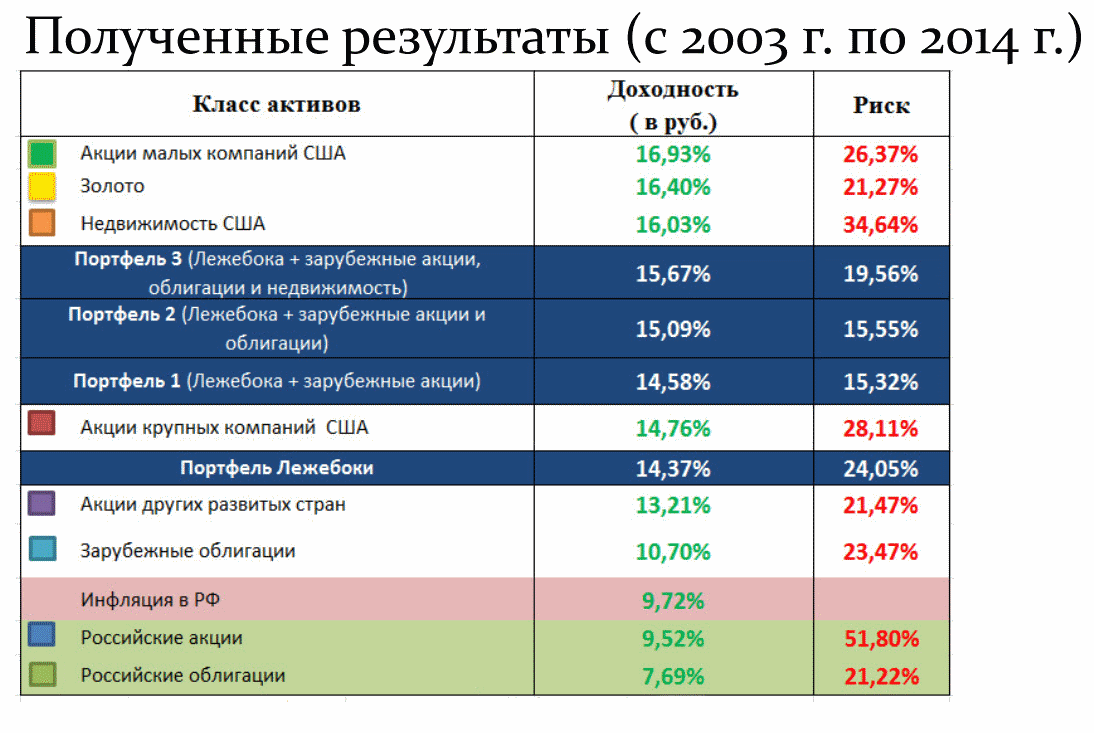
Объяснение этому было дано еще в начале 50-х годов Г. Марковицем, который 30 лет спустя получил за свою теорию Нобелевскую премию — а сама теория стала основой портфельного инвестирования, наряду с понятием о корреляции активов. Согласитесь, что получать в течение 17 лет доходность на уровне 35% в год не позволяет ни один банк — такие предложения делаются лишь откровенными пирамидами. Тем не менее следующий слайд, берущий те же активы, но за другой период, хорошо иллюстрирует высказывание, как прошлая доходность не гарантирует будущей:
Как видно, здесь доходность портфелей представляет уже скорее среднее значение, хотя и лежащее гораздо ближе к верхней границе, чем к нижней; причем риски в этом случае оказываются ниже, чем в прошлой таблице. Откуда такие расхождения? В плане доходности стоит вспомнить огромный рывок российского рынка в 1999 году, когда паи облигаций выросли на невероятные 1800% — и вплоть до 2008 года российский рынок почти непрерывно рос, давая по несколько десятков процентов годовых.
Основной пик пришелся именно на 1999-2000 год. Однако после кризиса 2008 года последовала почти обратная ситуация — несколько восстановившись в 2009 году, в следующие годы даже рублевый индекс ММВБ не сумел достичь своего максимума, а номинированный в долларах РТС и вовсе после декабря 2014 отправился почти к уровню просадки 2008 года. Следовательно, несмотря на отрицательную корреляцию к американскому, российский рынок просто оказался не самым удачным активом, который с 2003 по 2014 годы показал среднюю доходность даже чуть ниже инфляции.
И это является важным фактором, который необходимо учесть — только нулевая или отрицательная корреляция не обеспечит кумулятивный эффект, если хотя бы один из активов будет показывать стагнацию или тем более негативную доходность. Идея именно в том, что в целом доходны оба актива, но проявляется это в разные периоды времени. Поэтому если в качестве развивающегося рынка в дополнение к американскому и европейскому добавлять российские активы, то нужно иметь в виду, что должный эффект, показанный в первой таблице, проявится лишь в случае возобновления роста.
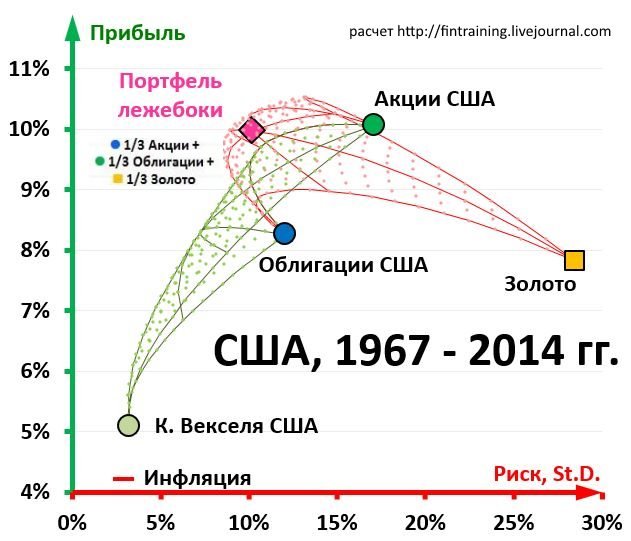
Следовательно, нужно не только учитывать корреляцию, но и в идеальном случае представлять экономические возможности своих активов. При этом на американском рынке аналогичный портфель за почти 50 лет показал те же результаты, что и акции, однако с заметно меньшим риском:
Если же рассмотреть те же данные с 1925 года, то картина немного изменится: хотя доходность по акциям останется почти на том же уровне (9%, т.е. только на 10% меньше), но золото даст результат, близкий к 5% (что меньше почти на 40%). Соответственно, пострадает и портфельный результат: американский «лежебока» с 1925 года даст доходность лишь немногим более 7%, уже заметнее уступая акциям. Поэтому вывод ожидаем: волшебного портфеля нет, а российский лежебока в ближайшие годы скорее всего будет постепенно терять свой громадный отрыв, приближаясь к средним рыночным значениям.
Зависимость корреляции от времени
Как уже упоминалось выше, корреляция не является константой и сама меняется в зависимости от времени. К примеру, корреляция между акциями США и пятилетними гос. облигациями с 1926 по 2013 годы была равна 0.07 — т.е. зависимость почти не прослеживалась. Однако на истории корреляция колебалась от -0,5 до +0,5, причем в XX веке после Великой Депрессии она находилась в отрицательной зоне лишь с середины 50-х по середину 60-х годов. В период с 1970-1985 корреляция акций и облигаций была равна 0.3%, тогда как с 2002-2013 обратной по знаку:
Таким образом, задача поиска доходности зависит от двух неизвестных: корреляции и доходности активов на рассматриваемом промежутке, причем эта доходность достигается с различным риском (отклонением от среднего значения). Отрицательная корреляция в общем случае позволяет достигать большей доходности с меньшим риском по сравнению с менее доходным активом:
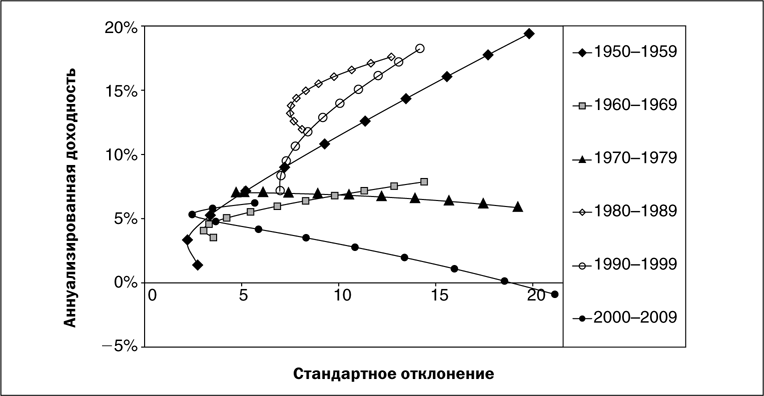
Фонд А — менее волатильный и менее доходный актив (облигации), фонд Б — более волатильный и доходный (акции). Стандартное отклонение определяет размах колебаний относительно среднего значения актива. Такое соотношение, как на рисунке выше, наблюдается на длинной истории — однако в пределах десятилетий может довольно сильно меняться:
Видно, что на протяжении 2000-2009 годов американские акции даже ушли в минус, в результате чего кривая получила движение вниз, а не вверх. Следовательно, корреляция ничего не говорит об абсолютной доходности — первая может мало меняться на протяжении 20 лет, однако результаты одинаковых портфелей на следующих друг за другом 10-летних промежутках разойдутся.
Так, в кризисные 70-е и растущие 80-е корреляция американских акций и 5-летних облигаций была в среднем одинакова (около 0.25), однако доходность портфеля 50 на 50 во втором случае была 15% годовых, а в первом лишь около 7%. Ниже отдельно показаны наилучшее и наихудшее американское десятилетие с 1950 года:
Как видим, отрицательная корреляция с 2000 года явилась причиной заметного выгиба кривой влево, в результате чего 5% доходности могли быть достигнуты с очень низким риском. Несомненно важным для инвестора является и корреляция других активов — в первую очередь американского и европейского рынков, стран Азии и пр. Детальный подход показывает разницу в их движениях — и следовательно, необходимость учитывать в своем портфеле рынки разных стран.
Источник