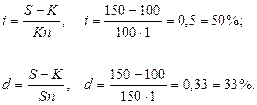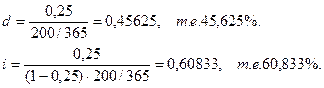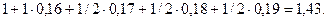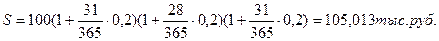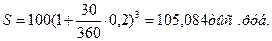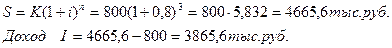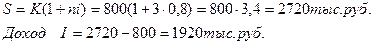Как определить доходность операции годовой сложной процентной ставкой

Формулы доходности финансовых операций

Если в формулах наращения по процентной и учетной ставке принять срок n = 1 году, то получим, что

.

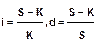
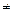
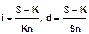
Если n1 году, .

Эти формулы принято называть формулами доходности или эффективности по простой ставке процентов и учетной ставке соответственно.

Предприятие получило кредит на 1 год в размере 100 млн. с условием возврата 150 млн.

Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок.

К = 100 млн., S = 150 млн., n = 1 год. I = ?, d = ?

Решение:

Дисконтная ставка всегда меньше процентной, ибо она учитывает время более жестко.

Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли (или процента) от суммы погасительного платежа. Таким образом, уровень процентной ставки задается в неявном виде. Выведем формулы, с помощью которых можно вычислить значения этих ставок.

Пусть S- размер погасительного платежа (сумма ссуды к концу срока),

d_n – доля этого платежа, определяющая величину дисконта за весь срок ссуды.

К = S(1 – d_n) – реально выдаваемая ссуда в момент заключения договора.

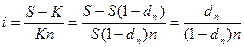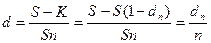Задача 7.

Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней.

Простые переменные ставки

В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.

Если i₁, i₂,… i_k – последовательные во времени простые ставки,

а n_1, n_2,… n_k – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:

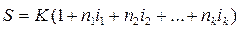Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.

Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года.

Множитель наращения =

Иначе, за 2,5 года начальный капитал увеличился в 1,43 раза.

Реинвестирование

В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!)

В этом случае наращенная сумма для всего срока составит:

(14) k – количество реинвестиций.

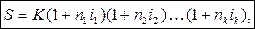
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:

, k – количество реинвестиций.

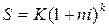
Задача 9.

Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам.

По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам.

По точным процентам:

(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!)

По банковским процентам при условии, что в каждом месяце по 30 дней:

Модуль 2. Сложные проценты

Наращение по сложным процентам

В среднесрочных и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты.

Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов.

Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид

(1) , где i — годовая (номинальная) процентная ставка, n — число лет начисления,

— множитель наращения по сложным процентам.

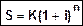
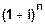
Задача 1.

Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

2. Простые проценты:

За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам.

Задача 2.

Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

Источник

Сложный процент. Формула сложного процента для вклада. Расчет сложных процентов

Сложным процентом принято называть эффект, когда проценты прибыли прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.
Формула сложного процента — это формула, по которой рассчитывается итоговая сумма с учётом капитализации (начислении процентов).

Простой расчет сложных процентов

Чтобы лучше усвоить расчет сложных процентов, давайте разберём пример.
Представим, что вы положили 10 000 руб в банк под 10 процентов годовых.
Через год на вашем банковском счету будет лежать сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль — 1000 рублей.
Вы решили оставить 11 000 руб на второй год в банке под те же 10 процентов.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.

Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.

Этот эффект и получил название сложный процент.

Когда вся прибыль прибавляется к основной сумме и в дальнейшем уже сама производит новую прибыль.

Формула сложного процента:

где
SUM — конечная сумма;
X — начальная сумма;
% — процентная ставка, процентов годовых /100;
n — количество периодов, лет (месяцев, кварталов).

Расчет сложных процентов: Пример 1.
Вы положили 50 000 руб в банк под 10% годовых на 5 лет. Какая сумма будет у вас через 5 лет? Рассчитаем по формуле сложного процента:

SUM = 50000 * (1 + 10/100) 5 = 80 525, 5 руб.

Сложный процент может использоваться, когда вы открываете срочный вклад в банке. По условиям банковского договора процент может начисляться например ежеквартально, либо ежемесячно.

Расчет сложных процентов: Пример 2.
Рассчитаем, какая будет конечная сумма, если вы положили 10 000 руб на 12 месяцев под 10% годовых с ежемесячным начислением процентов.

SUM = 10000 * (1+10/100/12) 12 = 11047,13 руб.

ПРИБЫЛЬ = 11047,13 — 10000 = 1047,13 руб

Доходность составила (в процентах годовых):

% = 1047,13 / 10000 = 10,47 %

То есть при ежемесячном начислении процентов доходность оказывается больше, чем при начислении процентов один раз за весь период.

Если вы не снимаете прибыль, тогда начинает работать сложный процент.

Формула сложного процента для банковских вкладов

На самом деле формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше. Процентная ставка для вклада (%) рассчитывается так:

% = p * d / y

где
p — процентная ставка (процентов годовых / 100) по вкладу,
например, если ставка 10,5%, то p = 10,5 / 100 = 0,105;
d — период (количество дней), по итогам которого происходит капитализация (начисляются проценты),
например, если капитализация ежемесячная, то d = 30 дней
если капитализация раз в 3 месяца, то d = 90 дней;
y — количество дней в календарном году (365 или 366).

То есть можно рассчитывать процентную ставку для различных периодов вклада.

Формула сложного процента для банковских вкладов выглядит так:

SUM = X * (1 + p*d/y) n

При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов. Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. Наглядно это можно увидеть на примере ниже.

Источник

Что такое годовая процентная доходность и как она рассчитывается?

Годовая процентная доходность – это годовой процент прибыли, полученной от инвестиций, который учитывает эффект сложных процентов.

Это полезный показатель, который нужно иметь под рукой, когда вы решаете, какой банк лучше всего и какой тип счета выбрать, чтобы максимизировать выплаты по процентам.

Если вы можете понять годовую процентную доходность, а также то, что отличает ее от простых процентов и как ее рассчитывать, это может помочь вам понять, как максимально использовать деньги, которые вы храните в банке.

Что такое годовая процентная доходность?

Годовая процентная доходность может быть определена как ставка, получаемая в результате заимствования или зарабатывания денег в течение года с учетом применения к депозитам или инвестиционным продуктам сложных процентов.

Как работает годовая процентная доходность

Если вы когда-либо регистрировали сберегательный счет, вы, вероятно, слышали или видели термин «годовая процентная доходность» или «APY».

Когда вы вносите средства на сберегательный счет, на денежный рынок или на депозитный сертификат (ДС), вы получаете проценты. APY точно сообщает вам, сколько процентов вы заработаете на счете в течение одного года, в зависимости от процентной ставки и частоты начисления сложных процентов, то есть процентов, которые вы зарабатываете на основную сумму (первоначальный депозит), плюс проценты с прибыли.

Почему годовая процентная доходность уникальна

По сравнению с простой процентной ставкой (без начисления сложных процентов) APY дает более точное представление о том, сколько вы будете зарабатывать на депозитном счете, поскольку учитывает начисление сложных процентов.

Начисление процентов происходит, когда вы получаете проценты как на деньги, которые вы инвестируете (или первоначальную основную сумму), так и на вашу прибыль (или прошлые накопленные проценты).

Пример единовременного годового платежа: Предположим, вы вносите 1000 долларов на сберегательный счет, на который выплачивается простая годовая процентная ставка 5%. Если ваш банк рассчитывает и выплачивает проценты только один раз в конце года, банк добавит 50 долларов на ваш счет. В конце года у вас будет 1050 долларов (при условии, что ваш банк выплачивает проценты только один раз в год).

Пример ежемесячного начисления сложных процентов: Теперь предположим, что банк ежемесячно рассчитывает и выплачивает проценты. Вы будете получать небольшие дополнения каждый месяц. В этом случае вы закончите год с 1051,16 доллара, что больше указанной процентной ставки в 5%.

Разница может показаться небольшой, но через много лет (или с более крупными депозитами) она может быть значительной. В таблице ниже обратите внимание на то, как прибыль немного увеличивается каждый месяц.

Период	Прибыль	Баланс
1	$ 4.17	$ 1004.17
2	$ 4.18	$ 1008.35
3	$ 4.20	$ 1012.55
4	$ 4.22	$ 1016.77
5	$ 4.24	$ 1021.01
6	$ 4.25	$ 1025.26
7	$ 4.27	$ 1029.53
8	$ 4.29	$ 1033.82
9	$ 4.31	$ 1038.13
10	$ 4.33	$ 1042.46
11	$ 4.34	$ 1046.80
12	$ 4.36	$ 1051.16

APR и APY

Годовая процентная ставка (APR) – это простая процентная ставка, которую банк взимает с вас в течение года по продуктам, включая ссуды и кредитные карты. Это похоже на годовой процентный доход, но без учета сложных процентов.

Ссуды по кредитной карте демонстрируют важность различения между годовой процентной ставкой и годовой процентной доходностью. Если у вас есть баланс, вы часто будете платить APY, превышающую указанную APR.

Это связано с тем, что эмитенты карт обычно добавляют процентные платежи к вашему балансу каждый месяц. В следующем месяце вы должны будете платить проценты сверх этих процентов. Это похоже на получение процентов сверх процентов, которые вы зарабатываете на сберегательном счете. Разница может быть незначительной, но разница есть. Чем больше ваш кредит и чем дольше вы должны, тем больше становится разница.

При ипотеке с фиксированной процентной ставкой годовая процентная ставка является более точной, потому что вы обычно не добавляете процентные платежи и не увеличиваете остаток по ссуде. Более того, годовая процентная ставка учитывает затраты на закрытие, которые увеличивают общую стоимость заимствования. Однако некоторые ссуды с фиксированной процентной ставкой действительно растут (если вы не оплачиваете процентные расходы по мере их начисления).

APY более точен, чем APR в некоторых ситуациях, потому что он говорит вам, сколько стоит ссуда как сложные процентные расходы. Но когда вы занимаете деньги, вы обычно видите только годовую процентную ставку. На самом деле вы можете платить APY, которая почти всегда выше для определенных типов ссуд.

Расчет APY с помощью электронной таблицы

Вы почти всегда будете видеть APY, указанную в банках, поэтому вам, как правило, не нужно делать какие-либо расчеты самостоятельно. Однако вы можете рассчитать APY самостоятельно, хотя это может быть непросто. Программное обеспечение для работы с электронными таблицами, такое как Microsoft Excel или Google Таблицы, может упростить задачу. Используйте электронную таблицу Google Таблицы для расчета APY или следуйте инструкциям ниже, чтобы создать свою собственную:

• Создайте новую таблицу.
• Введите процентную ставку (в десятичном формате) в ячейку A1.
• Введите частоту начисления сложных процентов в ячейку B1 (используйте «12» для помесячного или «1» для ежегодного).
• Вставьте следующую формулу в любую другую ячейку: =POWER((1+(A1/B1)),B1)-1

Например, если заявленная годовая ставка составляет 5%, введите «0,05» в ячейку A1. Затем для ежемесячного начисления сложных процентов введите «12» в ячейку B1.

Для ежедневного начисления сложных процентов вы можете использовать 365 или 360, в зависимости от вашего банка или кредитора.

В приведенном выше примере вы обнаружите, что APY составляет 5,116%. Другими словами, процентная ставка 5% с ежемесячным начислением сложных процентов приводит к годовому доходу в размере 5,116%. Попробуйте изменить частоту начисления сложных процентов, и вы увидите, как меняется APY. Например, вы можете показать ежеквартальное начисление сложных процентов (четыре раза в год) или один несчастный платеж в год, что даст 5% годовых.

Вычисление APY с помощью формулы

Если вы предпочитаете выполнять математические расчеты по старинке, вычислите APY вручную следующим образом:

APY = 100 [(1 + r/n)^n] – 1, где r – заявленная годовая процентная ставка в виде десятичного числа, а n – количество периодов начисления сложных процентов в год. (Карет («^») означает «возведены в степень.»)

Продолжая предыдущий пример, если вы получаете 51,16 доллара США процентов в течение года при балансе счета в 1000 долларов США, рассчитайте APY следующим образом:

• APY = 100 [(1 + .05/12)^12] – 1]
• APY = 5.116%

Финансовые эксперты могут признать это расчетом эффективной годовой ставки (EAR).

Вы также можете рассчитать годовую процентную доходность следующим образом:

APY = 100 [(1 + Процент/Основная сумма)^(365/Дни в срок) – 1], где проценты – это сумма полученных процентов, а основная сумма – это начальный депозит или остаток на счете.

Используя выплату процентов и остаток на счете из приведенного выше примера, рассчитайте APY следующим образом:

• APY = 100 [(1 + 51.16/1000)^(365/365) – 1]
• APY = 5.116%

Максимизация APY

Годовая процентная доходность увеличивается с более частыми периодами начисления сложных процентов. Если вы откладываете деньги на банковский счет, узнайте, как часто они накапливаются. Ежедневное или ежеквартальное начисление сложных процентов обычно лучше, чем годовое, но для уверенности проверьте APY для каждого счета.

Вы также можете увеличить APY самостоятельно, если посмотрите на все свои активы как на часть более широкой финансовой картины. Другими словами, не думайте об инвестиции в один депозитный сертификат (ДС) в отдельности от вашего текущего счета – все вложения должны работать вместе, помогая вам достичь ваших целей, и каждое из них должно располагаться соответствующим образом.

Чтобы максимизировать вашу личную годовую процентную доходность, убедитесь, что ваши деньги увеличиваются как можно чаще. Если два ДС дают одинаковую процентную ставку, выберите тот, который выплачивает проценты чаще (и, следовательно, имеет самую высокую процентную ставку). Вы можете автоматически реинвестировать свой процентный доход – чем чаще, тем лучше – и вы начнете получать больше процентов с этих процентных платежей.

Ключевые выводы

• Годовая процентная доходность – это годовой процент инвестиционной прибыли, который учитывает эффект сложных процентов.
• Это полезный показатель, который нужно иметь под рукой, особенно если вы можете отличить его от простых процентов и понять, как его рассчитать.
• Когда вы разберетесь с APY, вы сможете решить, как максимально использовать деньги, которые хранятся в банке.
• При расчете APY вручную используется следующая формула: APY = 100 [(1 + Процент/Основная сумма)^(365/Дни в срок) – 1]

Экономист, финансовый аналитик, трейдер, инвестор. Личные интересы – финансы, трейдинг, криптовалюты и инвестирование.

Источник