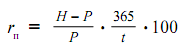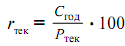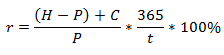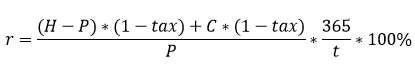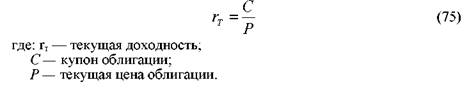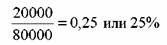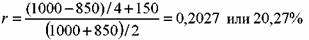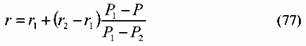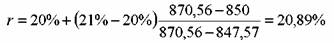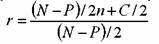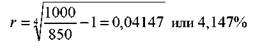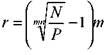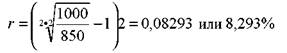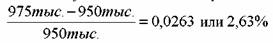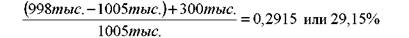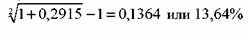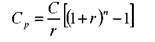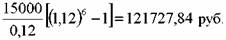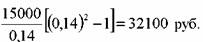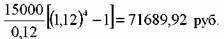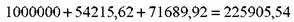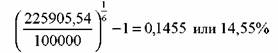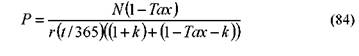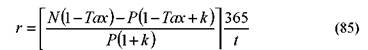Как определить доходность облигации за период владения

Как считать доходность облигаций

С помощью облигаций компании и государство берут деньги в долг. По облигациям регулярно выплачивают проценты — эти выплаты называют купонами. Затем тот, кто выпустил облигации, погашает их — выплачивает номинал владельцам ценных бумаг. Очень часто номинал одной облигации — 1000 Р .

Облигации похожи на вклад, но устроены сложнее. Доходность облигаций можно считать по-разному , а еще она зависит не только от купона, но и от цены. Можно сказать, что на бирже с помощью цены договариваются о доходности облигации: чем дешевле ее купите, тем больше на ней сможете заработать, и наоборот. Рассказываем, чем отличаются разные виды доходности облигаций и как их посчитать.

💸 Купонная доходность

Ставка купона показывает, какой процент от номинала облигации составляет сумма купонов за год. Это самый простой показатель, но, пожалуй, наименее полезный для выбора облигаций

Пример: по облигации «Лента БО-001 Р -04 » купоны выплачиваются каждые 182 дня в размере 31,41 Р , то есть около 63 Р за год. Номинал облигации — 1000 Р . Купонная доходность — 63 / 1000 = 6,3% годовых

📅 Текущая доходность

Цена облигации может отличаться от номинала, и это учтено в текущей доходности. Она считается так: размер купонов за год или ставку купона делят на нынешнюю цену облигации — в рублях или процентах от номинала

Пример: 7 сентября та же облигация «Ленты» стоила 101,2% номинала, или 1012 Р . Ставка купона — 6,3%, то есть в год платят 63 Р . Значит, текущая доходность такая: 63 / 1012 = 6,23% годовых. Она меньше купонной, потому что облигация торгуется дороже номинала

📈 Простая доходность к погашению

Показывает, сколько инвестор заработает, если купит облигацию по определенной цене с учетом накопленного купонного дохода и будет владеть ею до даты погашения. Полученные от облигаций деньги инвестор не вкладывает

Пример: 7 сентября эту облигацию можно было купить за 1012 Р + НКД 16,74 Р . Если владеть ею до погашения 31 мая 2023 года, можно получить 6 купонов по 31,41 Р , а в конце выплатят номинал — 1000 Р . Простая доходность к погашению — 5,69% годовых. Посчитать ее легко в специальных калькуляторах — о них чуть позже

📊 Эффективная доходность к погашению

Это как простая доходность к погашению, но с важным отличием. Считается, что все полученные купоны и амортизационные выплаты инвестор реинвестирует — вкладывает в ту же облигацию, причем под ту же доходность

Пример: все так же , но предполагаем, что на полученные купоны инвестор покупает дополнительные облигации. Эффективная доходность к погашению — 5,89% годовых. Она выше, чем простая к погашению, потому что помогает сложный процент

⏱ Доходность к оферте

У некоторых облигаций ставка купона известна только до даты оферты — это дата, когда можно попросить компанию досрочно погасить вашу облигацию. В таком случае простую и эффективную доходность считают не к дате погашения, а к дате ближайшей оферты

Пример: у облигации «АФК Система БО 001 Р -14 » погашение в июле 2030 года, но размер купонов известен только до оферты — она будет в апреле 2023. Из-за этого доходность к погашению нельзя посчитать, а доходность к оферте — можно

Источник

Доходность облигаций — расчет и формулы

Автор: Алексей Мартынов · Опубликовано 15.09.2014 · Обновлено 20.05.2017

Доходность облигаций рассчитывается на основе купонных платежей, цены погашения, сроков владения и цены облигации. Расчет доходности купонных и дисконтных облигаций различается.

Доходность дисконтных облигаций

Доход по дисконтной облигации инвестор получает за счет разницы между ценой покупки облигации и ценой погашения или продажи. Доходность дисконтных облигаций рассчитывается по формуле:

r — доходность облигации
H — цена погашения облигации или цена продажи
P — цена покупки облигации
t — количество дней владения облигацией
365 — число дней в году

Доходность выражается в процентах годовых.

Условный пример: номинал 1000 рублей, цена покупки 94% , время владения — год. r=(1000-940)/940 * 1* 100% = 6,38%

Доходность купонных облигаций

Доходность купонных облигаций бывает двух видов — текущая и доходность к погашению.

Текущая доходность облигации

Показывает отношение купонных выплат за год к текущей цене облигации.

С — сумма купонных выплат за год
Р — текущая цена облигации

Доходность облигации к погашению

Показывает, какую доходность получит инвестор, продержав облигацию до погашения. Ориентировочно доходность облигации рассчитывается по формуле

r — доходность облигации
H — цена погашения облигации, в случае продажи облигации до погашения H = цена продажи + полученный НКД.
P — цена покупки облигации + уплаченный НКД.
С — сумма купонных выплат за период владения облигацией
t — количество дней владения облигацией

Реальный пример: выпуск Банк ВТБ-21-боб

Статус: в обращении
Дата размещения:22.01.2013
Номинал 1000,
Текущая цена предложения 98,5%,
НКД — 9,82 рубля,
Ставка купона, годовых, 8,15%
Денежная величина купона 20,32 рублей
Текущий купон — 7 из 12, то есть еще осталось 6 купонов.
Дата погашения — 19.01.2016
Дней до погашения — 502

r=((1000-(985+9,82)) + 20,32*6)/(985+9,82)*(365/502)*100% = 9,28% — доходность облигации в процентах годовых. Выражение доходности в процентах годовых позволяет сравнить доходность облигаций с разным сроком владения.

Фактическая доходность рассчитывается так:

r=((1000-(985+9,82)) + 20,32*6)/(985+9,82)*100% = 12,77% — это фактическая доходность за все время владения до погашения (502 дня).

Учтите, что подоходный налог для физических лиц 13% и комиссии брокеру снижают доходность. C учетом налога формула будет такая:

где tax — текущая ставка налога на доходы физических лиц 0,13 (13%). Для ОФЗ, субфедеральных и муниципальных облигаций налог с купонного дохода не взимается.

Доходность облигаций

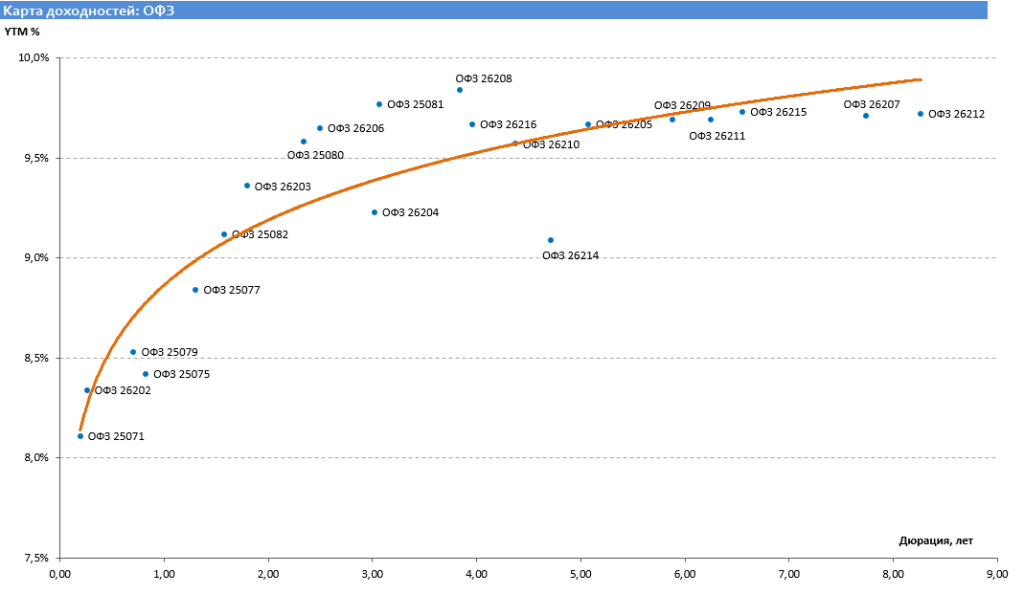
Доходность облигаций меняется со временем и зависит от процентных ставок в экономике, рыночной ситуации и эмитента. Самые низкодоходные облигации — государственные, самые доходные — корпоративные. Текущая доходность государственных облигаций федерального займа от 8 до 10% в зависимости от выпуска и дюрации. Доходность российских еврооблигаций, номинированных в иностранной валюте, от 1,5% до 6%.

Доходность облигаций федерального займа (сентябрь 2014)

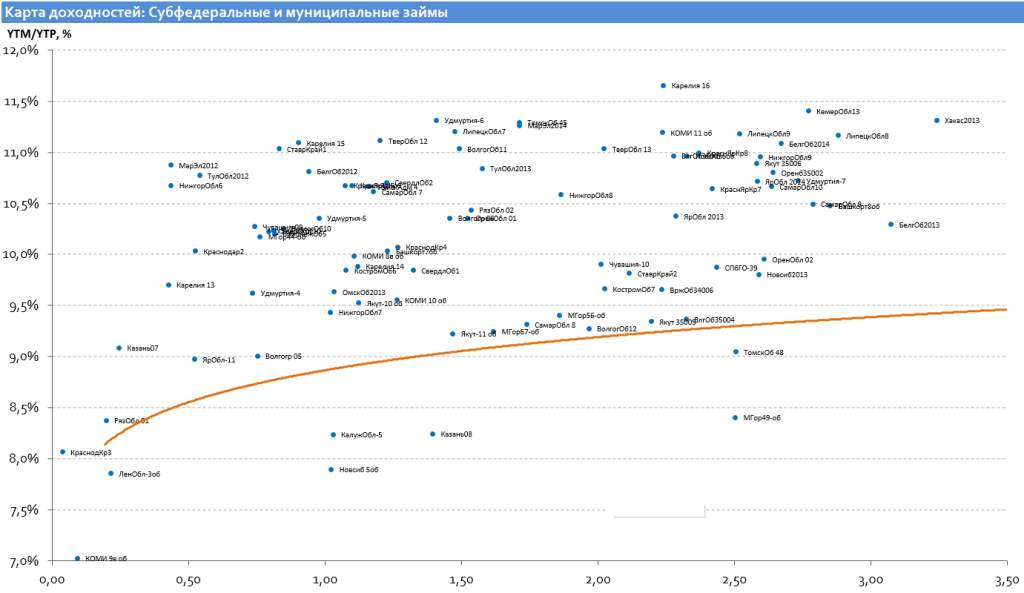
Доходность муниципальных облигаций чуть побольше.

Доходность муниципальных облигаций (сентябрь 2014)

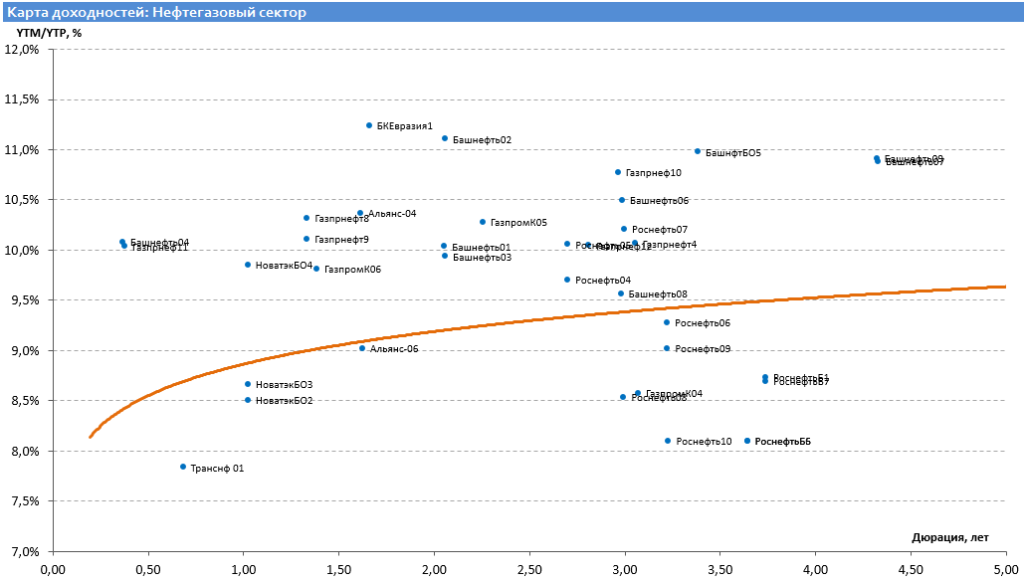
Доходность корпоративных облигаций колеблется в диапазоне от 7 до 15% в зависимости от сектора экономики и рейтинга надежности эмитента. Облигации отдельных эмитентов могут давать доходность больше 15%. Корпоративные еврооблигации, номинированные в долларах, дают доходность от 3 до 10%.

Доходность корпоративных облигаций, нефтегазовый сектор (сентябрь 2014)

Еще раз повторюсь, что это текущие ставки доходности, в текущих рыночных условиях и экономических реалиях, приведены исключительно в качестве примера, и через год они могут быть совсем другие.

Источник

Материалы

Определение доходности облигаций

• » onclick=»window.open(this.href,’win2′,’status=no,toolbar=no,scrollbars=yes,titlebar=no,menubar=no,resizable=yes,width=640,height=480,directories=no,location=no’); return false;» rel=»nofollow»> Печать
• E-mail

Подробности Подробности Категория: Оценка ценных бумаг — статьи Опубликовано: 26.11.2013 17:59 Автор: Administrator Просмотров: 11890

Определение доходности облигаций

Определение доходности купонной облигации

Текущая доходность

Текущая доходность определяется по формуле:

С = 20000 руб., Р = 80000 руб. Определить текущую доходность облигации. Она равна:

представляет собой как бы фотографию доходности облигации на данный момент времени. В знаменателе формулы (75) стоит текущая цена облигации. В следующий момент она может измениться, тогда изменится и значение текущей доходности.

Показателем текущей доходности удобно пользоваться, когда до погашения облигации остается немного времени, так как в этом случае ее цена вряд ли будет испытывать существенные колебания.

Доходность до погашения.

Более объективным показателем доходности является доходность до погашения, так как при ее определении учитывается не только купон и цена бумаги, но и период времени, который остается до погашения, а также скидка или премия относительно номинала. Доходность облигации можно вычислить из формулы (63). Поскольку она содержит степени, то сразу определить доходность можно только с помощью специальной компьютерной программы. Можно воспользоваться также методом подстановки. Он состоит в том, что в формулу (63) последовательно подставляют различные значения доходности до погашения и определяют соответствующие им цены. Операцию повторяют до тех пор, пока значение рассчитанной цены не совпадет с заданной ценой. При совпадении цен мы получим искомую величину доходности до погашения. Поскольку цена и доходность облигации связаны обратной зависимостью, то в ходе подстановки, получив цену, которая выше данной, необходимо увеличить следующую цифру доходности, подставляемую в формулу. Если рассчитанная цена оказалась ниже заданной, необходимо уменьшить значение доходности.

где: r — доходность до погашения; N — номинал облигации; Р — цена облигации; п — число лет до погашения; С — купон.

N =1000 руб., Р = 850 руб., n = 4 года, купон равен 15%. Определить доходность до погашения облигации. Она равна:

формулы (76) тем больше, чем больше цена облигации отличается от номинала и чем больше лет остается до погашения облигации. Если бумага продается со скидкой, то формула (76) дает заниженное значение доходности облигации, если с премией, то завышенное.

После того как инвестор определил значение доходности облигации с помощью формулы (76), он может воспользоваться формулой (77) для вычисления точной цифры доходности:

по формуле (77) сводится к следующему. Вкладчик выбирает значение г1 которое ниже полученного значения ориентировочной доходности, и рассчитывает для него соответствующую цену облигации Pi, воспользовавшись формулой (63). Далее берет значение r2 которое выше значения ориентировочной доходности, и рассчитывает для него цену Р2. Полученные значения подставляются в формулу (77).

Определить точную величину доходности облигации из приведенной выше задачи.

Мы рассчитали, что ориентировочная доходность облигации равна 20, 27%. Поэтому возьмем r1, = 20% и r2 = 21%. Тогда P1 = 870, 56 руб. и Р2 = 847, 57 руб.

Таким образом, купив облигацию за 850 руб., инвестор обеспечит себе доходность до погашения равную 20, 89%.

Сделаем еще одно замечание. В формуле (76) купон выплачивался один раз в год. Соответственно в ответах получалось значение r равное простому проценту в расчете на год. Если по облигации купон выплачивается т раз в год, то можно пользоваться указанной формулой без всяких корректировок, т. е. не умножать количество лет на т и не делить купон на т. В этом случае мы также получим доходность бумаги как простой процент в расчете на год. В то же время, можно определить значение доходности, сделав указанную корректировку. Например, для облигации, по которой купон выплачивается два раза в год, формула ориентировочной доходности примет следующий вид:

является доходностью за полгода. Чтобы получить доходность за год, необходимо полученное значение умножить на 2.

5. 1. 2. 2. Определение доходности бескупонной облигации

вытекает из формулы (71).

N = 1000 руб., Р = 850 руб., п = 4 года. Определить доходность облигации. Она равна:

часть купонных облигаций имеет купоны, которые выплачиваются т раз в год, то формулу (78) необходимо скорректировать на величину m, т. е.:

N = 1000 руб., Р = 850 руб, n = 2 года, т = 2. Определить доходность облигации. Она равна:

5. 2. 1. 3. Определение доходности ГКО

Доходность ГКО определяется из формулы (74), а именно:

где: N— номинал ГКО; Р—цена ГКО; t — число дней с момента покупки облигации до дня погашения.

5. 1. 2. 4. Определение доходности ОФЗ-ПК и ОГСЗ

По ОФЗ-ПК и ОГСЗ выплачиваются плавающие купоны. Поэтому доходность до погашения данных облигаций можно определить только ориентировочно на основе оценки будущей конъюнктуры рынка.

В то же время ЦБ РФ дал следующую формулу для расчета доходности данных облигаций.

;

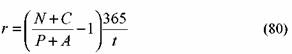
С— купон за текущий период;

Р — чистая цена облигации;

А — накопленный с начала купонного периода доход по купону;

t — количество дней до окончания текущего купонного периода.

Величина текущего купонного платежа С рассчитывается по формуле:

Т— количество дней в текущем купонном периоде.

.

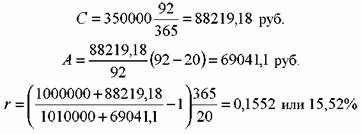
Определить доходность облигации.

5. 1. 2. 5. Доходность за период

До настоящего момента мы рассматривали главным образом доходность, которую инвестор может получить, если продержит облигацию до погашения. На практике вкладчика интересует также вопрос о доходности, которую он себе обеспечил, если продал облигацию раньше срока погашения. Другими словами, необходимо уметь рассчитать доходность за период. Доходность за период определяется как отношение дохода, полученного по облигации за этот период, к уплаченной за нее цене.

Вкладчик купил ГКО за 950 тыс. руб. и продал через 20 дней за 975 тыс. руб. В данном случае доходность за период составила:

в 2, 63% инвестор получил за 20 дней. Обычно величину доходности пересчитывают в расчете на год, чтобы ее можно было сравнить с другими инвестициями. Как известно из главы 3, возможно пересчитать данную доходность в расчете на год на основе простого или сложного процента. В случае простого процента она составила:

365 2,63% =48,00% 20 В случае сложного процента она равна:

(1+ 0,0263)365/ 20 -1= 0,6060 или 60,60%

Инвестор купил облигацию по цене 1005 тыс. руб. и продал ее через два года за 998 тыс. руб. За двухлетний период он получил купонные платежи в сумме 300 тыс. руб.

Доходность за период составила:

Данная доходность получена в расчете на двухлетний период.

5. 1. 3. Реализованный процент

5. 1. 3. 1. Определение доходов, которые инвестор получит по облигации

суммы погашения при выкупе облигации или суммы от ее

где: С_р — сумма купонных платежей и процентов от реинвестирования купонов;

С — купон облигации;

п — число периодов, за которые выплачиваются купоны;

r — процент, под который вкладчик планирует реинвестировать купонные платежи.

Инвестор приобретает облигацию по номиналу, номинал равен 100 тыс. руб., купон — 15%, выплачивается один раз в год. До погашения остается 6 лет. Инвестор полагает, что за этот период он сможет реинвестировать купоны под 12% годовых. Определить общую сумму средств, которые вкладчик получит по данной бумаге, если продержит ее до момента погашения.

Через шесть лет инвестору выплатят номинал облигации. Сумма купонных платежей и процентов от их реинвестирования составит:

сумма средств, которые получит инвестор за шесть лет, равна 221727, 84 руб.

За оставшиеся четыре года полученная сумма, поскольку она инвестирована под 14%, возрастет до:

последних лет составит:

Если вкладчик планирует в будущем продать облигацию, то ему необходимо оценить ее стоимость к этому моменту времени и прибавить к сумме купонов и процентов от их реинвестирования.

Определение реализованного процента

Реализованный процент — это процент, позволяющий приравнять сумму всех будущих поступлений, которые инвестор планирует получить по облигации, к ее сегодняшней цене. Он определяется по формуле:

S — цена покупки облигации. Для последнего примера реализованный процент равен:

процент позволяет принимать решения, исходя из ожиданий развития конъюнктуры рынка.

Определение цены и доходности облигации с учетом налоговых и комиссионных платежей

До настоящего момента мы определяли значения цены и доходности облигаций, не учитывая тот факт, что по ним могут взиматься налоги и выплачиваться комиссионные вознаграждения брокерским компаниям.

Данные поправки легко сделать, скорректировав соответствующим образом формулы определения цены и доходности, рассмотренные выше. Корректировка формул заключается в том, что получаемую прибыль уменьшают на величину взимаемых налогов и на размер уплаченных комиссионных. В качестве затрат учитывается не только цена, по которой покупается бумага, но и комиссионные брокерской фирмы. Приведем пример такой корректировки для ГКО. Так формулы (74) и (79) соответственно примут вид:

где: T_ax — ставка налога на ГКО (ставка налога подставляется в формулу в десятичном значении, например, налог 15% следует учесть в формуле как 0, 15);

k — комиссионные платежи как процент от суммы сделки (учитывается в формуле в десятичных значениях).

Источник