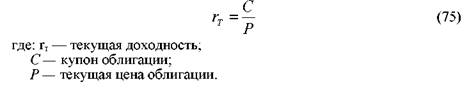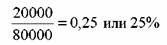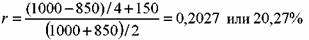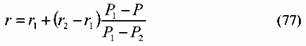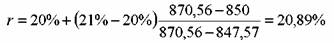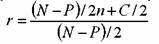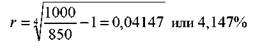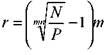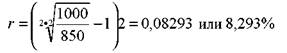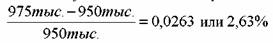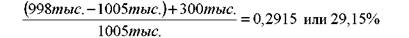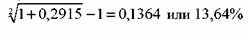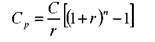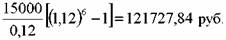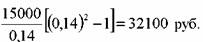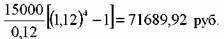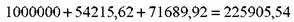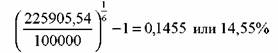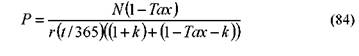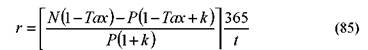Определение доходности инвестиций в ГКО и МКО
ГКО (МКО) являются краткосрочными бескупонными государственными (муниципальными) облигациями. Схема расчета публикуемых доходностей к погашению одинакова.
Численный пример. Цена на торгах СПб валютной биржи 11.04.97 г. по выпуску МКО SV34010GSPMO составляла 70,80 (в % к номиналу), на дату погашения 22.04.98 г. инвестор получит 100% номинала («Финансовые известия». 1997. N 277).
Доходность инвестиций за весь период до погашения составляет (в процентах):
Номинальная доходность к погашению (YTM) равна:
При вычислении эффективной доходности используется приведение по схеме сложных процентов. Искомая величина находится из условия:
r = (1,412 — 1) x 100 = 39,8%.
Определение доходности инвестиций в ОФЗ и ОГСЗ
Облигации федерального займа (ОФЗ) дают как дисконтный, так и купонный доход, выплачиваемый ежеквартально или раз в полгода, при этом ставка купона переменна и объявляется только на ближайший купонный период.
Аналогичная ситуация характерна и для облигаций государственного сберегательного займа (ОГСЗ).
Официально принятая схема исчисления доходности к погашению (YTM) исходит только из этой известной купонной выплаты.
Численный пример. Цена закрытия на биржевых торгах 01.04.97 г. по выпуску 24010 с датой погашения 17.06.98 г. и датой ближайшей купонной выплаты 11.06.97 г. составляла 97,74% к номиналу. Объявленный купонный
процент равен 37,68% годовых, т.е. выплата будет равна ─── x 37,68% =
18,79%, поскольку купонный период по этому выпуску равна 182 дням. Однако
при покупке придется доплатить накопленный купонный доход. Так как до
ближайшей купонной выплаты остается 71 день, величина этого дохода равна
YTM рассчитывается следующим образом:
365 100 + 18,79 — 97,74 — 11,46
т.е. исходя из того, что через 71 день, оставшийся до купонной выплаты, можно продать облигацию по номиналу.
Необходимо учесть, что полученное YTM не пригодно при сравнении доходности ОФЗ с другими государственными бумагами, даже имеющими аналогичные даты погашения.
Сравним, например, ГКО выпуск 22077 со сроком до погашения 288 дней, продаваемый 01.04.97 г. по цене 77,64% номинала, и ОФЗ выпуск 24006 со сроком до погашения 309 дней.
Купонный период равен 91 дню, до ближайшего купонного платежа с номинальным годовым процентом 29,28% в данный день остается 36 дней, после чего будут еще 3 купонных платежа с заранее не известной ставкой.
Облигации ОФЗ продаются по цене 98,65 с добавлением накопленного купонного дохода:
Номинальная доходность к погашению (YTM) ГКО равна:
Эффективная доходность ГКО составляет:
r = [(1 + ─────) — 1] x 100 = 37,8%.
Эту величину можно принять в качестве ставки приведения для оценки инвестиций в ОФЗ. В предположении неизменности купонной ставки получим:
127/365 218/365 309/365
(1 + r/100) (1 + r/100) (1 + r/100)
Таким образом, даже если ставка останется прежней, вложения в ОФЗ менее эффективны, чем в ГКО, хотя публикуемая YTM для ОФЗ выше и составляет
365 100 + 29,28 x (91/365)
Необходимость сравнения с учетом динамики купонных ставок особенно ясна при решении вопроса о выборе предпочтительного выпуска ОФЗ или серии ОГСЗ из числа присутствующих на рынке и имеющих существенно различные сроки до погашения. Однако при этом важно учесть и динамику ставок приведения, поскольку эффективность альтернативных инвестиций (например, в ГКО) также падает, что может частично компенсировать падение купонных ставок.

Приведем численный пример такого сравнения эффективности вложений в различные серии ОГСЗ. Расчеты были проведены по данным, располагаемым на 26.11.96 г.
При этом предполагалось, что как купонные платежи, так и ставки приведения будут падать экспоненциально с одним и тем же темпом а:
P = (P — P ) x a + P , r = (r — r ) x a + r ,
t 0 беск. беск. t 0 беск. беск.
где P — текущий (на день расчета) известный уровень ближайшего
0 купонного платежа (в %),
r — текущая ставка приведения,
r = P — прогнозируемый уровень ставок в достаточно далеком
беск. беск. будущем (более двух лет).
Согласно прогнозам, было принято: a = 0,87, r_беск. = 10%, причем за единицу времени был принят квартал (91 день).
Рекомендуется выбрать выпуск ОГСЗ, для которого NPV окажется наибольшим.
Расчет NPV производится по формуле с переменной ставкой приведения:
(1 + r ) 1 + r (1 + r )(1 + r )
— P — цена на дату расчета (включающая накопленный купонный доход);
— P P — купонные платежи;
— r r — процентные ставки за квартал (годовые, деленные на
1, . 4 4), известные или прогнозируемые на моменты выплат
соответствующих купонных платежей;
— t = n/91, где n — число дней до ближайшего платежа.
Все платежи, произведенные ранее (до даты расчета), не учитываются.
Результаты расчетов сведены в табл.П4.4.
Таблица П4.4
│Серия ОГСЗ │ IV │ V │ VI │ VII │ VIII │ IX │
│Даты │28.09.96 г.│10.01.97 г.│17.01.97 г.│22.02.97 г.│11.12.96 г.│02.01.97 г.│
│выплат │28.02.97 г.│10.04.97 г.│17.04.97 г.│22.05.97 г.│11.03.97 г.│02.04.97 г.│
│Купонные │ 58,48* │ 55,02* │ 48,54* │ 48,23 │ 60,00* │ 60,08 │
│выплаты │ 41,92 │ 39,65 │ 35,38 │ 35,13 │ 42,93 │ 42,98 │
│(% годовых) │ │ │ │ │ 31,68 │ 31,72 │
│26.09.96 (%)│ 117,20 │ 112,00 │ 110,00 │ 121,90 │ 116,10 │ 114,30 │
│NPV │ -4,95 │ -0,24 │ -0,63 │ -2,45 │ 1,70 │ 4,45 │
Выплаты, отмеченные*, были известны, остальные прогнозировались. Исходная (текущая) ставка приведения r_o принималась равной 32,4%.
Вывод, вытекающий из расчета, ясен:
следует инвестировать в самую «дальнюю» серию XI. Вместе с тем если ориентироваться на YTM, рассчитанную по официальной методике с учетом только ближайшего купонного платежа, то преимущество получит V и VI серии, и это преимущество иллюзорно.
Оценка доходности инвестиций в акции
Для инвестора важно знать, насколько эффективными окажутся вложения капитала в покупку акций. Однако эта эффективность не может быть рассчитана точно, поскольку она зависит от неизвестного курса продажи акций в будущем и заранее неизвестных дивидендных выплат.
Некоторую ориентацию дают сведения об эффективности вложений в прошлом.
Пусть инвестор принимает решение 25.04.97 г., зная средние цены сделок в Российской торговой системе (РТС) на эту дату, например:
акции РАО ЕЭС — 0,213 долл.;
акции «Мосэнерго» — 1,24 долл.
Эти цены можно сравнить с теми, которые были в прошлом, например 1,5 года назад, 15.10.95 г.:
акции РАО ЕЭС — 0,0264 долл.;
акции «Мосэнерго» — 0,31 долл.
Это позволяет рассчитать доходность операции «купил 25.10.95 г. — продал 25.04.97 г.». Без учета дивидендных выплат они равны соответственно:
0,213 — 0,0264 1,24 — 0,31
Приведем эти доходности к стандартному годовому периоду:
r = [(1 + 7,068) — 1] x 100 = 302%;
r = [(1 + 3,00) — 1] x 100 = 152%.
В условиях нестабильного рынка нельзя ожидать на будущий год, т.е. при покупке акций 25.04.97 г. и продаже 25.04.98 г., получить ту же доходность. Однако полезно сравнить полученные величины с безрисковой доходностью инвестиций в ГКО за тот же период, равной 160% годовых, и убедиться, что инвестиции в акции РАО ЕЭС давали почти вдвое больше и это оправдывает риск, связанный с нестабильностью цен.
Однако оценивать эффективность по изменению курсовой стоимости между произвольно взятыми датами опасно. Действительно, если в день покупки цена случайно была резко ниже средней, а в день продажи — резко выше, то доходность увеличится, однако этот одиночный факт малополезен для прогноза эффективности в будущем.
Другой, более надежный вариант оценки по «предыстории» ориентируется на данные по эффективностям краткосрочных операций типа «купил — продал через две недели». Располагая данными о торгах в прошлом, можно убедиться, что эффективности таких операций сильно менялась, была нестабильной. Однако можно рассчитать ее среднюю величину*(10). Для тех же акций получим:
r(14) = 10,3%; r(14) = 13,1%,
или, пересчитывая средние двухнедельные в годовые,
r = 11,8 = 1180%; r = 23,5 = 2350%.
Эти величины показывают, что эффективность краткосрочных, спекулятивных операций может быть много выше эффективности консервативных инвестиций на длительный период, Однако надо понимать их условность. В частности, здесь не учитываются операционные затраты (комиссионные и т.п.).
Главное же, что такие операции более рискованны: в действительности эффективность каждой из них сильно отличается от средней.
Можно рассчитать стандартные (среднеквадратичные) отклонения от средней эффективности. Для данных акций они равны:
сигма = 15,3%, сигма = 23,7%,
т.е. случайные отклонения больше средних значений (данные по 2-нeдeльным операциям).
Более полная картина оценки эффективности инвестиций в рисковые ценные бумаги может быть дана только при анализе портфельных инвестиций (см. ниже).
Источник
Материалы
Определение доходности облигаций
- » onclick=»window.open(this.href,’win2′,’status=no,toolbar=no,scrollbars=yes,titlebar=no,menubar=no,resizable=yes,width=640,height=480,directories=no,location=no’); return false;» rel=»nofollow»> Печать
Подробности Подробности Категория: Оценка ценных бумаг — статьи Опубликовано: 26.11.2013 17:59 Автор: Administrator Просмотров: 11889
Определение доходности облигаций
Определение доходности купонной облигации
Текущая доходность
Текущая доходность определяется по формуле:
С = 20000 руб., Р = 80000 руб. Определить текущую доходность облигации. Она равна:
представляет собой как бы фотографию доходности облигации на данный момент времени. В знаменателе формулы (75) стоит текущая цена облигации. В следующий момент она может измениться, тогда изменится и значение текущей доходности.
Показателем текущей доходности удобно пользоваться, когда до погашения облигации остается немного времени, так как в этом случае ее цена вряд ли будет испытывать существенные колебания.
Доходность до погашения.
Более объективным показателем доходности является доходность до погашения, так как при ее определении учитывается не только купон и цена бумаги, но и период времени, который остается до погашения, а также скидка или премия относительно номинала. Доходность облигации можно вычислить из формулы (63). Поскольку она содержит степени, то сразу определить доходность можно только с помощью специальной компьютерной программы. Можно воспользоваться также методом подстановки. Он состоит в том, что в формулу (63) последовательно подставляют различные значения доходности до погашения и определяют соответствующие им цены. Операцию повторяют до тех пор, пока значение рассчитанной цены не совпадет с заданной ценой. При совпадении цен мы получим искомую величину доходности до погашения. Поскольку цена и доходность облигации связаны обратной зависимостью, то в ходе подстановки, получив цену, которая выше данной, необходимо увеличить следующую цифру доходности, подставляемую в формулу. Если рассчитанная цена оказалась ниже заданной, необходимо уменьшить значение доходности.
где: r — доходность до погашения; N — номинал облигации; Р — цена облигации; п — число лет до погашения; С — купон.
N =1000 руб., Р = 850 руб., n = 4 года, купон равен 15%. Определить доходность до погашения облигации. Она равна:
формулы (76) тем больше, чем больше цена облигации отличается от номинала и чем больше лет остается до погашения облигации. Если бумага продается со скидкой, то формула (76) дает заниженное значение доходности облигации, если с премией, то завышенное.
После того как инвестор определил значение доходности облигации с помощью формулы (76), он может воспользоваться формулой (77) для вычисления точной цифры доходности:
по формуле (77) сводится к следующему. Вкладчик выбирает значение г1 которое ниже полученного значения ориентировочной доходности, и рассчитывает для него соответствующую цену облигации Pi, воспользовавшись формулой (63). Далее берет значение r2 которое выше значения ориентировочной доходности, и рассчитывает для него цену Р2. Полученные значения подставляются в формулу (77).
Определить точную величину доходности облигации из приведенной выше задачи.
Мы рассчитали, что ориентировочная доходность облигации равна 20, 27%. Поэтому возьмем r1, = 20% и r2 = 21%. Тогда P1 = 870, 56 руб. и Р2 = 847, 57 руб.
Таким образом, купив облигацию за 850 руб., инвестор обеспечит себе доходность до погашения равную 20, 89%.
Сделаем еще одно замечание. В формуле (76) купон выплачивался один раз в год. Соответственно в ответах получалось значение r равное простому проценту в расчете на год. Если по облигации купон выплачивается т раз в год, то можно пользоваться указанной формулой без всяких корректировок, т. е. не умножать количество лет на т и не делить купон на т. В этом случае мы также получим доходность бумаги как простой процент в расчете на год. В то же время, можно определить значение доходности, сделав указанную корректировку. Например, для облигации, по которой купон выплачивается два раза в год, формула ориентировочной доходности примет следующий вид:
является доходностью за полгода. Чтобы получить доходность за год, необходимо полученное значение умножить на 2.
5. 1. 2. 2. Определение доходности бескупонной облигации
вытекает из формулы (71).
N = 1000 руб., Р = 850 руб., п = 4 года. Определить доходность облигации. Она равна:
часть купонных облигаций имеет купоны, которые выплачиваются т раз в год, то формулу (78) необходимо скорректировать на величину m, т. е.:
N = 1000 руб., Р = 850 руб, n = 2 года, т = 2. Определить доходность облигации. Она равна:
5. 2. 1. 3. Определение доходности ГКО
Доходность ГКО определяется из формулы (74), а именно:
где: N— номинал ГКО; Р—цена ГКО; t — число дней с момента покупки облигации до дня погашения.
5. 1. 2. 4. Определение доходности ОФЗ-ПК и ОГСЗ
По ОФЗ-ПК и ОГСЗ выплачиваются плавающие купоны. Поэтому доходность до погашения данных облигаций можно определить только ориентировочно на основе оценки будущей конъюнктуры рынка.
В то же время ЦБ РФ дал следующую формулу для расчета доходности данных облигаций.
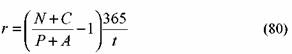
С— купон за текущий период;
Р — чистая цена облигации;
А — накопленный с начала купонного периода доход по купону;
t — количество дней до окончания текущего купонного периода.
Величина текущего купонного платежа С рассчитывается по формуле:
Т— количество дней в текущем купонном периоде.
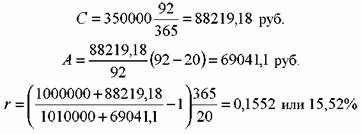
Определить доходность облигации.
5. 1. 2. 5. Доходность за период
До настоящего момента мы рассматривали главным образом доходность, которую инвестор может получить, если продержит облигацию до погашения. На практике вкладчика интересует также вопрос о доходности, которую он себе обеспечил, если продал облигацию раньше срока погашения. Другими словами, необходимо уметь рассчитать доходность за период. Доходность за период определяется как отношение дохода, полученного по облигации за этот период, к уплаченной за нее цене.
Вкладчик купил ГКО за 950 тыс. руб. и продал через 20 дней за 975 тыс. руб. В данном случае доходность за период составила:
в 2, 63% инвестор получил за 20 дней. Обычно величину доходности пересчитывают в расчете на год, чтобы ее можно было сравнить с другими инвестициями. Как известно из главы 3, возможно пересчитать данную доходность в расчете на год на основе простого или сложного процента. В случае простого процента она составила:
365 2,63% =48,00% 20 В случае сложного процента она равна:
(1+ 0,0263)365/ 20 -1= 0,6060 или 60,60%
Инвестор купил облигацию по цене 1005 тыс. руб. и продал ее через два года за 998 тыс. руб. За двухлетний период он получил купонные платежи в сумме 300 тыс. руб.
Доходность за период составила:
Данная доходность получена в расчете на двухлетний период.
5. 1. 3. Реализованный процент
5. 1. 3. 1. Определение доходов, которые инвестор получит по облигации
суммы погашения при выкупе облигации или суммы от ее
где: Ср — сумма купонных платежей и процентов от реинвестирования купонов;
С — купон облигации;
п — число периодов, за которые выплачиваются купоны;
r — процент, под который вкладчик планирует реинвестировать купонные платежи.
Инвестор приобретает облигацию по номиналу, номинал равен 100 тыс. руб., купон — 15%, выплачивается один раз в год. До погашения остается 6 лет. Инвестор полагает, что за этот период он сможет реинвестировать купоны под 12% годовых. Определить общую сумму средств, которые вкладчик получит по данной бумаге, если продержит ее до момента погашения.
Через шесть лет инвестору выплатят номинал облигации. Сумма купонных платежей и процентов от их реинвестирования составит:
сумма средств, которые получит инвестор за шесть лет, равна 221727, 84 руб.
За оставшиеся четыре года полученная сумма, поскольку она инвестирована под 14%, возрастет до:
последних лет составит:
Если вкладчик планирует в будущем продать облигацию, то ему необходимо оценить ее стоимость к этому моменту времени и прибавить к сумме купонов и процентов от их реинвестирования.
Определение реализованного процента
Реализованный процент — это процент, позволяющий приравнять сумму всех будущих поступлений, которые инвестор планирует получить по облигации, к ее сегодняшней цене. Он определяется по формуле:
S — цена покупки облигации. Для последнего примера реализованный процент равен:
процент позволяет принимать решения, исходя из ожиданий развития конъюнктуры рынка.
Определение цены и доходности облигации с учетом налоговых и комиссионных платежей
До настоящего момента мы определяли значения цены и доходности облигаций, не учитывая тот факт, что по ним могут взиматься налоги и выплачиваться комиссионные вознаграждения брокерским компаниям.
Данные поправки легко сделать, скорректировав соответствующим образом формулы определения цены и доходности, рассмотренные выше. Корректировка формул заключается в том, что получаемую прибыль уменьшают на величину взимаемых налогов и на размер уплаченных комиссионных. В качестве затрат учитывается не только цена, по которой покупается бумага, но и комиссионные брокерской фирмы. Приведем пример такой корректировки для ГКО. Так формулы (74) и (79) соответственно примут вид:
где: Tax — ставка налога на ГКО (ставка налога подставляется в формулу в десятичном значении, например, налог 15% следует учесть в формуле как 0, 15);
k — комиссионные платежи как процент от суммы сделки (учитывается в формуле в десятичных значениях).
Источник