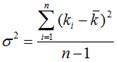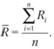Как определить дисперсию доходности
2 Дисперсия и стандартное отклонение.
Дисперсия — это мера разброса возможных исходов относительно ожидаемого значения. Следовательно, чем выше дисперсия, тем больше разброс, а значит и риск. Формула для расчета дисперсии следующая:

где ri — доходность актива;
r сред — ожидаемая (средняя) доходность актива;
n — число наблюдений.
Показатель дисперсии измеряют в процентах в квадрате и так как такая интерпретация очень непривычна и тяжела, в качестве другого показателя отклонения значений доходности от ожидаемого значения используется «среднее квадратическое отклонение» (стандартное отклонение), которое является квадратным корнем из дисперсии.

Приведем пример расчета дисперсии и стандартного отклонения при помощи Excel на основе имеющихся данных РАО ЕЭС, Лукойла и Ростелекома, пользуясь встроенными функциями ДИСП и СТАНДОТКЛОН.
Рисунок 2.16 – Вид с формулами
В результате получим:
Рисунок 2.17 – Дисперсии и стандартные отклонения
Итак, можно смело констатировать, что наиболее рискованной бумагой является Ростелеком. Ожидаемая ежемесячная доходность -1.08% при риске 9.44%.а наименее рискованной бумагой является Лукойл. Необходимо отметить, что не всегда актив, имеющий наибольшее стандартного отклонение является самым рискованным. Поэтому, прежде чем использовать стандартное отклонение в качестве меры относительного риска нужно рассчитать риск, приходящийся на единицу доходности при помощи коэффициента вариации. Этот показатель рассмотрен не будет, т.к. применительно к портфельной теории он не обязателен.
Зная ожидаемые доходности и показатели риска (стандартное отклонение), необходимо произвести еще ряд расчетов по определению коэффициентов ковариации и корреляция. После расчета данных коэффициентов станет возможным формирование портфелей, соответствующих нашим требованиям по риску и доходности.
Источник
Дисперсия как мера финансового инвестиционного риска. Оценка дисперсии и среднеквадратического отклонения доходности ценных бумаг.
В статистике дисперсия или вариация является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.
Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:
где ki – доходность ценной бумаги или актива при i-ом варианте исхода событий;

pi – вероятность i-го варианта исхода событий.
В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:
где ki – i-ое значение доходности ценной бумаги;

n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:
Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.
Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.
Под риском можно понимать вероятность возникновения каких-либо отклонений от ожидаемого события. Основополагающими мерами риска финансового актива являются такие показатели, как стандартное отклонение (σ) и дисперсия (D = σ2) сто доходности. В качестве синонима понятия «стандартное отклонение» используют также термин «волатильность». Стандартное отклонение и дисперсия доходности актива отражают степень возможного разброса его фактической доходности вокруг его средней (наиболее вероятной) доходности. Данные меры риска можно определить на основе прошлых данных статистики доходности актива.
Доходность актива на рассматриваемом интервале определяется следующим образом:
где St-1 – стоимость актива в начале интервала наблюдения; St – стоимость актива в конце интервала наблюдения.
Пусть имеются значения доходности акции за п равных интервалов наблюдения. За первый интервал она составила величину R1, за второй – R2 и т.д., за п-й интервал – Rn
Средняя доходность актива за наблюдаемый период (R) рассчитывается по формуле
Дисперсия доходности актива определяется как мера разброса наблюдаемой доходности (в процентах) от ее математического ожидания (средней величины). Формула генеральной дисперсии имеет вид
В случае если количество наблюдений незначительно (меньше 30), то для получения несмещенной оценки рекомендуется использовать так называемую исправленную дисперсию:
Показателем, характеризующим относительный уровень риска финансового актива, является стандартное отклонение его доходности от ожидаемой (средней за период):
При этом оценка допустимого уровня стандартного отклонения является субъективной и характеризует готовность инвестора принимать риск с учетом возможной доходности финансового актива.
Источник
Семь раз отмерь, чтобы не отрезали
Как рассчитать оптимальные доли финансовых активов в портфеле, исходя из желаемого риска, и как возложить всю ответственность на Excel
Полноценная торговая система должна не только сообщать трейдеру о моменте входа и выхода, но также указывать оптимальный размер позиции в конкретный момент. Но о последнем многие часто забывают или просто не уделяют должного внимания. Многие считают, что разработки удачного торгового плана без методики управления капиталом достаточно самой по себе. Однако это не так, и самые большие убытки, которые случались на бирже, связаны именно с отсутствием адекватного представления о размере позиции.
Часто инвесторы руководствуются каким-то субъективным мнением о том, сколько денег надо выделить под покупку той или иной акции. Но на самом деле размер позиции в каждой конкретной сделке четко связан с величиной риска, которую мы готовы принять по отношению к сумме нашего депозита. Чтобы не быть голословными, в редакции журнала D’ решили создать свой «портфель» и рассчитать оптимальные размеры позиции для каждой входящей в него акции с учетом ожидаемого риска и доходности.
Больше акций — меньше риск, или Красота матобоснования
Суть нашего подхода — обычная портфельная теория, начало которой положили работы Гарри Марковица. При этом специально для скептиков, которые не верят в экономику как в науку в принципе, добавим, что в основе портфельной теории лежит довольно простое и изящное математическое обоснование, а применить ее под силу обычному старшекласснику.
Итак, если вы представляете себе набор акций, из которых хотели бы сформировать свой инвестиционный портфель, то для каждой бумаги следует рассчитать оптимальные доли. При этом нужно учитывать такие параметры, как ожидаемая доходность, ожидаемый уровень риска и корреляция. Рассмотрим их более подробно.
Ожидаемая доходность акции рассчитывается на основе ее исторической доходности за предыдущее периоды и равна их среднему арифметическому. В таблице 1 представлена доходность условного актива (или акции) за пять лет. Среднее арифметическое доходностей за пять лет составит 7,8%, что и будет величиной ожидаемой доходности. Для определения ожидаемой доходности всего портфеля (Ep), нужно сложить все произведения ожидаемой доходности бумаг и их долей:
где Ep — ожидаемая доходность портфеля;
ei — ожидаемая доходность i-го финансового инструмента, входящего в портфель;
Wi — доля i-го финансового инструмента в портфеле.
Очевидно, что сумма всех долей ΣWi = 1.
Иногда в качестве ожидаемой доходности акции берут величину потенциального роста (upside) из аналитических обзоров. Мы же будем действовать согласно классической портфельной теории, в которой для расчетов используются исторические значения.
Степень возможного отклонения доходности акции от ожидаемого значения определяют через дисперсию. Дисперсия показывает, насколько фактические доходности акции отклоняются от ее средней (ожидаемой) доходности. Формула, по которой вычисляется дисперсия, наверняка знакома многим еще со школы: ее использовали для определения погрешности измерений в лабораторных работах по физике. Она имеет следующий вид:
где ei — доходность акции за i-й период;
— среднее значение акции за весь рассматриваемый временной интервал;
n — количество временных периодов;
σ 2 — дисперсия доходности акции на данном временном интервале.
В качестве примера снова возьмем данные из таблицы 1 и вычислим по ним дисперсию актива за пять лет. Здесь — среднее значение доходности актива за рассматриваемый временной интервал, то есть его ожидаемая доходность, равная 7,8%. Тогда получаем:
((7 – 7,8) 2 + (–4 – 7,8) 2 + (16 – 7,8) 2 + (21 – 7,8) 2 + (–3 – 7,8) 2 ) / 5 = 99,4.
Размерность дисперсии — процент в квадрате. Это неудобно, поскольку сама доходность акции измеряется в процентах. Поэтому из дисперсии извлекают квадратный корень, получая таким образом стандартное (или среднее квадратическое) отклонение, которое в нашем случае и определяет уровень ожидаемого риска. Тогда σ для одного актива имеет вид:
К сожалению, стандартное отклонение σp всего портфеля не связано с σ каждой входящей в него акции таким простым соотношением, как в случае с ожидаемой доходностью. Для определения уровня риска портфеля вводится еще одно математическое действие — вычисление ковариации.
Ковариация показывает нам взаимосвязь доходности двух акций и бывает положительной, отрицательной и нулевой. При этом чем больше абсолютное значение ковариации, тем теснее связь между бумагами. Если ковариация положительная, то при изменении одной величины другая будет меняться в том же направлении. Если отрицательная, величины будут изменяться в противоположных направлениях. В случае нулевой ковариации (близкой к нулю) считается, что связь между случайными величинами отсутствует. Рассмотрим ковариацию между двумя акциями A и B. Формула для ее вычисления имеет следующий вид:
где eAi — доходность акции А за i-й период,
eBi — доходность акции В за i-й период,
, — средние (ожидаемые) доходности акций А и B за весь рассматриваемый временной интервал.
Определим ковариацию двух акций (см. таблицу 2). Ожидаемая доходность за пятилетний временной интервал у акции А равна 6%, а у В — 12,4%. Тогда получаем:
((10 – 6) х (14 – 12,4) + (–12 – 6) х (3 – 12,4) + (23 – 6) х (17 – 12,4) + (11 – 6) х (22 – 12,4) + (–2 – 6) х (6 – 12,4)) / 5 = 70,6%.
Если в портфеле имеется более двух бумаг, то нам нужно вычислить ковариацию для всех пар. При этом можно заметить, что COV(A, B) = COV(B, A) и COV(A, A) = σ 2 A.
Итоговая формула σp для портфеля из N активов будет записываться в матричной форме (за счет множества значений ковариаций), однако мы не будем углубляться в сложности, тем более что для наших целей этого и не требуется. Но для портфеля из двух акций выражение для σp имеет достаточно простой вид:
где WА, WB — доли акций А и В в портфеле;
σA, σB — стандартное отклонение акций А и В;
COV(A, B) — ковариация доходностей акций А и B.
Из формулы видно, что при фиксированных значениях стандартных отклонений акций и ковариации на дисперсию портфеля (σ 2 p) может повлиять только распределение долей между А и В. Таким образом, имея некоторый набор акций в портфеле, всегда можно получить минимальный уровень риска для данной совокупности активов, просто меняя их доли в портфеле. Теперь, понимая эту важную вещь, попробуем подобрать такие доли для нашего портфеля, чтобы минимизировать возможные убытки в будущем.
Оптимизация: исполнима
На 8 ноября 2010 года «портфель» журнала D’ включал акции 25 эмитентов. Рассчитаем для каждой из них оптимальную долю, исходя из критерия максимальной доходности при заданном уровне риска.
Все расчеты будут проводиться в программе Excel. Временной интервал возьмем с января по октябрь 2010 года, расчетный период — один месяц. Исходя из цен закрытия на конец периода, рассчитаем доходности за каждый месяц. В таблице 3 представлены результаты вычислений (все значения в долях единицы). При этом нужно отметить, что рассчитанная ожидаемая доходность является средней за месяц, и если мы хотим привести ее к годовой, то полученное значение следует умножить на 12 (количество месяцев в году). Дисперсия вычисляется с помощью встроенной функции Excel — ДИСПР, и итоговое значение аналогичным образом умножается на 12.
Наиболее сложный момент — нахождение матрицы ковариации, которая содержит весь набор парных ковариаций между активами портфеля. Имея 25 акций, нам нужно рассчитать 300 ковариаций, не считая 25 дисперсий (которые являются диагональными элементами матрицы ковариации). Рассчитывать это вручную — занятие явно не из приятных, поэтому воспользуемся возможностями Excel. В меню «Сервис» выбираем «Анализ данных». В появившемся окне нам предлагаются различные математические инструменты анализа данных, среди которых можно найти и ковариацию. После ее вызова должно появиться окно. В поле «Входной интервал» нужно ввести рассчитанные ранее месячные доходности (см. таблицу 3).
Следующий момент — «Группировка». На нее следует обратить особое внимание, поскольку именно она определяет набор данных, по которым рассчитывается ковариация. В нашем случае она будет располагаться по строкам, поскольку периоды временного интервала у нас расположены горизонтально. В подразделе «Параметры вывода» можно воспользоваться любым способом вывода результатов, но, если размер матрицы будет достаточно большим, как в нашем случае, лучше выбрать пункт «Новый рабочий лист». В результате мы должны получить матрицу ковариаций размером 25 x 25. Как мы отмечали ранее, COV(A, B) = COV(B, A). Значит, полученная матрица будет симметричной, поэтому Excel не заполнит ячейки выше диагонали, на которой, в свою очередь, расположены значения дисперсий доходности акций COV(A, A) = σ 2 A.
Последний шаг в вычислении дисперсии портфеля — перемножение строки со значениями долей акций в портфеле на матрицу ковариации с последующим умножением результата на столбец с долями. Поскольку мы еще не знаем, какие доли приписывать каждой акции, то распределим их пока равномерно по портфелю, то есть вес всех акций в портфеле будет одинаков и составит 1/25 = 0,04. Теперь займемся умножением. Сначала перемножается строка с долями на матрицу ковариаций с помощью команды МУМНЖ(). Результатом умножения будет строка, которую нужно умножить на столбец долейс помощью той же команды МУМНЖ(). Полученное наконец число и есть дисперсия нашего портфеля. Для вычисления стандартного отклонения, которое в данном случае является уровнем риска портфеля, умножим дисперсию на 12 и извлечем из полученного значения квадратный корень.
Сколько вешать в граммах
Вот теперь можно решить, собственно, нашу основную задачу — вычислить оптимальные доли акций в портфеле. Снова воспользуемся возможностями Excel и в меню «Сервис» выберем «Поиск решения». В подразделе «Установить целевую ячейку» прописываем адрес ячейки, где у нас рассчитывается ожидаемая доходность портфеля. В нашем случае это ячейка D27 . Следующий подраздел определяет значение целевой ячейки. Поскольку мы хотим иметь максимальную доходность при любых условиях, нужно выбрать пункт «Максимальное значение». В подразделе «Изменяя ячейки» вводим диапазон ячеек, где прописаны доли нашего портфеля — В2–В26. И последнее поле — «Ограничения», где мы указываем дополнительные условия. В нашем случае это значения долей в интервале от 0,001 до 0,006 включительно, сумма долей должна быть равна единице (обязательное условие, если мы не берем «плечи» и распределяем по активам все деньги полностью), и последнее — назначение верхней границы приемлемого уровня риска. Это максимальное значение просадки портфеля в процентах, величину которой каждый выбирает самостоятельно (исходя из собственных торговых предпочтений).
Вообще-то большинство акций имеют однонаправленную корреляцию (особенно это касается российского фондового рынка), а также собственный уровень риска. В результате этого значение минимальной просадки портфеля естественным образом ограничивается снизу. Этот минимальный размер мы находим эмпирически, то есть методом подбора.
После того как все параметры введены, можно нажать кнопку «Выполнить», и в столбце с весами появятся новые значения удельных весов акций. Таким образом, каждый раз фиксируя определенное значение допустимого уровня риска (стандартного отклонения), мы получаем портфель с таким распределением долей, при котором его доходность максимальна.
Если повторить решение задачи для различных уровней риска, мы получим целый набор значений ожидаемой доходности оптимального портфеля. Эти данные позволяют построить так называемую эффективную границу, или границу Марковица. На графике 1 изображен эскиз этой кривой (14 точек), и можно заметить, что минимальный уровень риска нашего портфеля составляет около 18%. При этом ожидаемая доходность будет порядка 41% годовых. При увеличении уровня риска доходность также возрастает. В таблице 4 представлен итоговый портфель с рассчитанными оптимальными долями, соответствующими минимальному уровню риска — 18%. Кроме того, рассчитаны ожидаемая годовая доходность каждой акции и доходность соответствующей доли в портфеле.
Все, о чем мы говорили выше, относится к так называемой стратегии buy & hold, а полученная в итоге доходность была бы таковой, если бы мы сформировали портфель в начале этого года. Тем не менее эти результаты дают некий ориентир, на который можно полагаться в своих ожиданиях. Рассмотренный пример позволяет понять, насколько важно в своем торговом методе иметь систему управления капиталом. Если вы еще не используете ее, то ради эксперимента попробуйте торговать вместе с ней. Разница в результатах будет заметна практически сразу.
Источник