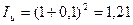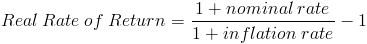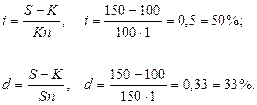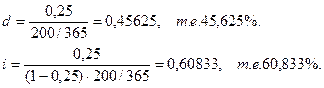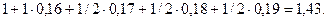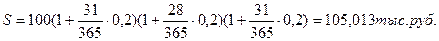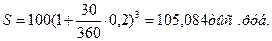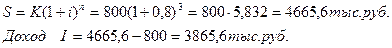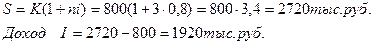Как найти реальную доходность операции

Определение реальной доходности операции в условиях инфляции

Дата добавления: 2015-01-16 ; просмотров: 3939 ; Нарушение авторских прав

В условиях инфляции важно также уметь определять реальную доходность операции, полученную при сложившемся уровне инфляции.

Из формулы (2.6) можно получить формулу, позволяющую определить реальную доходность финансовой операции, когда задан уровень инфляции и простая ставка процентов, учитывающая инфляцию.

. (2.12)

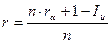
Пример 2.3.Срок операции составил полгода. При этом уровень инфляции в этот период был 2% в месяц. Определить реальную доходность такой операции, если простая ссудная ставка была 20% годовых.

За полгода индекс инфляции составил:

.

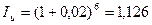
Тогда по формуле (2.12)

( –5,2%).

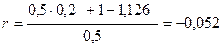
Проведенные расчеты показывают, что реально такая операция принесет убыток 5,2%.

Из формулы (2.8) получаем аналогичную формулу для случая сложных процентов:

. (2.13)

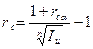
Пример 2.4.Клиент банка внес деньги на депозит сроком 2 года. Какова реальная доходность такого вложения под сложную ссудную ставку 15%, если уровень инфляции составит 10% в год.

Индекс инфляции составит за два года:

Тогда для определения реальной доходности используем формулу (2.13)

(4,5%).

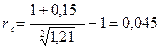
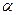
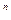
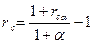
Подставив в формулу (2.13) вместо индекса инфляции выражение (1+ ) ,получим простую формулу

, (2.14)

отражающую несколько очевидных соображений:

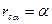
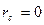
-если (доходность вложений и уровень инфляции равны), то , т. е. весь доход поглощается инфляцией;

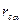
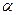
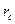
-если (доходность вложений выше уровня инфляции), то >0, т.е. происходит реальный прирост вложенного капитала.

Аналогично определяют формулы для учетных ставок.

Источник

Как правильно считать реальную доходность с учетом инфляции?

Автор: Алексей Мартынов · Опубликовано 03.07.2015 · Обновлено 02.12.2018

Наверно все знают, что реальная доходность — это доходность за вычетом инфляции. Все дорожает — продукты, товары, услуги. По данным Росстата за последние 15 лет цены выросли в 5 раз. Это означает, что покупательная способность денег, просто лежавших все это время в тумбочке уменьшилась в 5 раз, раньше могли купить 5 яблок, теперь 1.

Чтобы хоть как-то сохранить покупательную способность своих денег, люди их вкладывают в различные финансовые инструменты: чаще всего это депозиты, валюта, недвижимость. Более продвинутые используют, акции, ПИФы, облигации, драгметаллы. С одной стороны сумма вложений растет, с другой происходит их обесценивание из-за инфляции. Если из номинальной ставки доходности вычесть ставку инфляции, получится реальная доходность. Она может быть положительной или отрицательной. Если доходность положительная, ваши вложения приумножились в реальном выражении, то есть вы можете купить больше яблок, если отрицательная — обесценились.

Большинство инвесторов считают реальную доходность по простой формуле:

Но данный способ неточен. Приведу пример: возьмем 200 рублей и положим их на депозит на 15 лет со ставкой 12% годовых. Инфляция за этот период 7% в год. Если считать реальную доходность по простой формуле, то получится 12-7=5%. Проверим этот результат, посчитав на пальцах.

За 15 лет при ставке 12% годовых 200 рублей превратятся в 200*(1+0,12)^15=1094,71. Цены за это время вырастут в (1+0,07)^15=2,76 раз. Чтобы посчитать реальную доходность в рублях делим сумму на депозите на коэффициент инфляции 1094,71/2,76=396,63. Теперь, чтобы перевести реальную доходность в проценты считаем (396,63/200)^1/15 -1 *100% = 4,67%. Это отличается от 5%, то есть проверка показывает, что расчет реальной доходности «простым» способом не точен.
Чтобы правильно рассчитать реальную доходность, нужно применять формулу:

Real Rate of Return — реальная доходность
nominal rate — номинальная ставка доходности
inflation rate — инфляция

Проверяем:
(1+0,12)/(1+0,07)-1 * 100%=4,67% Сходится, значит формула верная.

Еще одна формула, которая дает тот же результат, выглядит так:

Источник

Формулы доходности финансовых операций

Если в формулах наращения по процентной и учетной ставке принять срок n = 1 году, то получим, что

.

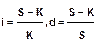
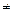
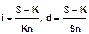
Если n1 году, .

Эти формулы принято называть формулами доходности или эффективности по простой ставке процентов и учетной ставке соответственно.

Предприятие получило кредит на 1 год в размере 100 млн. с условием возврата 150 млн.

Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок.

К = 100 млн., S = 150 млн., n = 1 год. I = ?, d = ?

Решение:

Дисконтная ставка всегда меньше процентной, ибо она учитывает время более жестко.

Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли (или процента) от суммы погасительного платежа. Таким образом, уровень процентной ставки задается в неявном виде. Выведем формулы, с помощью которых можно вычислить значения этих ставок.

Пусть S- размер погасительного платежа (сумма ссуды к концу срока),

d_n – доля этого платежа, определяющая величину дисконта за весь срок ссуды.

К = S(1 – d_n) – реально выдаваемая ссуда в момент заключения договора.

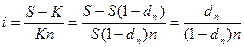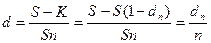Задача 7.

Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней.

Простые переменные ставки

В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.

Если i₁, i₂,… i_k – последовательные во времени простые ставки,

а n_1, n_2,… n_k – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:

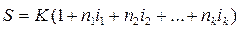Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.

Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года.

Множитель наращения =

Иначе, за 2,5 года начальный капитал увеличился в 1,43 раза.

Реинвестирование

В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!)

В этом случае наращенная сумма для всего срока составит:

(14) k – количество реинвестиций.

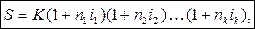
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:

, k – количество реинвестиций.

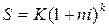
Задача 9.

Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам.

По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам.

По точным процентам:

(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!)

По банковским процентам при условии, что в каждом месяце по 30 дней:

Модуль 2. Сложные проценты

Наращение по сложным процентам

В среднесрочных и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты.

Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов.

Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид

(1) , где i — годовая (номинальная) процентная ставка, n — число лет начисления,

— множитель наращения по сложным процентам.

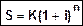
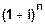
Задача 1.

Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

2. Простые проценты:

За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам.

Задача 2.

Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

Источник

Считаем доходность инвестиций по Фишеру: зачем инвестору макроэкономика?

Ирвинг Фишер — американский экономист, представитель неоклассического направления в экономической науке. Родился 27 февраля 1867 года в Согертис, шт. Нью-Йорк. Он внес большой вклад в создание теории денег, а так же вывел «уравнение Фишера» и «уравнение обмена».

Его труды были взяты за основу современных методик для расчета уровня инфляции. Кроме того, они во многом помогли понять закономерности явления инфляции и ценообразования.

Полная и упрощенная формула Фишера

В упрощенном виде формула будет выглядит так:

i = r + π

• i — номинальная процентная ставка;
• r — реальная процентная ставка;
• π — темп инфляции.

Данная запись является приближенной. Чем меньше значения r и π, тем точнее выполняется это уравнение.

Более точной будет является такая запись:

r = (1 + i)/(1 + π) — 1 = (i — π)/(1 + π)

Количественная теория денег

Количественная теория денег — это экономическая теория, которая изучает воздействие денег на экономическую систему.

В соответствии с моделью, выдвинутой Ирвингом Фишером, государство должно регулировать объем денежных масс в экономике, чтобы избежать их недостатка или чрезмерного количества.

Согласно этой теории, явление инфляции возникает по причине несоблюдении этих принципов.

Недостаточное или чрезмерное количество денежной массы в обороте влечет за собой рост темпа инфляции.

В свою очередь рост инфляции предполагает рост номинальной процентной ставки.

• Номинальнаяпроцентная ставка отражает только текущую прибыль от вкладов без учета инфляции.
• Реальнаяпроцентная ставка — это номинальная ставка процента за вычетом ожидаемого уровня инфляции.

Уравнение Фишера описывает соотношения возникающие между этими двумя показателями и уровнем инфляции.

Видео

Советуем посмотреть данное видео, чтобы лучше разобраться в теории:

Как применять для расчета доходности инвестиции

Предположим, что вы делаете вклад в размере 10 000, номинальная процентная ставка составляет 10%, а уровень инфляции 5% в год. В таком случае реальная процентная ставка составит 10% — 5% = 5%. Таким образом, реальная процентная ставка тем меньше, чем выше уровень инфляции.

Именно эту ставку стоит учитывать, чтобы рассчитать количество денег, которое данный вклад принесет вам в будущем.

Типы начисления процентов

Как правило, начисления процентов прибыли происходит в соответствии с формулой сложного процента.

Сложный процент — это метод начисления процентов прибыли, при котором они прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.

Краткая запись формулы сложных процентов выглядит так:

K = X * (1 + %) n

• K — итоговая сумма;
• X — начальная сумма;
• % — процентное значение выплат;
• n — количество периодов.

При этом, реальный процент, который вы получите сделав вклад под сложные проценты, будет тем меньше, чем выше уровень инфляции.

При этом для любого вида инвестиций имеет смысл рассчитывать эффективную (реальную) процентную ставку: по своей сути это процент от начального вклада, который инвестор получит в конце срока инвестирования. Проще говоря, это отношение полученной суммы к первоначально инвестированной сумме.

r(ef) = (P_n — P)/P

• r_ef — эффективный процент;
• Pn — итоговая сумма;
• P — начальный вклад.

Используя формулу сложных процентов получим:

r_ef = (1 + r/m) m — 1

Где m — количество начислений за период.

Международный эффект Фишера

Международный эффект Фишера — это теория обменного курса, выдвинутая Ирвингом Фишером. Суть этой модели заключается в расчете настоящих и будущих номинальных процентных ставок для того, чтобы определять динамику изменений курса обмена валют. Данная теория работает в чистом виде в том случае, если капитал свободно движется между государствами, валюты которых могут быть соотнесены друг с другом по стоимости.

Анализируя прецеденты роста инфляции в разных странах, Фишер заметил закономерность в том, что реальные процентные ставки, несмотря на рост количества денег не увеличиваются. Данное явление объясняется тем, что оба параметра со временем уравновешиваются посредством рыночного арбитража. Этот баланс соблюдается по той причине, что процентная ставка устанавливается с учетом риска инфляции и рыночных прогнозах по валютной паре. Это явление получило название эффект Фишера .

Экстраполировав эту теории на международные экономические отношения, Ирвинг Фишер сделал вывод, что изменение номинальных процентных ставок оказывает непосредственное влияние на подорожание или удешевление валюты.

Данная модель так и не была протестирована в реальных условиях. Основным её недостатком принято считать необходимость выполнения паритета покупательной способности (одинаковая стоимость аналогичных товаров в разных странах) для точного прогнозирования. И, к тому же, неизвестно, можно ли использовать международный эффект Фишера в современных условиях, с учетом колеблющихся курсов валют.

Прогнозирование инфляции

Явление инфляции заключается чрезмерном количестве, обращающихся в стране денег, что ведет к их обесцениванию.

Классификация инфляции происходит по признакам:

Равномерности — зависимости темпа инфляции от времени.

Однородности — распространения влияния на все товары и ресурсы.

Прогнозирование инфляции рассчитывается с помощью индекса инфляции и скрытой инфляции.

Основными факторами при прогнозировании инфляции являются:

• изменение курса валют;
• увеличение количества денег;
• изменение процентных ставок;

Также распространенным метод является расчет уровня инфляции на основе дефлятора ВВП. Для прогнозирования в этой методике фиксируют такие изменения в экономике:

• изменение прибыли;
• изменение выплат потребителям;
• изменение импортных и экспортных цен;
• изменение ставок.

Расчет доходности инвестиций с учетом уровня инфляции и без него

Доходностью инвестиций принято считать процентное отношение полученной прибыли к сумме начального взноса.

Формула доходности без учета инфляции будет выглядеть следующим образом:

X = ((P_n — P) / P )*100%

• X — доходность;
• P_n — итоговая сумма;
• P — начальный взнос;

В этом виде итоговая доходность рассчитывается без учета потраченного времени.

Для того, чтобы рассчитать доходность в процентах годовых, необходимо воспользоваться следующей формулой:

X_t = ((P_n — P) / P ) * (365 / T) * 100%

Где T — количество дней владения активом.

Оба способа не учитывают влияния инфляции на доходность.

Доходность с учетом инфляции (реальную доходность) следует рассчитывать по формуле:

R = (1 + X) / (1 + i) — 1

• R — реальная доходность;
• X — номинальная ставка доходности;
• i — инфляция.

Исходя из модели Фишера, можно сделать один главный вывод: инфляция не приносит доходов.

Повышение номинальной ставки вследствие инфляции никогда не будет больше, чем количество денег вложенных, которое обесценилось. Кроме того, высокий темп роста инфляции предполагает значительные риски для банков, и компенсация этих рисков лежит на плечах вкладчиков.

Применение формулы Фишера в международных инвестициях

Как можно заметить, в приведенных выше формулах и примерах, уровень высокий инфляции всегда снижает доходность инвестиций, при неизменной номинальной ставке.

Таким образом, основным критерием надежности инвестиции является не объем выплат в процентном выражении, а целевой уровень инфляции.

Подтверждением тому служит рейтинг стран, в которые поступает больше всего инвестиций. Первые места в нем занимают Китай и США. Рост инфляция в этих странах за последние 5 лет не превышал отметку в 3%.

Описание Российского инвестиционного рынка посредством формулы Фишера

Приведенная выше модель четко прослеживается на примере инвестиционного рынка РФ.

Падение инфляции в 2011-2013 году с 8.78% до 6.5% привело к повышению иностранных инвестиций: в 2008-2009 году они не превышали 43 млдр. долларов в год, а к 2013 достигли отметки в 70 млдр. долларов.

Резкое же повышение инфляции 2014-2015 привело к снижению иностранных инвестиций до исторического минимума. За эти два года сумма вложений в экономику России составила всего 29 млдр. долларов.

На данный момент, инфляция в России упала до 2.09%, что уже привело к притоку новых вложений от инвесторов.

В данном примере можно заметить, что в вопросах международного инвестирования основным параметром является именно реальная процентная ставка, расчет которой происходит по формуле Фишера.

Как рассчитывается индекс инфляции товаров и услуг

Индекс инфляции или индекс потребительских цен — это показатель, который отражает изменение цен товаров и услуг, покупаемых населением.

Численно индекс инфляции представляет собой отношение цен на товары в отчетный период к ценам на аналогичные товары базисного периода.

• i_p — индекс инфляции;
• p₁ — цены на товары в отчетный период;
• p₂ — цены на товары в базисный период.

Проще говоря, индекс инфляции указывает на то, во сколько раз изменились цены за определенный промежуток времени.

Зная индекс инфляции, можно сделать вывод о динамике инфляции. Если индекс инфляции принимает значения больше единицы, то цены растут, а значит растет и инфляция. Индекс инфляции меньше единицы — инфляция принимает отрицательные значения.

Для прогнозирования изменений индекса инфляции используют следующие способы:

Формула Ласпейреса:

• I_L — индекс Ласпейреса;
• Числитель — суммарная стоимость товаров проданных в предыдущем периоде по ценам отчетного периода;
• Знаменатель — реальная стоимость товаров в предыдущем периоде.

Инфляции, при повышении цен, дается высокая оценка, а при их падении — заниженная.

Индекс Пааше:

Числитель — фактическая стоимость продукции отчетного периода;

Знаменатель — фактическая стоимость продукции отчетного периода.

Идеальный индекс цен Фишера:

Учет инфляции при расчете инвестиционного проекта

Учёт инфляции в таких инвестициях играет ключевую роль. Инфляции может повлиять на реализацию проекта в двух аспектах:

• В натуральном выражении — то есть, повлечь за собой изменение плана реализации проекта.
• В денежном выражении — то есть, повлиять на итоговою доходность проекта.

Способы влияния на инвестиционный проект в случае повышения инфляции:

1. Изменение валютных потоков в зависимости от инфляции;
2. Учет инфляционной премии в ставке дисконтирования.

Анализ уровня инфляции и её возможного влияния на инвестиционный проект требуют следующих мер:

• учет потребительского индекса;
• прогнозирование изменения индекса инфляции;
• прогнозирование изменения дохода населения ;
• прогнозирование объема денежных сборов.

Формула Фишера для расчета зависимости стоимости товаров от количества денег

В общем виде формула Фишера для расчета зависимости стоимости товаров от количества денег имеет следующую запись:

MV = PQ

• М — объем денежных масс в обороте;
• V — частота, с которой деньги используются;
• Р — уровень стоимости товаров;
• Q — количеств товаров в обороте.

Преобразовав эту запись, можно выразить уровень цен: P=MV/Q.

Главным выводом из данной формулы является обратная пропорциональность между стоимостью денег и их количеством. Таким образом, для нормального товарообращения в пределах государства, требуется контроль количества денег, находящихся в обороте. Повышения количества товаров и цен на них требует увеличения количества денег, а, в случае уменьшения этих показателей, следует уменьшать денежную массу. Такого рода регулирование объема денег в обращении возлагается на государственный аппарат.

Формула Фишера в применении к монопольному и конкурентному ценообразованию

Чистая монополия прежде всего предполагает, что один производитель полностью контролирует рынок и совершенной информированностью о его состоянии. Основной целью монополии является максимальная прибыль при минимальных расходах. Монополия всегда устанавливает цену выше значения предельных затрат, а объем выпуска ниже, чем в условиях совершенной конкуренции.

Присутствие на рынке производителя-монополиста как правило имеет серьезные экономические последствия: потребитель тратит больше денег, чем в условиях жесткой конкуренции, при этом рост цен происходит вместе с ростом индекса инфляции.

Если изменение этих параметров учесть в формуле Фишера, то мы получим увеличение денежной массы и постоянное уменьшение количества обращающихся товаров. Такое положение приводит экономику к порочному циклу, в котором увеличение уровня инфляции ведет к увеличению только к увеличению цен, что в конце концов ещё больше стимулирует темп роста инфляции.

Конкурентный же рынок, в свою очередь, реагирует на повышение индекса инфляции совершенно другим образом. Рыночный арбитраж приводит к соответствию цен конъюктуре. Таким образом, конкуренция препятствует чрезмерному увеличению денежной массы в обороте.

Пример связи изменения процентных ставок с уровнем инфляции для России

На примере России, можно заметить прямую зависимость процентных ставок по вкладам от инфляции

Год	Процентная ставка, %	Инфляция, %
2017	9.75-7.75	2.09
2016	10.5-10.0	5.38
2015	15.0-11.0	12.91
2014	7.0-17.0	11.36

Таким образом видно, что нестабильность внешних условий и увеличение волатильности на финансовых рынках заставляет Центральный Банк снижать ставки, при повышении инфляции.

Источник