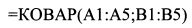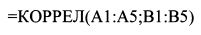Ковариация
Ковариацией $cov\left(X,\ Y\right)$ случайных величин $X$ и $Y$ называется математическое ожидание произведения случайных величин $X-M\left(X\right)$ и $Y-M\left(Y\right)$, то есть:
Бывает удобно вычислять ковариацию случайных величин $X$ и $Y$ по следующей формуле:
которая может быть получена из первой формулы, используя свойства математического ожидания. Перечислим основные свойства ковариации.
1. Ковариация случайной величины с самой собой есть ее дисперсия.
2. Ковариация симметрична.
$$cov\left(X,\ Y\right)=cov\left(Y,\ X\right).$$
3. Если случайные величины $X$ и $Y$ независимы, то:
4. Постоянный множитель можно выносить за знак ковариации.
$$cov\left(cX,\ Y\right)=cov\left(X,\ cY\right)=c\cdot cov\left(X,\ Y\right).$$
5. Ковариация не изменится, если к одной из случайных величин (или двум сразу) прибавить постоянную величину:
$$cov\left(X+c,\ Y\right)=cov\left(X,\ Y+c\right)=cov\left(X+x,\ Y+c\right)=cov\left(X,\ Y\right).$$
6. $cov\left(aX+b,\ cY+d\right)=ac\cdot cov\left(X,\ Y\right)$.
8. $\left|cov\left(X,\ Y\right)\right|=\sqrt
9. Дисперсия суммы (разности) случайных величин равна сумме их дисперсий плюс (минус) удвоенная ковариация этих случайных величин:
$$D\left(X\pm Y\right)=D\left(X\right)+D\left(Y\right)\pm 2cov\left(X,\ Y\right).$$
Пример 1. Дана корреляционная таблица случайного вектора $\left(X,\ Y\right)$. Вычислить ковариацию $cov\left(X,\ Y\right)$.
$\begin
\hline
X\backslash Y & -6 & 0 & 3 \\
\hline
-2 & 0,1 & 0 & 0,2 \\
\hline
0 & 0,05 & p_ <22>& 0 \\
\hline
1 & 0 & 0,2 & 0,05 \\
\hline
7 & 0,1 & 0 & 0,1 \\
\hline
\end
События $\left(X=x_i,\ Y=y_j\right)$ образуют полную группу событий, поэтому сумма всех вероятностей $p_
$\begin
\hline
X\backslash Y & -6 & 0 & 3 \\
\hline
-2 & 0,1 & 0 & 0,2 \\
\hline
0 & 0,05 & 0,2 & 0 \\
\hline
1 & 0 & 0,2 & 0,05 \\
\hline
7 & 0,1 & 0 & 0,1 \\
\hline
\end
Пользуясь формулой $p_ =\sum _
$\begin
\hline
X & -2 & 0 & 1 & 7 \\
\hline
p_i & 0,3 & 0,25 & 0,25 & 0,2 \\
\hline
\end
$$M\left(X\right)=\sum^n_
Пользуясь формулой $q_
$$M\left(Y\right)=\sum^n_
Поскольку $P\left(X=-2,\ Y=-6\right)=0,1\ne 0,3\cdot 0,25$, то случайные величины $X,\ Y$ являются зависимыми.
Определим ковариацию $cov\ \left(X,\ Y\right)$ случайных величин $X,\ Y$ по формуле $cov\left(X,\ Y\right)=M\left(XY\right)-M\left(X\right)M\left(Y\right)$. Математическое ожидание произведения случайных величин $X,\ Y$ равно:
$$M\left(XY\right)=\sum_
Тогда $cov\left(X,\ Y\right)=M\left(XY\right)-M\left(X\right)M\left(Y\right)=-1,95-1,05\cdot \left(-0,45\right)=-1,4775.$ Если случайные величины независимы, то их ковариации равна нулю. В нашем случае $cov(X,Y)\ne 0$.
Корреляция
Коэффициентом корреляции случайных величин $X$ и $Y$ называется число:
Перечислим основные свойства коэффициента корреляции.
1. $\rho \left(X,\ X\right)=1$.
2. $\rho \left(X,\ Y\right)=\rho \left(Y,\ X\right)$.
3. $\rho \left(X,\ Y\right)=0$ для независимых случайных величин $X$ и $Y$.
5. $\left|\rho \left(X,\ Y\right)\right|\le 1$.
6. $\left|\rho \left(X,\ Y\right)\right|=1\Leftrightarrow Y=aX+b$.
Ранее было сказано, что коэффициент корреляции $\rho \left(X,\ Y\right)$ отражает степень линейной зависимости между двумя случайными величинами $X$ и $Y$.
При $\rho \left(X,\ Y\right)>0$ можно сделать вывод о том, что с ростом случайной величины $X$ случайная величина $Y$ имеет тенденцию к увеличению. Это называется положительной корреляционной зависимостью. Например, рост и вес человека связаны положительной корреляционной зависимостью.
При $\rho \left(X,\ Y\right) Да Нет
При копировании материала с сайта, обратная ссылка обязательна!
Источник
1.2.4. Использование программы Excel для расчета ковариации и коэффициента корреляции доходностей ценных бумаг
Рассмотрим технику расчета ковариации и корреляции доходностей бумаг на примере.
Доходность бумаги X за пять лет составила соответственно 20%, 25%, 22%, 28%, 24%. Доходность бумаги F: 24%, 28%, 25%, 27%, 23%. Определить ковариацию доходностей бумаг.
Приведем решение задачи двумя способами.
а) Печатаем в хронологическом порядке в ячейках с Al no A5 значения доходности бумаги X, а в ячейках с В1 по В5 — доходности бумаги F. Решение получим в ячейке С1, поэтому наводим на нее курсор и щелкаем мышью. Печатаем в ячейке С1 формулу:
и нажимаем клавишу Enter. В ячейке С1 появилось решение задачи — цифра 3,08, т.е. выборочная ковариация для нашего примера.
б) Ковариацию можно рассчитать с помощью программы «Мастер функций». Для этого наводим курсор на значок А на панели инструментов и щелкаем мышью. Появилось окно «Мастер функций». В левом поле («Категория») наводим курсор на строку «Статистические» и щелкаем мышью. Строка высветилась синим цветом, а в правом поле окна («Функция») появился перечень статистических функций. Наводим курсор на строку «КОВАР» и щелкаем левой клавишей мыши. Строка высветилась синим цветом. Наводим курсор на кнопку ОК и щелкаем мышью. Появилось окно «КОВАР». В окне две строки, которые называются «Массив 1» и «Массив 2». В первую строку заносим номера ячеек с А1 по А5. Для этого наводим курсор на знак 3, расположенный с правой стороны первой строки и щелкаем мышью. Окно «КОВАР» превратилось в поле первой строки. Наводим курсор на ячейку А1, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, доводим курсор вниз до ячейки А5 и отпускаем клавишу. В поле строки появилась запись А1:А5. Вновь наводим курсор на знак . и щелкаем мышью. Появилось развернутое окно «КОВАР». Заносим номера ячеек с Bl no B5 во вторую строку. Для этого наводим курсор на знак 5J во второй строке и щелкаем мышью. Наводим курсор на ячейку В1, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, доводим курсор вниз до ячейки В5, отпускаем клавишу. В поле строки появилась запись В1:В5. Наводим курсор на кнопку 3| и щелкаем мышью. Появилось развернутое окно «КОВАР». Наводим курсор на кнопку ОК и щелкаем мышью. В ячейке С1 появилась цифра 3,08.
Определить коэффициент корреляции доходностей бумаг для условий примера 1. Решение. Приведем решение задачи двумя способами.
а) Печатаем в хронологическом порядке в ячейках с Al no A5 значения доходности бумаги X, а в ячейках с В1 по В5 — доходности бумаги F. Решение получим в ячейке С1, поэтому наводим на нее курсор и щелкаем мышью. Печатаем в ячейке С1 формулу:
и нажимаем клавишу Enter. В ячейке С1 появилось решение задачи — цифра 0,612114.
б) Корреляцию можно рассчитать с помощью программы «Мастер функций». Для этого выбираем курсором на панели инструментов значок л» и щелкаем мышью. Появилось окно «Мастер функций». В левом поле («Категория») выбираем курсором строку «Статистические» и щелкаем мышью. В правом поле окна («Функция») появился перечень статистических функций. Выбираем курсором строку «КОРРЕЛ» и щелкаем мышью. Строка высветилась синим цветом. Наводим курсор на кнопку ОК и щелкаем мышью. Появилось окно «КОРРЕЛ». В окне две строки, которые называются «Массив 1» и «Массив 2». В первую строку заносим номера ячеек с Al no A5. Для этого наводим курсор на знак ЗР справа от первой строки и щелкаем мышью. Окно «КОРРЕЛ» превратилось в поле первой строки. Наводим курсор на ячейку А1, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, проводим курсор вниз до ячейки А5 и отпускаем клавишу. В поле строки появилась запись А1:А5. Вновь наводим курсор на знак Щ и щелкаем мышью. Появилось развернутое окно «КОРРЕЛ». Заносим номера ячеек с Bl no B5 во вторую строку. Для этого наводим курсор на знак Ш во второй строке и щелкаем мышью. Наводим курсор на ячейку В1, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, доводим курсор вниз до ячейки В5, отпускаем клавишу. В поле строки появилась запись В1:В5. Наводим курсор на кнопку Щ и щелкаем мы шью. Появилось развернутое окно «КОРРЕЛ». Наводим курсор на кнопку ОК и щелкаем мышью. В ячейке С1 появилась цифра 0,612114.
В примерах 1 и 2 мы рассчитали ковариацию и корреляцию доходностей двух бумаг в портфеле. Если в портфель входит большее количество бумаг, то ковариации и корреляции их доходностей можно рассчитывать попарно изложенным выше способом, однако это трудоемкий вариант решения задачи. В Excel имеется специальный пакет «Анализ данных», который позволяет быстро решить такую задачу для большого количества бумаг. Рассмотрим расчет ковариации и корреляций с его помощью.
Важно: актуальное предложение по поводу компенсации до 100% комиссии, взимаемой Вашим брокером.


«Пакет анализа» может быть не установлен. Тогда его необходимо установить. Для этого наводим курсор на меню «Сервис» и щелкаем левой клавишей мыши. Появилось выпадающее меню. Курсором выбираем в нем команду «Надстройки» и щелкаем левой клавишей мыши. Появилось окно диалога «Надстройки». Наводим курсор на окошко слева от строки «Пакет анализа» и щелкаем левой клавишей мыши. В окошке появился флажок (галочка). Наводим курсор на кнопку ОК и щелкаем мышью. «Пакет анализа» установлен. Рассмотрим определение ковариации и корреляций для нескольких бумаг на примере.
Пример 3. Расчет ковариации
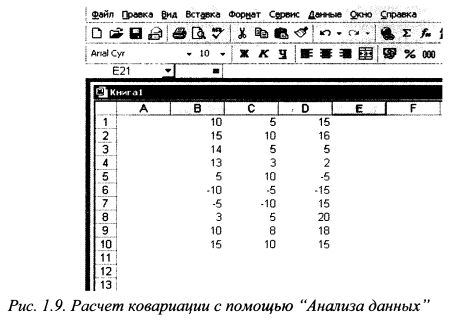
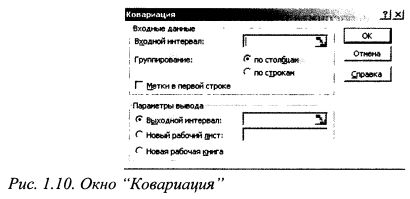
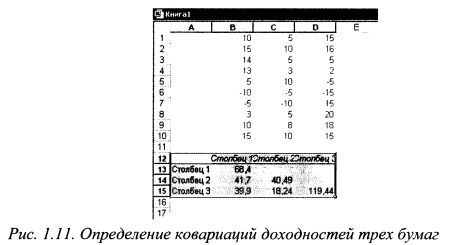
Имеется выборка данных по доходностям бумаг В, С и D за десять периодов. Печатаем значения доходности для бумаги В в ячейки от В1 до В10, бумаги С от С1 до СЮ и бумаги D от D1 до D10, как показано на рис. 1.8. Наводим курсор на меню «Сервис» и щелкаем левой клавишей мыши. Появилось выпадающее меню. Наводим курсор на строку «Анализ данных» и щелкаем левой клавишей мыши. Появилось окно» Анализ данных». Наводим курсор на строку «Ковариация» и щелкаем левой клавишей мыши. Строка высвечивается синим цветом. Наводим курсор на кнопку ОК и щелкаем мышью. Появилось окно Ковариация». (см. рис. 1.10).
Наводим курсор на знак 3 справа от поля строки «Входной интервал» и щелкаем мышью. Окно «Ковариация» свернулось в поле строки. Наводим курсор на ячейку В1, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, проводим до ячейки D10. В строке появилась запись $B$1:$D$10. Вновь наводим курсор на знак и щелкаем мышью. Появилось развернутое окно «Ковариация». Группировку данных проводим по столбцам. Поэтому, если в круглом окне слева от надписи «по столбцам» не стоит точка, то наводим на нее курсор и щелкаем левой клавишей мыши. В окне появится точка. Ниже расположена строчка «Выходной интервал». В круглом окне слева от надписи должна стоять точка. Если ее нет, то наводим курсор на данную строчку и щелкаем левой клавишей мыши. В окне появится точка. Наводим курсор на знак 3 справа от поля строки «Выходной интервал» и щелкаем мышью. Окно «Ковариация» превратилось в поле строки. В качестве начала выходного интервала возьмем ячейку А12. Поэтому наводим на нее курсор и нажимаем левую клавишу мыши. В поле строки появилась запись $А$12. Вновь наводим курсор на знак 3 и щелкаем мышью. Окно «Ковариация» развернулось. Наводим курсор на кнопку ОК и щелкаем мышью. На листе появилось решение задачи как показано на рис. 1.11. В блоке от В13 до D15 представлена ковариационная матрица. По ее диагонали, т.е. в ячейках В13, С14 и В15 расположены дисперсии соответственно бумаг В, С и D, в остальных ячейках — ковариации доходностей бумаг: в ячейке В14 ковариация доходностей бумаг В и С, в В15 – бумаг B и D,в С15 — бумаг C и D.
Пример 4. Расчет корреляций
Имеется выборка данных по доходностям трех бумаг — В, С и D — за десять периодов. Как и в задаче 3, печатаем значения доходности для бумаги В в ячейки от В1 до В10, бумаги С от С1 до С10 и бумаги D от D1 до D10 (рис. 1.9). Наводим курсор на меню «Сервис» и щелкаем левой клавишей мыши. Появилось выпадающее меню. Наводим курсор на строку «Анализ данных» и щелкаем левой клавишей мыши. Появилось окно» Анализ данных». Наводим курсор на строку «Корреляция» и щелкаем левой клавишей мыши. Строка высвечивается синим цветом. Наводим курсор на кнопку ОК и щелкаем мышью. Появилось окно корреляция (по структуре оно аналогично окну «ковариация)». Наводим курсор на знак 3 справа от поля строки «Входной интервал» и щелкаем мышью. Окно «Корреляция» свернулось в поле строки. Наводим курсор на ячейку В1, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, доводим курсор до ячейки D10. В строке появилась запись $B$1:$D$10. Вновь наводим курсор на знак и щелкаем мышью. Появилось развернутое окно «Корреляция». Группировку данных проводим по столбцам. Поэтому, если в круглом окне слева от надписи «по столбцам» не стоит точка, то наводим на нее курсор и щелкаем левой клавишей мыши. В окне появится точка. Ниже расположена строчка «Выходной интервал». В круглом окне слева от надписи должна стоять точка. Если ее нет, то наводим курсор на данную строчку и щелкаем левой клавишей мыши. В окне появится точка. Наводим курсор на знак 3 справа от поля строки «Выходной интервал» и щелкаем мышью. Окно «Корреляция» превратилось в поле строки. В качестве начала выходного интервала возьмем ячейку А12. Поэтому наводим на нее курсор и нажимаем левую клавишу мыши. В поле строки появилась запись $А$12. Вновь наводим курсор на знак 3 и щелкаем мышью. Окно «Корреляция» развернулось. Наводим курсор на кнопку ОК и щелкаем мышью. На листе появилось решение задачи как показано на рис 1.12. В блоке от В13 до D15 представлена корреляционная матрица. По ее диагонали, т.е. в ячейках В13, С14 и D15 расположены единицы, в остальных ячейках — корреляции доходностей бумаг: в ячейке В14 корреляция доходностей бумаг В и С, в В15 — бумаг B и D, в С15 — бумаг C и D.
Источник