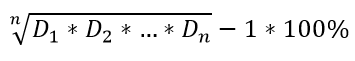- Расчет рыночной доходности
- Формула расчета рыночной доходности
- Средняя (среднегодовая) доходность: как рассчитать?
- Пример расчёта средней годовой доходности
- Калькулятор накоплений
- Как считать доходность инвестиций: формулы расчета
- Как рассчитать доходность инвестиций?
- Как считать доходность в процентах годовых?
- Как считать среднегодовую доходность
- Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Расчет рыночной доходности
Формула расчета рыночной доходности
Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.
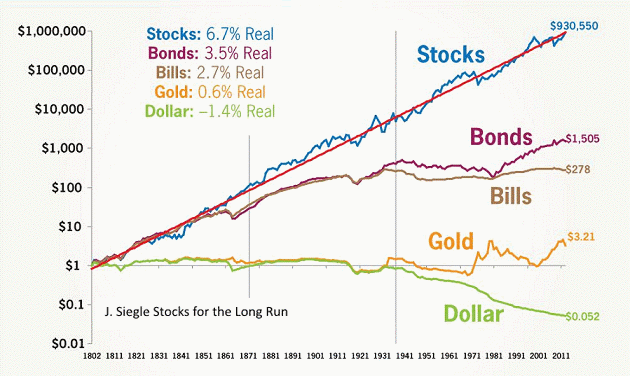
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):
Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.
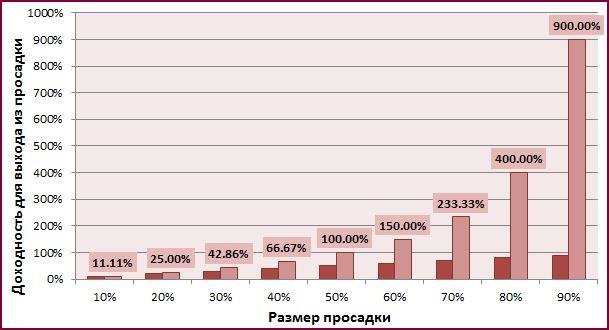
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:
Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.
В общем случае формула доходности выглядит так:
A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1
- A(0) – исходное количество денег
- А(n) – количество денег через n лет
- X – годовая доходность (в процентах)
Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то
A(n) = A(n-1) × Y = A(0) × Y^n
Задача
Актив растет на 10% в год. Какова будет его доходность через 2 года?
Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу
А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)
Обратная задача
Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):
Снова принимая нашу первоначальную доходность за условную единицу, считаем:
Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%
Задача 2
За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?
Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%
Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).
Задача 3
За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?
2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда
Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%
Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.
Задача 4
Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?
Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%
Задача 5
Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.
2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%
Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:
1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)
И средняя инфляция
Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%
P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.
Задача 6
Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?
Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.
Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.
Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).
Задача 7
Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.
Y = [(7.2 + (135-120))/120] × 100% = 18.5%
Задача 8
По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:
Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%
Источник
Средняя (среднегодовая) доходность: как рассчитать?
Средняя (среднегодовая) доходность может быть интересна в некоторых случаях, когда мы оцениваем перспективы инвестиций на длительном сроке и сравниваем среднюю доходность между собой у разных инструментов вложений, а также с другими показателями, типа уровня инфляции за год.
Итак, допустим у нас есть данные по общей доходности актива, либо известна начальная и конечная цена (стоимость, значение) чего-то. Разумеется, нужно знать временной период для вычисления средней годовой доходности.
Пример расчёта средней годовой доходности
| Пример. Вычислим среднюю годовую доходность золота за период с 2000 по 2008 год (включительно), то есть период: 9 лет. Для расчёта можно взять данные о цене за тройскую унцию (31 грамм) на какой-нибудь товарной бирже, базирующейся в одном из мировых финансовых центов. Но мы для простоты возьмём учётные цены Центробанка России на золото (рублей за 1 грамм) на последнее число декабря. |
Исходные данные:
- период: 9 лет
- начальная цена: 238,62 рублей (31 декабря 1999 года)
- конечная цена: 821,80 рублей (31 декабря 2008 года)
Воспользуемся математической формулой для вычисления средней доходности. Вот она:
Либо в таком виде (формула одна и та же, просто написана по разному):
- цена2 — конечная цена в рассматриваемом периоде
- цена1 — начальная цена в рассматриваемом периоде
- n — период в годах.
Подставим наши значения в формулу и получим:
Калькулятор накоплений
Поскольку доходность (в отличии от дохода) измеряется в процентах, умножим получившееся значение на 100% и получим среднюю годовую доходность золота за 9 лет (2000-2008г), равную 14,7% .
Формула расчёта средней доходности вытекает из формулы сложного процента. Если вы хотите углубиться в математику и узнать, как выводится вышеприведённая формула, нажмите на рисунок ниже.

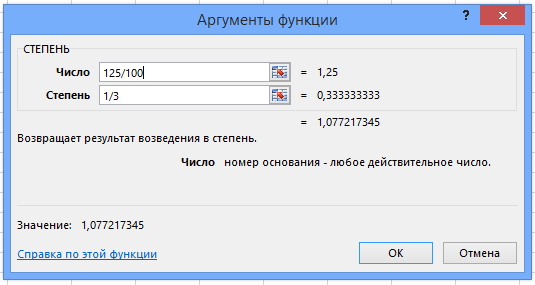
Таким образом можно вычислить среднюю годовую доходность любого инструмента. Это можно сделать на научном калькуляторе, но проще посчитать в Экселе. Для этого нам понадобится формула «СТЕПЕНЬ».
=СТЕПЕНЬ( число ; степень )
Итак, для того, чтобы быстро посчитать в Экселе вышеописанный пример, нужно ввести такую строчку:
Источник
Как считать доходность инвестиций: формулы расчета
Автор: Алексей Мартынов · Опубликовано 01.06.2015 · Обновлено 05.11.2015

Доходность (норма доходности, уровень доходности) — это степень увеличения (или уменьшения) инвестированной суммы за определенный период времени. В отличие от дохода, который выражается в номинальных величинах, то есть в рублях, долларах или евро, доходность выражается в процентах. Доход можно получать в двух видах:
- процентный доход — это проценты по депозитам, купоны по облигациям, дивиденды по акциям, арендная плата по недвижимости;
- рост стоимости купленных активов — когда цена продажи актива больше цены покупки — это акции, облигации, недвижимость, золото, серебро, нефть и другие товарные активы.
Такие активы как недвижимость, акции и облигации могут сочетать в себе два источника дохода. Расчет доходности нужен для оценки роста или падения вложений и является критерием оценки эффективности инвестиций.
Как рассчитать доходность инвестиций?
В общем виде доходность всегда рассчитывается как прибыль (или убыток), деленная на сумму вложенных средств, умноженная на 100%. Прибыль считается как сумма продажи актива — сумма покупки актива + сумма денежных выплат, полученных за период владения активом, то есть процентный доход.
Формула 1
Мы купили акцию по цене 100 рублей (сумма вложений), продали акцию по цене 120 рублей (сумма продажи), за период владения акцией получили 5 рублей дивидендов (денежные выплаты). Считаем доходность: (120-100+5)/100 = 0,25 ∗ 100% = 25%.
Формула 2
Есть вторая формула, по которой доходность считается как сумма продажи актива + сумма денежных выплат, деленная на сумму вложений, минус 1, умноженная на 100%.
Как считать доходность в процентах годовых?
В формуле расчета простой доходности не учитывается такой важный параметр, как время. 25% можно получить за месяц, а можно и за 5 лет. Как тогда корректно сравнить доходность активов, время владения которыми различается? Для этого считают доходность в процентах годовых. Доходность в процентах годовых рассчитывается для того, чтобы сравнить друг с другом эффективность активов, время владения которыми отличается. Доходность в процентах годовых — это доходность, приведенная к единому знаменателю — доходности за год.
К примеру банковский вклад дает 11% в год, а какие-то акции принесли 15% за 1,5 года владения ими, что было выгоднее? На первый взгляд акции, они ведь принесли доходность больше. Но инвестор владел ими больше на полгода, поэтому их доходность как бы растянута во времени по сравнению с депозитом. Поэтому, чтобы корректно сравнить депозит и акции, доходность акций нужно пересчитать в процентах годовых.
Для этого в формулу добавляется коэффициент 365/T, где Т — количество дней владения активом.
Мы купили акцию за 100 рублей, продали через 1,5 года за 115 рублей. 1,5 года это 1,5*365=547 дней.
(115-100)/100 ∗ 365/547 ∗ 100% = 10%. В этом случае депозит оказался немного выгоднее акций.
Как форекс, управляющие компании, брокеры и банки манипулируют годовой доходностью.
В любой рекламе доходности обращайте внимание на сноски, уточняйте какую доходность указывают в рекламе и за какой период. К примеру, в рекламе звучит доходность 48% годовых. Но она может быть получена всего лишь за один месяц. То есть компания за месяц заработала 4% и теперь с гордостью рекламирует продукт, дающий 4*12=48% годовых. Даже вы, заработав за день на бирже 1%, можете хвастаться, что заработали 365% годовых) Только доходность эта виртуальная.
 Как считать среднегодовую доходность
Как считать среднегодовую доходность
Срок владения активами может составлять несколько лет. При этом большинство активов не растет на одну и ту же величину. Такие активы как акции могут падать или расти на десятки или сотни процентов в год. Поэтому хочется знать, сколько в среднем в год росли ваши инвестиции. Как тогда вычислить среднюю годовую доходность? Среднегодовая доходность рассчитывается через извлечение корня по формуле:
Формула 1
где n — количество лет владения активом.
3√125/100 — 1 ∗ 100% = 7,72%
Формула 2
Другая формула расчета среднегодовой доходности — через возведение в степень.

Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Если известны доходности актива по годам, то среднюю годовую доходность можно вычислить перемножив годовые доходности и извлечь из произведения корень в степени равной количеству лет.
Для начала переведите доходности из процентов в числа.
Эти формулы учитывают эффект сложных процентов. Простая формула расчета доходности этого не учитывает и завышает доходность, что не совсем правильно.
Источник








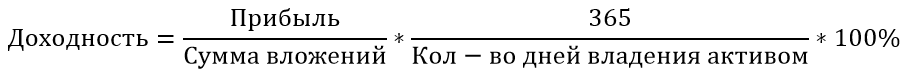
 Как считать среднегодовую доходность
Как считать среднегодовую доходность