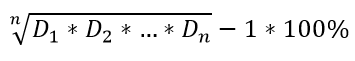- Как считать доходность инвестиций: формулы расчета
- Как рассчитать доходность инвестиций?
- Как считать доходность в процентах годовых?
- Как считать среднегодовую доходность
- Как рассчитать среднюю годовую доходность, если известны доходности по годам?
- Сложный процент. Формулы расчета сложного процента
- Формула сложного процента (расчет в годах)
- Формула сложного процента (расчет в месяцах)
- Формула сложного процента для банковских вкладов
Как считать доходность инвестиций: формулы расчета
Автор: Алексей Мартынов · Опубликовано 01.06.2015 · Обновлено 05.11.2015

Доходность (норма доходности, уровень доходности) — это степень увеличения (или уменьшения) инвестированной суммы за определенный период времени. В отличие от дохода, который выражается в номинальных величинах, то есть в рублях, долларах или евро, доходность выражается в процентах. Доход можно получать в двух видах:
- процентный доход — это проценты по депозитам, купоны по облигациям, дивиденды по акциям, арендная плата по недвижимости;
- рост стоимости купленных активов — когда цена продажи актива больше цены покупки — это акции, облигации, недвижимость, золото, серебро, нефть и другие товарные активы.
Такие активы как недвижимость, акции и облигации могут сочетать в себе два источника дохода. Расчет доходности нужен для оценки роста или падения вложений и является критерием оценки эффективности инвестиций.
Как рассчитать доходность инвестиций?
В общем виде доходность всегда рассчитывается как прибыль (или убыток), деленная на сумму вложенных средств, умноженная на 100%. Прибыль считается как сумма продажи актива — сумма покупки актива + сумма денежных выплат, полученных за период владения активом, то есть процентный доход.
Формула 1
Мы купили акцию по цене 100 рублей (сумма вложений), продали акцию по цене 120 рублей (сумма продажи), за период владения акцией получили 5 рублей дивидендов (денежные выплаты). Считаем доходность: (120-100+5)/100 = 0,25 ∗ 100% = 25%.
Формула 2
Есть вторая формула, по которой доходность считается как сумма продажи актива + сумма денежных выплат, деленная на сумму вложений, минус 1, умноженная на 100%.
Как считать доходность в процентах годовых?
В формуле расчета простой доходности не учитывается такой важный параметр, как время. 25% можно получить за месяц, а можно и за 5 лет. Как тогда корректно сравнить доходность активов, время владения которыми различается? Для этого считают доходность в процентах годовых. Доходность в процентах годовых рассчитывается для того, чтобы сравнить друг с другом эффективность активов, время владения которыми отличается. Доходность в процентах годовых — это доходность, приведенная к единому знаменателю — доходности за год.
К примеру банковский вклад дает 11% в год, а какие-то акции принесли 15% за 1,5 года владения ими, что было выгоднее? На первый взгляд акции, они ведь принесли доходность больше. Но инвестор владел ими больше на полгода, поэтому их доходность как бы растянута во времени по сравнению с депозитом. Поэтому, чтобы корректно сравнить депозит и акции, доходность акций нужно пересчитать в процентах годовых.
Для этого в формулу добавляется коэффициент 365/T, где Т — количество дней владения активом.
Мы купили акцию за 100 рублей, продали через 1,5 года за 115 рублей. 1,5 года это 1,5*365=547 дней.
(115-100)/100 ∗ 365/547 ∗ 100% = 10%. В этом случае депозит оказался немного выгоднее акций.
Как форекс, управляющие компании, брокеры и банки манипулируют годовой доходностью.
В любой рекламе доходности обращайте внимание на сноски, уточняйте какую доходность указывают в рекламе и за какой период. К примеру, в рекламе звучит доходность 48% годовых. Но она может быть получена всего лишь за один месяц. То есть компания за месяц заработала 4% и теперь с гордостью рекламирует продукт, дающий 4*12=48% годовых. Даже вы, заработав за день на бирже 1%, можете хвастаться, что заработали 365% годовых) Только доходность эта виртуальная.
 Как считать среднегодовую доходность
Как считать среднегодовую доходность
Срок владения активами может составлять несколько лет. При этом большинство активов не растет на одну и ту же величину. Такие активы как акции могут падать или расти на десятки или сотни процентов в год. Поэтому хочется знать, сколько в среднем в год росли ваши инвестиции. Как тогда вычислить среднюю годовую доходность? Среднегодовая доходность рассчитывается через извлечение корня по формуле:
Формула 1
где n — количество лет владения активом.
3√125/100 — 1 ∗ 100% = 7,72%
Формула 2
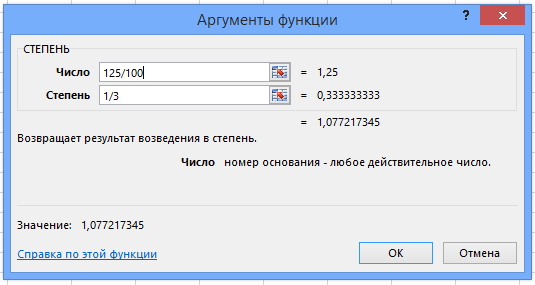
Другая формула расчета среднегодовой доходности — через возведение в степень.

Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Если известны доходности актива по годам, то среднюю годовую доходность можно вычислить перемножив годовые доходности и извлечь из произведения корень в степени равной количеству лет.
Для начала переведите доходности из процентов в числа.
Эти формулы учитывают эффект сложных процентов. Простая формула расчета доходности этого не учитывает и завышает доходность, что не совсем правильно.
Источник
Сложный процент. Формулы расчета сложного процента
Люди во все времена думали о своем завтрашнем дне. Они старались и стараются обезопасить от финансовых невзгод и себя, и своих детей и внуков, строя хотя бы небольшой островок уверенности в будущем. Начиная строить его уже сейчас с помощью небольших банковских вкладов, можно обеспечить себе в дальнейшем стабильность и независимость.
Основным принципом банковских операций является то, что денежные средства способны увеличиваться лишь тогда, когда находятся в постоянном обороте. Чтобы клиентам уверенно ориентироваться в сфере финансовых услуг и уметь правильно подбирать условия, выгодные им в определенный промежуток времени, необходимо знать ряд простых правил. В данной статье речь пойдет о долгосрочных вложениях, которые позволяют за определенное количество лет из относительно небольшой суммы начального капитала получить существенную прибыль или использовать вклад дальше, снимая начисления для повседневных нужд.
Для правильного расчета прибыли необходимо выполнить несложные арифметические действия на основе нижеизложенных формул.
Формула сложного процента (расчет в годах)
Например, вы решили положить 100000,00 руб. под 11% годовых, чтобы через 10 лет воспользоваться сбережениями, которые значительно выросли в результате капитализации. Для расчета итоговой суммы следует применить методику расчета сложного процента.
Для расчета сложного процента применяем простую формулу:
- S – общая сумма («тело» вклада + проценты), причитающаяся к возврату вкладчику по истечении срока действия вклада;
- Р – первоначальная величина вклада;
- n — общее количество операций по капитализации процентов за весь срок привлечения денежных средств (в данном случае оно соответствует количеству лет);
- I – годовая процентная ставка.
Подставив значения в эту формулу, мы видим, что:
через 5 лет сумма будет равняться 
а через 10 лет она составит 
Если бы мы рассчитывали капитализацию процентов по вкладу за короткий период, то сложный процент было бы удобнее рассчитывать по формуле
- К – количество дней в текущем году,
- J – количество дней в периоде, по итогам которого банком производится капитализация начисленных процентов (остальные обозначения – как и в предыдущей формуле).
Но тем, кому удобнее ежемесячно снимать проценты по вкладу, лучше ознакомиться с понятием «капитализация вклада», подразумевающим начисление простых процентов.
На графике показано как вырастет капитал при капитализации процентов по вкладу, если вложить 100000,00 руб. на 10 лет под 10%, 15% и 20%
Формула сложного процента (расчет в месяцах)
Существует и другой, более выгодный для клиента метод начисления и прибавления процентной ставки – ежемесячный. Для этого применяется следующая формула:
где n также соответствует количеству операций по капитализации, но уже выражается в месяцах. Процентный показатель здесь дополнительно делится на 12 потому что в году 12 месяцев, а у нас появляется необходимость в расчете месячную процентную ставку.
Если бы данная формула использовалась для поквартального начисления вклада, то годовой процент делился бы на 4, а показатель n был бы равен количеству кварталов, а если бы процент начислялся по полугодиям, то процентная ставка делилась бы 2, а обозначение n соответствовало количеству полугодий.
Итак, если бы нами был сделан вклад в сумме 100000,00 руб. с ежемесячной капитализацией процентов, то:
через 5 лет (60 месяцев) сумма вклада выросла бы до 172891,57 руб., что примерно на 10000 руб. больше, чем в случае с ежегодной капитализацией вклада; 
а через 10 лет (120 месяцев) «наращенная» сумма составила бы 298914,96 руб., что уже на целых 15000 руб. превосходит показатель, рассчитанный по формуле сложного процента, предусматривающей расчет в годах.

Это означает, что доходность при ежемесячном начислении процентов оказывается больше, чем при начислении один раз в год. И если прибыль не снимать, то сложный процент работает на пользу вкладчика.
График, показывающий разницу роста капитала при расчете в годах и при ежемесячной капитализации процентов
Формула сложного процента для банковских вкладов
Вышеописанные формулы сложного процента – это, скорее всего, наглядные примеры для клиентов, чтобы они могли понять порядок начисления сложных процентов. Эти расчеты несколько проще, чем формула, применяемая банками к реальным банковским вкладам.
Здесь используется такая единица, как коэффициент процентной ставки для вклада (p). Его рассчитывают так:
- i – процентная ставка по вкладу (вычисляется путем деления размера годовых процентов на 100, например, если годовая ставка 11%, то
- J – период по итогам которого происходит начисление процентов, выраженный в днях;
- K – количество дней в году (365 или 366).
Эти данные дают возможность рассчитать процентную ставку для разных периодов вклада.
Сложный процент («наращенная» сумма) для банковских вкладов рассчитывается по следующей формуле:
На ее основе и взяв в качестве примера те же данные, мы рассчитаем сложный процент по банковскому методу.
Для начала определяем коэффициент процентной ставки для вклада:
Теперь подставляем данные в основную формулу:


*Приведенные в примерах расчеты являются приблизительными, поскольку в них не учтены високосные года и разное количество дней в месяце.
Если сравнивать суммы из этих двух примеров с предыдущими, то они несколько меньше, но все же выгода от капитализации процентов очевидна. Поэтому, если вы твердо решили положить деньги в банк на длительный срок, то предварительный подсчет прибыли лучше делать с помощью «банковской» формулы – это поможет вам избежать разочарований.
Источник



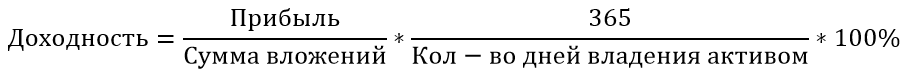
 Как считать среднегодовую доходность
Как считать среднегодовую доходность