Изменение рыночных ставок доходности

Что происходит с доходностями облигаций, когда рынки растут или падают

Что такое рыночная доходность облигации, что именно она показывает и стоит ли паниковать, если бумаги в вашем портфеле падают вместе с рынком.

Объясняем с помощью инфографики, как меняется доходность ваших облигаций в зависимости от поведения рыночных ставок и почему изменение текущей стоимости портфеля в период краткосрочных шоков не играет решающей роли для инвестора в долговые инструменты.

© При использовании материалов сайта и цитировании — ссылка с URL-адресом обязательна

Почему доходность облигации растет или падает?

Облигации и депозиты — это инструменты, в основе которых лежит рыночная процентная ставка.

Для российского рынка таким ключевым индикатором денежно-кредитной политики является ключевая ставка ЦБ. Это тот процент, под который регулятор финансирует банки, поэтому ключевая ставка напрямую влияет на ставки по кредитам и депозитам всей банковской системы, или, проще говоря, она отражает стоимость денег в экономике.

Если рыночная процентная ставка меняется, то изменяются ставки и по всем инструментам, которые к ней привязаны.

Однако в ситуации с облигациями и депозитами этот механизм работает по-разному.

К примеру, вы открыли вклад в банке сроком на 5 лет под 6% годовых. Но через год ставки на рынке выросли: теперь банк готов привлекать новые вклады на 4 года под 7% годовых. Но это не значит, что он готов будет дополнительно доплачивать 1% годовых по вашему вкладу. Таковы условия депозитного договора: ставка в нем фиксируется на весь период действия вклада.

То же самое правило действует и в обратной ситуации. Если вы открыли вклад на 5 лет по ставке 6% годовых, а через год ставки по 4-летнему новому вкладу стали ниже и составили 5% годовых, банк продолжит вам платить по вкладу 6% годовых, как зафиксировано в договоре.

А как у облигаций?

В отличие от депозитов, облигации — это рыночный инструмент. Это означает, что именно рынок (инвесторы и эмитенты) определяет ставку (доходность к погашению) по всем облигациям с любым сроком погашения в любой момент времени.

Покупая облигацию, вы фиксируете для себя доходность к погашению, с которой торгуется эта бумага в данный момент. По сути, доходность к погашению складывается из количества выплаченных купонов и ставки купона, которые определены изначально. То есть доходность к погашению — это и есть та самая эффективная рыночная ставка, купон — фиксированный процент, а количество купонов — количество выплат процентов по вкладу, который вы могли бы открыть в банке.

Разберем на примере с помощью инфографики.

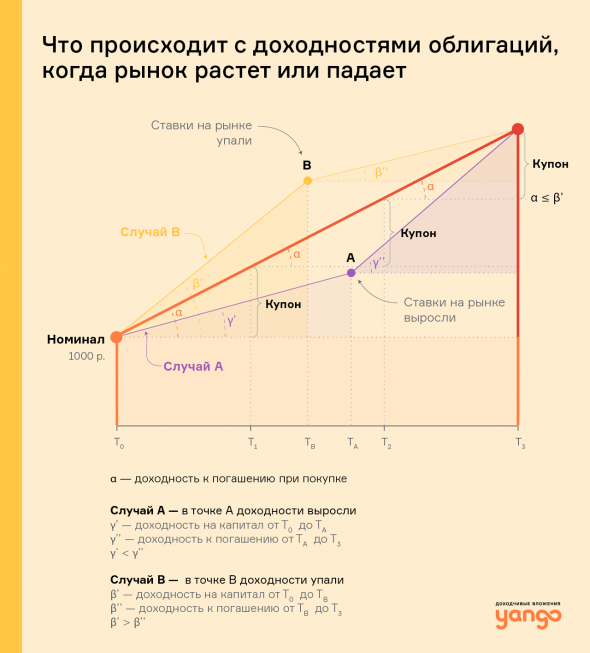
Допустим, вы приобрели облигацию в конце 2018-го — начале 2019 года (Т_о) с доходностью 10.5% годовых. Бумага погашается через 3 года, имеет 12 купонов и ставку купона 10% годовых.

Прошло чуть больше года, и в момент времени Т_в (случай В) ставки на рынке снизились (до 7% годовых — по облигациям с погашением менее чем через 2 года). Это означает, что теперь инвесторы готовы покупать облигации эмитентов того же кредитного качества, что и облигация в вашем портфеле, но уже с меньшей доходностью к погашению. За прошедший период ваша доходность на капитал по купленной облигации будет выше 10.5% годовых (угол α на рисунке) и составит примерно 16% годовых (угол β’), а за оставшееся до погашения время вы заработаете 7% годовых (угол β’’) — меньше, чем доходность к погашению (α), с которой вы приобрели облигацию изначально. Однако за 3 года вы все равно получите свои 10.5% годовых — то есть именно ту доходность к погашению, которую зафиксировали изначально при покупке бумаги.

Теперь рассмотрим обратную рыночную ситуацию. В момент времени Т_А ставки на рынке выросли (случай А на рисунке), например, до 12% годовых по инструментам с погашением менее чем через 2 года. За время, прошедшее с момента покупки облигации, ваша доходность на капитал по купленной облигации (угол γ’) составит 6% годовых — это меньше, чем доходность к погашению (угол α), с которой вы приобрели облигацию. Но с даты Т_А и до даты погашения облигации вы получите доходность к погашению (она равна будущей доходности на капитал — угол γ’’) в размере 12% годовых. Это больше, чем доходность к погашению (угол α), с которой вы изначально приобрели облигацию.

Но в любом случае за время, прошедшее с Т_о до Т₃ (даты погашения облигации) вы получите доходность, с которой изначально приобретали бумагу — ту самую доходность к погашению (угол α).

Когда ставки на рынке изменяются в ту или другую сторону (как мы писали выше), доходность к погашению (от текущей даты до даты погашения) тоже изменяется. Так как купон по облигациям фиксированный и определяется в момент первичного размещения бумаг, то изменение доходности к погашению происходит за счет изменения цены облигации (в процентах /рублях). В случае В она растет, в случае А — падает.

Проще говоря: если ставки упали, вы платите больше, чтобы получить меньшую доходность к погашению по сравнению с доходностью к погашению при первичном размещении. Ставки выросли — вы покупаете облигацию с большей доходностью к погашению, чем доходность к погашению при первичном размещении. Большая доходность при покупке получается за счет разницы в цене (цена погашения — цена покупки) купонного дохода. Подробно о том, как связана цена с доходностью к погашению, мы рассказывали тут.

Почему изменение текущей стоимости портфеля — не повод для паники?

Если бумаги в вашем портфеле снижаются или растут вместе с рынком, это нормальная ситуация.

Заходя в приложение Yango в любой момент времени, вы видите рыночную доходность к погашению по облигациям. Это та доходность, которую вы получаете начиная от текущего момента и до даты погашения. Она не показывает ваши убытки или прибыли, а всего лишь отражает рыночную ситуацию.

Если текущая доходность ниже той доходности, с которой вы приобретали облигации, то это означает, что вы находитесь в точке В (то есть ставки на рынке снизились, а цены выросли).

И наоборот: когда текущая доходность выше той, что вы зафиксировали при покупке облигации (что мы и наблюдаем на рынке сейчас), то вы находитесь в точке А, а значит, рыночные ставки растут, а цены падают.

Пройдет время, волатильность на рынке снизится, доходности снова начнут снижаться, а цены восстановятся.

Что делать инвестору?

Обычно рыночная коррекция, которая сопровождается ростом доходностей, — отличная возможность сделать выгодные покупки, вложившись в бумаги хорошего качества по привлекательным ставкам. Поэтому, если у вас есть свободный остаток на счете, как раз самое время инвестировать его в рынок инструментов с фиксированным доходом.

Полную версию инфографики можно скачать тут.

Источник

Что происходит с доходностями облигаций, когда рынки растут или падают

Нашел на странице фейсбука у Игоря Лаухина

Облигации и депозиты — это инструменты, в основе которых лежит рыночная процентная ставка.

Для российского рынка таким ключевым индикатором денежно-кредитной политики является ключевая ставка ЦБ. Это тот процент, под который регулятор финансирует банки, поэтому ключевая ставка напрямую влияет на ставки по кредитам и депозитам всей банковской системы, или, проще говоря, она отражает стоимость денег в экономике.

Если рыночная процентная ставка меняется, то изменяются ставки и по всем инструментам, которые к ней привязаны.

Однако в ситуации с облигациями и депозитами этот механизм работает по-разному.

К примеру, вы открыли вклад в банке сроком на 5 лет под 6% годовых. Но через год ставки на рынке выросли: теперь банк готов привлекать новые вклады на 4 года под 7% годовых. Но это не значит, что он готов будет дополнительно доплачивать 1% годовых по вашему вкладу. Таковы условия депозитного договора: ставка в нем фиксируется на весь период действия вклада.

То же самое правило действует и в обратной ситуации. Если вы открыли вклад на 5 лет по ставке 6% годовых, а через год ставки по 4-летнему новому вкладу стали ниже и составили 5% годовых, банк продолжит вам платить по вкладу 6% годовых, как зафиксировано в договоре.

А как у облигаций?

В отличие от депозитов, облигации — это рыночный инструмент. Это означает, что именно рынок (инвесторы и эмитенты) определяет ставку (доходность к погашению) по всем облигациям с любым сроком погашения в любой момент времени.

Покупая облигацию, вы фиксируете для себя доходность к погашению, с которой торгуется эта бумага в данный момент. По сути, доходность к погашению складывается из количества выплаченных купонов и ставки купона, которые определены изначально. То есть доходность к погашению — это и есть та самая эффективная рыночная ставка, купон — фиксированный процент, а количество купонов — количество выплат процентов по вкладу, который вы могли бы открыть в банке.

Разберем на примере с помощью инфографики.

Допустим, вы приобрели облигацию в конце 2018-го — начале 2019 года (То) с доходностью 10.5% годовых. Бумага погашается через 3 года, имеет 12 купонов и ставку купона 10% годовых.

Прошло чуть больше года, и в момент времени Тв (случай В) ставки на рынке снизились (до 7% годовых — по облигациям с погашением менее чем через 2 года). Это означает, что теперь инвесторы готовы покупать облигации эмитентов того же кредитного качества, что и облигация в вашем портфеле, но уже с меньшей доходностью к погашению. За прошедший период ваша доходность на капитал по купленной облигации будет выше 10.5% годовых (угол α на рисунке) и составит примерно 16% годовых (угол β’), а за оставшееся до погашения время вы заработаете 7% годовых (угол β’’) — меньше, чем доходность к погашению (α), с которой вы приобрели облигацию изначально. Однако за 3 года вы все равно получите свои 10.5% годовых — то есть именно ту доходность к погашению, которую зафиксировали изначально при покупке бумаги.

Теперь рассмотрим обратную рыночную ситуацию. В момент времени ТА ставки на рынке выросли (случай А на рисунке), например, до 12% годовых по инструментам с погашением менее чем через 2 года. За время, прошедшее с момента покупки облигации, ваша доходность на капитал по купленной облигации (угол γ’) составит 6% годовых — это меньше, чем доходность к погашению (угол α), с которой вы приобрели облигацию. Но с даты ТА и до даты погашения облигации вы получите доходность к погашению (она равна будущей доходности на капитал — угол γ’’) в размере 12% годовых. Это больше, чем доходность к погашению (угол α), с которой вы изначально приобрели облигацию.

Но в любом случае за время, прошедшее с То до Т3 (даты погашения облигации) вы получите доходность, с которой изначально приобретали бумагу — ту самую доходность к погашению (угол α).

Когда ставки на рынке изменяются в ту или другую сторону (как мы писали выше), доходность к погашению (от текущей даты до даты погашения) тоже изменяется. Так как купон по облигациям фиксированный и определяется в момент первичного размещения бумаг, то изменение доходности к погашению происходит за счет изменения цены облигации (в процентах /рублях). В случае В она растет, в случае А — падает.

Проще говоря: если ставки упали, вы платите больше, чтобы получить меньшую доходность к погашению по сравнению с доходностью к погашению при первичном размещении. Ставки выросли — вы покупаете облигацию с большей доходностью к погашению, чем доходность к погашению при первичном размещении. Большая доходность при покупке получается за счет разницы в цене (цена погашения — цена покупки) купонного дохода.

Почему изменение текущей стоимости портфеля — не повод для паники?

Если бумаги в вашем портфеле снижаются или растут вместе с рынком, это нормальная ситуация.
Это та доходность, которую вы получаете начиная от текущего момента и до даты погашения. Она не показывает ваши убытки или прибыли, а всего лишь отражает рыночную ситуацию.

Если текущая доходность ниже той доходности, с которой вы приобретали облигации, то это означает, что вы находитесь в точке В (то есть ставки на рынке снизились, а цены выросли).

И наоборот: когда текущая доходность выше той, что вы зафиксировали при покупке облигации (что мы и наблюдаем на рынке сейчас), то вы находитесь в точке А, а значит, рыночные ставки растут, а цены падают.

Пройдет время, волатильность на рынке снизится, доходности снова начнут снижаться, а цены восстановятся.

Источник

Расчет рыночной доходности

Формула расчета рыночной доходности

Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.

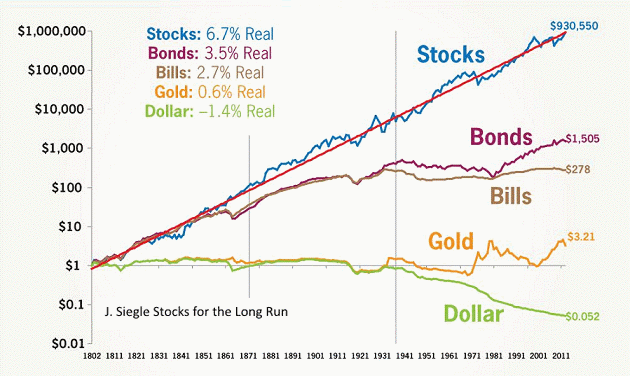
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):

Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.

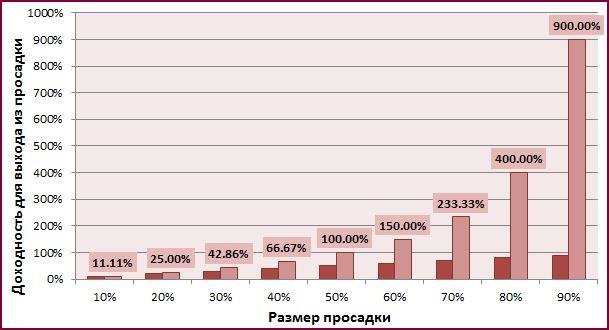
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:

Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.

В общем случае формула доходности выглядит так:

A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1

1. A(0) – исходное количество денег
2. А(n) – количество денег через n лет
3. X – годовая доходность (в процентах)

Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то

A(n) = A(n-1) × Y = A(0) × Y^n

Задача

Актив растет на 10% в год. Какова будет его доходность через 2 года?

Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу

А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)

Обратная задача

Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):

Снова принимая нашу первоначальную доходность за условную единицу, считаем:

Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%

Задача 2

За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?

Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%

Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).

Задача 3

За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?

2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда

Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%

Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.

Задача 4

Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?

Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%

Задача 5

Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.

2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%

Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:

1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)

И средняя инфляция

Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%

P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.

Задача 6

Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?

Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.

Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.

Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).

Задача 7

Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.

Y = [(7.2 + (135-120))/120] × 100% = 18.5%

Задача 8

По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:

Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%

Источник