Изменение инвестиций во времени

Финансовая статистика: конспект лекций.

Изменение во времени инвестиций в основной капитал.

На основании экстраполяции прогнозное значение дальнейшего роста уровня инвестиций в основной капитал можно рассчитать как:

Средний темп роста, согласно примеру, находится как корень четвертой степени из произведения цепных коэффициентов роста:

Следовательно, прогнозируемый уровень у_n+1 = 1130,2 + 116 % = 2441,2 млрд руб.

Главной задачей экономического анализа инвестиций является определение их эффективности, т. е. экономической категории, характеризующей соотношение осуществленных в процессе хозяйственной деятельности затрат ресурсов и полученного за этот счет результата.

Особенно широко используются статистические методы при изучении финансовых инвестиций. В основе изучения финансовых инвестиций лежит построение уравнения эквивалентности, так называемого баланса финансовой операции. Понятие финансовой эквивалентности является основой в количественном финансовом анализе. Содержание данного анализа заключается в приведении денежных потоков, связанных с инвестицией, к единому моменту времени – в основном моменту инвестирования (или завершения процесса получения доходов по инвестиции) – и приравнивании суммы отрицательных (взятых по абсолютной величине) элементов денежного потока к сумме положительных элементов.

Эффективность финансовых инвестиций характеризуется их доходностью. Инвестиции в акции – это разновидность финансовых инвестиций, т. е. инвестирование денежных средств в финансовые активы с целью получения дохода. Доходными являются вложения в акции, обеспечивающие доход выше среднерыночного. Доходность ценных бумаг за определенный период исчисляется по формуле:

Где Б_н – благосостояние инвестора на начало периода;

Б_к – благосостояние инвестора на конец периода.

В конкретном случае, т. е. в формуле, под благосостоянием на начало периода понимается покупная цена ценных бумаг в этот момент, а на конец периода – рыночная цена ценных бумаг в конце периода с учетом всех выплат доходов по ним за указанный период.

Предположим, акции какой-либо компании продавались по 1970 руб. в начале года и по 2230 руб. в конце года и, к тому же, в течение года выплачивались дивиденды в сумме 570 руб. Следовательно, доходность акций компании за год составит: (2230 + + 570-1970) / 1970 = 0,42 или 42 %. Данная формула используется для расчета доходности за конкретный период как в случае приобретения ценных бумаг в начале периода (при этом благосостояние на начало периода принимается равным цене приобретения ценных бумаг), так и в случае, если ценные бумаги к началу периода уже находились в собственности инвестора (при этом благосостояние на начало периода принимается равным действующим в указанный момент рыночным ценам на данные ценные бумаги).

Доходность ценной бумаги за конкретный период может быть представлена в виде суммы двух величин, одна из которых зависит от изменения рыночной цены (курса) данной ценной бумаги за этот период, а другая – от выплаты доходов по этой бумаге. Следовательно, формула принимает следующий вид:

Где РЦБн – рыночная цена ценной бумаги в начале периода;

РЦБк – рыночная цена ценной бумаги в конце периода;

ВД – выплаты доходов по ценной бумаге за период.

Соответственно доходность акций по этой формуле рассчитывается следующим образом:

Доходность = (2230/1970 + 570/1970) – 1 = 0,42.

Так как на фондовом рынке продается много различных ценных бумаг, имеющих разную доходность, то средняя рыночная доходность всех циркулирующих на рынке акций (r_м) определяется по формуле:

Где r_i – доходность i-й акции (в долях единицы);

х_i – относительная рыночная стоимость i-й акции, равная совокупной рыночной стоимости всех выпущенных акций этого наименования, деленной на сумму совокупных рыночных стоимостей всех присутствующих на рынке акций;

N– количество наименований всех имеющихся на рынке акций.

В основном в качестве r_i применяется отношение рыночной стоимости данной ценной бумаги в конце анализируемого периода к ее рыночной стоимости в начале этого периода, а используемые показатели называются рыночными индексами. В мировой практике применяется ряд таких показателей, несколько отличающихся алгоритмами расчета (например, Stаndаrt аmр; Рооr’s Stоск Рriсе Indех, представляющий собой средневзвешенную величину курсов акций 500 крупнейших корпораций США). В России по подобной методике рассчитывается индекс «РТС-Интерфакс», обобщающий данные об изменении рыночной стоимости 100 обращающихся на российском рынке наиболее ликвидных акций, а также известен индекс АК аmр; М и некоторые другие.

Для эффективной работы на фондовом рынке необходимо знать, как доходность конкретного наименования акций (или портфеля акций конкретного инвестора) связана со средней рыночной доходностью всей совокупности акций, т. е. с рыночным индексом. Для этого применяются статистические модели.

Простейшая линейная модель предусматривает существование следующей связи:

Источник

Различные аспекты влияния фактора времени

Одно из основных положений теории оценки эффективности инвестиционных проектов — необходимость учета фактора времени. Проявления этого фактора:

• динамичность технико-экономических показателей предприятия. Особенно важно учитывать изменения во времени объемов и структуры производимой продукции, норм расхода сырья, численности персонала, длительности производственного цикла, норм запасов и т. п. в период освоения вводимых мощностей, а также в проектах, предусматривающих последовательное техническое перевооружение производства в период реализации проекта или разработку сырьевых месторождений. Динамичность показателей учитывается при формировании исходной информации по шагам расчетного периода;
• сезонность производства или реализации продукции, проявляющаяся в сезонных колебаниях объемов поставки сырья, производства продукции или спроса на нее, а также запасов и дебиторской задолженности. Сезонные колебания особенно существенны в начальный период функционирования введенных производств. Их целесообразно учитывать прежде всего путем надлежащей разбивки расчетного периода на шаги. При существенных сезонных колебаниях показатели проекта зависят от того, в каком именно месяце года начнется производство продукции. Начало расчетного периода целесообразно установить в виде конкретной календарной даты;
• физический износ основных средств, обусловливающий общие тенденции к снижению их производительности и росту затрат на их содержание, эксплуатацию и ремонт на протяжении расчетного периода. Физический износ должен учитываться в исходной информации при формировании производственной программы, операционных издержек (в том числе расходов на периодически проводимый капитальный ремонт) и установлении сроков замены основного технологического оборудования. Рациональные сроки службы основных средств могут определяться на основе расчетов эффективности соответствующих вариантов проекта и в общем случае не обязательно будут совпадать с амортизационными сроками;
• изменение во времени цен на производимую продукцию и потребляемые ресурсы. Учитывается непосредственно при формировании исходной информации для расчетов эффективности;
• изменение во времени параметров внешней среды (цен, ставок, налогов, пошлин, акцизов, размеров минимальной месячной оплаты труда, налогового и иного законодательства и т. п.). Учитывается непосредственно при формировании исходной информации для расчетов эффективности;
• разрывы по времени (лаги) между производством и реализацией продукции и между оплатой и потреблением ресурсов;
• разновременность затрат, результатов и эффектов, т. е. осуществление их в течение всего периода реализации проекта, а не в какой-то один фиксированный момент времени.
  Этот аспект фактора времени учитывается в расчетах путем дисконтированияденежных потоков.

Необходимость использования сложных процентов

При принятии решения об инвестировании денег необходимо учитывать различные факторы (инфляция, риск и возможность альтернативного использования денег). Таким образом, одна и та же денежная сумма имеет различную ценность во времени по отношению к текущему моменту.

Методика начисления сложных процентов используется при необходимости решить вопрос о размере денежной суммы, которая окажется на счете в банке через t лет, если первоначальный вклад составил Р денежных единиц при ставке процента, равной г, для того чтобы найти будущую величину вклада. F(t) = P*(1+r)t,
где F(t) — будущая ценность денег в период времени t;
Р — текущая ценность денег (первоначальная ценность);
r — ставка процента;
t — продолжительность временного периода.
Более актуальным является обратное действие — определить, какую сумму в размере Р денежных единиц необходимо положить на счет сегодня, чтобы через f лет с учетом сложных процентов ее величина составила F(t) единиц:

Такое действие (сведение будущих денежных сумм к насто­ящему моменту времени) называется дисконтированием.
Множители (1 t г)’ и 1/(1 + г)’ в предыдущих формулах называются соответственно коэффициентами начисления сложных процентов и дисконтирования. Разработаны специальные таблицы, позволяющие находить значения этих коэффициентов при известной процентной ставке и продолжительности временного периода.
Если коэффициент дисконтирования года f при ставке процента, равной г, обозначить через d(t, r), то формула дисконтирования будет выглядеть так:

Пусть по некоторому проекту поток денежных средств по периодам (годам) будет иметь вид, представленный во второй колонке табл. 1, Необходимо вычислить общую суммарную стоимость потока за весь период, если известна процентная ставка, равная r.

Таблица 1. Расчет попериодных значений денежного потока

Периоды (годы)

Денежный поток

Коэффициент дисконтирования

Дисконтированный денежный поток

Источник

Время в инвестировании

Время — это архимедов рычаг в инвестировании. Чарльз Д. Эллис

Время – это один из основных факторов успешного вложения средств. Многие наверняка слышали о магии «сложного процента», когда процент начисляется на возрастающую сумму, что с годами приводит к экспоненциальному росту дохода. Исследования показывают, что фактор времени при правильном распределении активов значит несравненно больше, чем просто удачный момент входа в рынок.

Почему так? Хороший портфель включает множество инструментов и часть из них в момент покупки будут недостаточно дешевы. Но именно время даст возможность вырасти портфелю целиком, раскрыв потенциал всех его компонентов. Статья ниже призвана четко ответить на вопрос, как можно накопить капитал на фондовом рынке.

Римский педагог и оратор Квинтилиан говорил «пока мы размышляем, когда нам начать, часто бывает уже слишком поздно действовать». Рассматривая эту фразу в контексте финансового сектора, важно провести некую границу, чтобы не попасть в логическую ловушку. В чем она состоит?

При всей важности времени первостепенным для инвестора является вопрос выбора своей стратегии, тогда как его активы должны быть надежно защищены от неторговых рисков. Ошибка в этом компоненте может привести как к вложениям в финансовые пирамиды с обещанием высокого дохода, так и излишне консервативные инструменты, в результате чего результат оказывается совсем не таким, на который инвестор рассчитывал.

Однако когда видна историческая доходность рыночных инструментов и есть понимание того, как правильно инвестировать, то дальнейшие ожидания (вот начну больше зарабатывать, вырастет ребенок, упадет рынок и пр.) с копанием во второстепенных подробностях лишь все больше затрудняют задачу добиться своих финансовых целей. И уже в этой ситуации ответ на вопрос «когда начинать инвестировать» очень конкретен: как можно раньше .

Дело за тактикой – подбором конкретных фондов под выбранную стратегию с учетом склонности инвестора к риску, его возраста и пр. При этом идеальной рыночной ситуации и особенно идеального инвестиционного портфеля, непрерывно растущего в любых обстоятельствах, попросту не существует.

Влияние времени на инвестирование

Большинство примеров по инвестициям со сложным процентом, что я видел в блогах, обычно оперируют или очень большими сроками, или завышенной доходностью, что позволяет показать впечатляющую, загнутую вверх кривую. Ниже я попробую привести приближенный к практике пример, опираясь на проверенные более чем сотней лет рыночные данные.

Допустим, инвестор в возрасте 40 лет, получающий стабильную заработную плату в размере 2 тыс. долларов (на момент статьи это около 115 000 рублей), желает через 15 лет отойти от активной трудовой деятельности и иметь ежемесячный пассивный доход от вложений в размере 1 тысячи долларов (половина текущей оплаты труда).

Для этого нужно за отведенные 15 лет накопить достаточно большую сумму, но инвестиционный портфель не должен быть слишком агрессивным и рискованным. Его задача — в сохранении и приумножении средств для последующего обеспечения своего владельца пассивным доходом.

Примем, что ежемесячная рента рассчитывается из 5% от капитала в год — в нее может входить купонный или дивидендный доход, а также выплаты процентов по фондам недвижимости. Кроме того, это может быть и рост котировок, в первую очередь акций.

С таким допущением нашему инвестору необходимо накопить как минимум 240 тысяч долларов. Для этого в течение 15 лет нужно ежемесячно вкладывать 700 долларов под 8% годовых. При заработной плате в 2 тысячи долларов вложение 700 $ (чуть больше трети от текущего ежемесячного дохода) заметно для бюджета, но все же находится в рамках совмещения с ним.

Внимательные читатели заметят еще одно допущение: предполагается стабильное получение зарплаты в 2 000 $ или рублевом эквиваленте этой суммы. Но для получающих деньги в рублях после декабря 2014 ситуация резко изменилась — вносить те же 700 долларов стало бы гораздо труднее. Тем не менее ввиду нестабильности курса рубля, его короткой биржевой истории и заметной инфляции я предпочитаю вкладывать и проводить расчеты в долларах.

Откуда берутся 8% годовых? Из средней доходности фондового рынка США за всю его историю, которая примерно равна 10% в год. Однако известно, что на капитал влияет инфляция — для доллара с начала века она равна около 2%. Разница, равная 8% и есть используемая в расчете доходность.

Разумеется, нет твердой гарантии сохранения исторического роста американского рынка с той же скоростью, что и ранее — как и нет гарантии сохранения инфляции на текущем уровне (в 70-е годы она пару лет достигала двузначных чисел). Но имеем то, что имеем — для компенсации этих моментов (а также различного рода неизбежных комиссий) я заложил пониженную ренту в размере 5, а не 8% годовых. Хотя и эти числа весьма оптимистичны.

На графике ниже, учитывающим реинвестирование дивидендов фондового рынка США, за вычетом инфляции получается немного меньше 7% чистой доходности (так как инфляция в США за последние 100 лет была в среднем несколько больше, чем с 2000 года). Кроме того, хорошо видно, что доллар с 1930-х годов по 2011 обесценился на 95%:

Теперь предположим, что под влиянием непредвиденных обстоятельств инвестор отложил свои планы по вложению средств и вернулся к этому вопросу только через 3 года. Задача осталась прежней — тысяча долларов ежемесячного пассивного дохода.

Но чтобы получить необходимые для этого 240 тысяч долларов через 12 лет (а не 15, как ранее) инвестору требуется вкладывать уже не 700, а 1000 $ в месяц. За три «потерянных» года стоимость его будущей цели возросла на 300 долларов. Кроме того, сократив время, мы увеличиваем разброс результатов. Но сохранив условия выше, ежемесячные инвестиции нашего инвестора будут составлять уже не треть, а половину текущих доходов! А относительно прежнего ежемесячного вклада «добавка» выросла более, чем на 40%!

Если же инвестор будет, как и планировалось раньше, вкладывать по 700 долларов ежемесячно, его капитал через 12 лет составит 169 тыс. долларов, а ежемесячный пассивный доход — 704 $. В итоге результатом трех лет бездействия станет недополученный капитал в размере 71 тыс. долларов и уменьшение ежемесячных пассивных доходов на 296 $.

Для более крупных целей (например, при зарплате в 6 000 долларов и желаемом пассивном доходе в 3 000 $ в месяц) разница при промедлении в три года на тех же сроках получится еще более впечатляющей — ежемесячные инвестиции придется увеличить примерно с 2 100 до 3 100, т.е на 1 000 долларов.

Таким образом, чем раньше инвестор начнет вкладывать свои средства, тем большую сумму он сможет накопить к желаемому сроку, и тем дешевле будет для него выполнение намеченных планов. Ниже в таблице приведены примеры ежемесячной суммы вложений для получения 240 тысяч долларов под 8% годовых через разные сроки.

Ежемесячная сумма инвестиций, долларов	Продолжительность накопления, лет	Общая сумма вложений за время накопления, долларов
165	30	59 400
255	25	76 500
410	20	98 400
700	15	126 000
1310	10	157 200
3250	5	195 000
Общий накопленный капитал		≈ 240 тыс. долларов

Как видно, расчеты на разные сроки инвестирования подтверждают тезис о преимуществе ранних вложений по сравнению с более поздними, причем эта выгода проявляется и в ежемесячных отчислениях, и в общей сумме инвестиций. Срок 5 лет, впрочем, указан довольно условно — получение рыночной доходности хорошо работает именно на длинных интервалах от 10 лет.

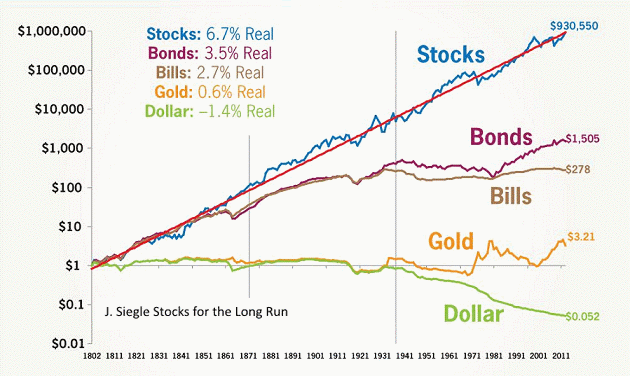
Почему? Вернемся к графику выше. Стандартное отклонение доходности на всем промежутке времени составило 18% для акций, 9% для облигаций и 6% для векселей. Для инвестора с горизонтом в 1 год акции таким образом значительно рискованней (в 2-3 раза), чем фиксированный доход.

Для десятилетнего промежутка картина не сильно отличается. Средняя доходность за лучшее десятилетие между 1802 и 1997 годами – 17% годовых, а средняя за худшее десятилетие – минус 4%. Т.е. разница в 21%. У облигаций и векселей разница в доходности соответственно 18% и 17%. Весьма близко.

Однако время уменьшает разрыв и разница между доходностью за двадцать лет практически одинакова для всех видов активов: 12 %. А вот за 30 лет ситуация и вовсе выглядит нелогично, так как у акций изменчивость доходности получается даже меньше, чем у облигаций (лучшие и худшие 30-ти летние периоды в 20 веке давали доходность акций США 15% и 8% годовых, т.е. разница 7%).

Что это значит? Что продержав акции значительное время, мы можем получить высокую доходность с риском, равным или даже чуть меньшим, чем будучи вкладчиком облигаций!

Источник