- IRR: формула расчета, экономический смысл
- Определение и формула внутренней нормы доходности IRR
- Экономический смысл IRR
- Расчет IRR в Excel пример
- Что характеризует показатель IRR и как сопоставлять его с другими финансовыми показателями
- Может ли irr быть больше 100. Определение внутренней нормы доходности для оценки привлекательности проекта
- Определение
- Зачем нужен расчет?
- Формула и пример
- Расчет в Excel
- Анализ результата
- О точности расчета ставки дисконтирования
- Внутренняя ставка доходности IRR (ВСД)
- Расчет NPV при постоянных денежных потоках с помощью функции ПС()
- Внутренняя ставка доходности ЧИСТВНДОХ()
- Чистый дисконтированный доход (NPV)
- Расчет дисконтированного дохода (PV)
- Расчет чистого дисконтированного дохода (NPV)
- Внутренняя норма доходности (IRR)
- Пример определения NPV в Excel
- Норма доходности: предварительные сведения
- Что такое внутренняя норма доходности
- Пример расчета внутренней нормы доходности
IRR: формула расчета, экономический смысл
Статья рассматривает особенности расчета и используемую формулу показателя IRR. Также в статье описан экономический смысл IRR, и что характеризует данный показатель.
Определение и формула внутренней нормы доходности IRR
Внутренняя норма доходности IRR – (с английского — Internal Rate of Return), один из главных показателей, используемых при оценке привлекательности того или иного инвестиционного проекта.
Что же представляет из себя показатель IRR – это такая процентная ставка, при применении которой в качестве коэффициента дисконтирования, в формуле расчета чистого дисконтированного дохода, ЧДД будет равен нулю. Если говорить проще, то это определенная граница окупаемости инвестиций, по аналогии с точкой безубыточности компании. При таком значении ставки процента дисконтирования, финансовая организация или частный инвестор смогут гарантировано возвратить свои вложения, с нулевой прибылью.
Формула и примеры расчета IRR позволят понять специфику определения этого показателя.
Общий вид формулы расчета IRR:
- r — процентная ставка;
- NPV – чистый дисконтированный доход.
Изучим пример расчета IRR:
- требуемые инвестиции для реализации проекта – 1 000 000 руб.;
- доходность первого года – 100 000 руб.;
- второго года – 150 000 руб.;
- третьего года – 200 000 руб.;
- последнего – 270 000 руб.
Далее последовательно приближаемся к определению величины внутренней нормы доходности, в несколько шагов.
- Вычисление минимального значения IRR, по формуле:
- N — длительность проекта, в годах;
- IC — первоначально вложенный капитал;
- ∑ — сумма доходов за каждый год, приведенная к тысячам рублей.
После произведения нехитрых вычислений, получаем значение IIR равное 10% — это минимальная границы внутренней нормы прибыли для рассматриваемого проекта
- Далее надо посчитать максимальное значение IRR:
Получим значение IRR по максимальной границе, равное 44%. Эти значения говорят о том, что внутренняя норма доходности проекта должны находиться в диапазоне от 10% до 44%.
- Затем, надо определить предельные значения чистых дисконтированных доходов NPV, на основе предельных показателей IRR:
- На последнем этапе расчета IRR, производим его, с использованием всех ранее полученных данных:
Что характеризует полученный показатель IRR в 23%. Это та максимальная доходность, которую обеспечит проект, то есть, если условия предоставления капитала содержат ставки, выше рассчитанной IRR, то предприниматель не сможет вернуть его и получить прибыль. И наоборот, все источники финансирования, стоимость привлечения которых составляет менее 23% потенциально способны обеспечить прибыльность проекта.
IRR или внутренняя норма доходности – один из составляющих элементов сложной системы оценки инвестиционных проектов, позволяющий определить ставки, под которые предприниматель может привлекать капитал. И от корректности финансовых показателей зависит будущее проекта, поэтому скачивайте с нашего сайта полноценный готовый бизнес-план, включающий расчеты основных экономических и финансовых показателей. Или заказывайте индивидуальный бизнес-план «под ключ», полностью раскрывающий потенциал ваших предпринимательских талантов и организуемой компании.
Экономический смысл IRR
Чтобы раскрыть экономический смысл IRR, важно понимать, какие моменты он характеризует:
- Величина прибыли с осуществленного вложения капитала. Инвестор в процессе выбора из нескольких альтернативных проектах, при прочих равных, выберет тот, для которого значение IRR выше.
- Безубыточная кредитная ставка или стоимость привлечения финансовых средств на реализацию проекта. Это означает, что IRR – это своего рода граница, максимальная ставка стоимости использования заемного капитала, которая позволяет сделать проект безубыточным. Соответственно, если предприниматель берет кредит на открытие своего дела по ставке, большей, чем полученный IRR, он заранее обеспечивает себе потенциальные убытки.
Помимо экономического смысла, важно понимать, какие достоинства и недостатки несет использование показателя внутренней нормы доходности в качестве критерия оценки инвестиционных проектов.
Плюсы, которые делают использование IRR эффективным:
- возможность выбора между несколькими проектами в рамках новых или существующих предприятий. Чем больше значение внутренней нормы доходности, тем больше прибыли можно извлечь, обеспечив привлечение более дешевого по стоимости кредита или инвестиционного капитала;
- показатель позволяет сравнить несколько проектов с различными периодами инвестирования, отличающимися продолжительностью по времени. Соответственно, инвестор или кредитная организация выберет тот проект, который позволит больше заработать на капитале в долгосрочной перспективе.
Недостатки и минусы использования внутренней нормы доходности:
- невозможность на 100% точного прогнозирования величины выплат по вложенному капиталу;
- показатель IRR достаточно прост по структуре и не учитывает большое количество факторов внутренней и внешней среды, которые могут существенно повлиять на доходность проекта.
- отсутствие инструмента расчета суммы притока денег в абсолютном выражении, так как IRR, как относительный показатель, характеризует только ту процентную ставку, до которой вложения капитала остаются прибыльными.
- в расчете не учитываются возможные процессы реинвестирования;
- расчет IRR не предусматривает возможность учета тех прибылей, которые включаются в инвестиционные затраты за счет процентных доходов от их использования, что дает не совсем точную оценку номы доходности проекта.
Также обратите внимание на PBP инвестиционного проекта с формулой расчета показателя. Этот индикатор поможет вам еще более четко оценить все перспективы и возможности вашего проекта.
Расчет IRR в Excel пример
Современные средства автоматизации, различные табличные редакторы позволяют существенно упростить расчеты в рамках любых экономических процессов и моделей. Расчет IRR в Excel позволит ускорить и повысить точность вычислений, за счет использования встроенного редактора формул, содержащего и финансовый блок инструментов.
Основная функция, которая будет использоваться при расчете IRR в Excel – это ВСД (внутренняя ставка дисконта). Для доступа к ней нужно выбрать пункт «Финансовые» в разделе с формулами и найти описанную функцию.
Для того, чтобы рассчитать внутреннюю норму доходности, надо сформировать таблицу с данными, которые будут выступать в качестве параметров функции. Столбец таблицы заполняется значениям доходности инвестиций используется в качестве входных параметров для расчета IRR в Excel. Формулу завязываем на определенную ячейку и получаем гибкий инструмент расчета нескольких вариантов внутренней нормы доходности.
Ограничения использования Excel для расчета IRR:
- исходные данные должны содержать как минимум одно отрицательное значение показателя доходности – обычно это первый период реализации проекта, когда предприятие еще не получает выручки для формирования прибыли;
- периоды должны следовать строго последовательно, в соответствии с реально используемыми примерами и периодичностью вложений;
- если используется метод итераций, следует заполнять поле «Предположение» для осуществления корректных расчетов.
Что характеризует показатель IRR и как сопоставлять его с другими финансовыми показателями
Как уже было описано, IRR используется для оценки привлекательности инвестиционных проектов, с точки зрения максимальной ставки привлечения средств на его реализацию, чем ниже реальная ставка – тем больше прибыльность проекта.
На практике, показатель внутренней нормы доходности используется в совокупности и сравнении с другими, одним из которых является средневзвешенная стоимость капитала (WACC).
Соответственно, в зависимости от отношения этих индикаторов, оценивается привлекательность проекта:
- если IRR больше WACC, то потенциальная ставка доходности выше, чем предполагаемые затраты на формирование собственного и заемного капитала, что характеризует достаточно высокую инвестиционную привлекательность бизнеса;
- если IRR меньше WACC, то ситуация обратна первому положению – внутренняя норма доходности не позволяет окупить затраты на собственный и заемный капитал, следовательно – реализация проекта бесперспективна;
- IRR = WACC =- ситуация достаточно редкая и требует незначительных настроек проекта, чтобы обеспечить хотя бы минимальную доходность, за счет корректировок движения денежных средств в сторону их увеличения;
- если IRR одного проекта превышает IRR другого, очевидно, чтоб привлекательнее финансирование первого.
Аналогично описанным ситуациям, сравнение показателя внутренней нормы доходности можно проводить с другими показателями – ставками процентов по кредитам и вкладам, стоимости обслуживания инвестиций и т.д., чтобы получить возможность сопоставить проекты.
Наша компания занимается разработкой бизнес-планов на разные тематики. Так, вы можете заказать у нас, например, типовой бизнес-план из отрасли розничных продаж одежды и обуви или любой вопрос в зависимости от ваших предпочтений.
Обеспечение достаточной для получения прибыли нормы внутренней доходности – важная задача планирования, решение которой позволит защитить выгодность вложений в проект и привлечь внешнее финансирования. От профессионализма проектирования зависит многое, и стоит доверить этот процесс квалифицированным специалистам. У нас на сайте вы можете скачать готовый полноценный структурированный бизнес-план, с основными расчетами финансовых и экономических показателей эффективности проекта. Он позволит в короткие сроки открыть свое дело и занять достойную долю рынка. Также у вас есть возможность заказать индивидуальный бизнес-план «под ключ», в котором будет полностью раскрыта специфика организации и развития бизнеса конкретного предприятия или компании в определенной сфере экономической деятельности.
Источник
Может ли irr быть больше 100. Определение внутренней нормы доходности для оценки привлекательности проекта
В финансовом анализе прибыльности инвестиций особое место занимает внутренняя норма доходности. Расчёт показателя рекомендуется проводить всем организациям перед выбором инвестиционного проекта.
О процессе его вычисления и анализа и пойдет речь в данной статье.
Определение
Внутренняя норма доходности (ВНД) представляет собой определённую ставку, обеспечивающую отсутствие убытков по вкладам, тождественность доходов от инвестиции затратам на этот же проект . Иными словами, это то предельное значение процента, при котором разница между притоком и оттоком денег, то есть чистая приведённая стоимость (ЧПС), равна нулю.
Рассчитывать этот показатель удобнее всего при помощи специальных программ, например, Excel. Также можно использовать финансовый калькулятор.
Без применения автоматизированных методов вычисления определять процент величины придётся путём длительных расчётов. При этом определяется размер чистой приведённой стоимости при различных ставках дисконта. Такой способ называется методом итераций .
Например, ЧПС при ставке в 15% больше нуля и отрицательная при 5. Можно сделать вывод, что ВНД находится в диапазоне ставок от 5 до 15%. Далее меньшее число постоянно увеличивается и вычисление повторяется до тех пор, пока ЧПС не будет равняться нулю.
Зачем нужен расчет?
Экономический смысл показателя состоит в том, что он характеризует следующие моменты:
- Прибыльность возможного вложения . Когда предприятие выбирает, в какой проект произвести инвестиции, оно ориентируется на величину этого показателя. Чем больше размер ВНД, тем выше рентабельность вложений.
- Оптимальная ставка кредита . ВНД — это максимальная цена, при которой вложение остаётся безубыточным. Если компания планирует получить кредит на осуществление этой инвестиции, то следует обратить внимание на ставку годовых. Если процент по кредиту больше, чем полученное значение, то проект будет приносить убыток.
При использовании показателя для оценки будущих вложений нужно учитывать преимущества и недостатки этого метода.
К положительным моментам применения ВНД относятся:
- Сравнение возможных вложений между собой по эффективности использования капитала. Предприятие предпочтёт выбрать ту инвестицию, у которой при равной процентной ставке показатель больше.
- Сравнение проектов с разным горизонтом инвестирования, то есть временным периодом, на который осуществляется вложение. В данном случае при сопоставлении ВНД разных возможных вкладов выявляется тот, который будет приносить наибольшие доходы в долгосрочной перспективе.
К основным недостаткам и отрицательным чертам относят:
- Сложность прогнозирования выплат. С помощью расчёта данной величины нельзя предсказать, каков будет размер следующего поступления по вкладу. На размер прибыли влияет множество различных факторов, рисков, ситуаций на микро и макроэкономическом уровне, которые не учитываются при вычислении.
- Невозможно определить абсолютную величину притока денег. ВНД — относительный показатель, он уточняет только тот процент, при котором вклад всё ещё остаётся безубыточным.
- Не учитывается реинвестирование. Некоторые вклады предполагают включение в состав процентных отчислений. То есть происходит процесс наращивания суммы инвестиции за счёт прибыли с неё. Расчёт ВНД не предусматривает такую возможность, поэтому показатель не отражает реальную доходность этих затрат.
Формула и пример
Для определения способа вычисления ВНД используется уравнение:
- NPV — размер ЧПС;
- IC — начальная сумма инвестиций;
- CFt — приток денег за временной период;
- IRR — внутренняя норма доходности.
Учитывая это уравнение, можно определить, что показатель рассчитывается по следующей формуле:
Где r — процентная ставка.
Чтобы лучше понять, как рассчитать ВНД, нужно рассмотреть пример. Пусть проект требует вложений в 1 млн руб. По данным предварительного прогноза, в первый год доход будет составлять 100 тыс. руб, во второй — 150 тыс. руб., в третий — 200 тыс. руб., в четвёртый — 270 тыс. руб.
Расчёт показателя без применения специальных программ нужно производить методом итераций. Для этого нужно выполнить ряд действий:
Полученные данные свидетельствуют, что наибольшей годовой ставкой кредита, взятого для вклада, является 23%.
Если организация получит обязательства по выплате займа со ставкой более установленной величины, то проект будет убыточным. Предприятию желательно найти более выгодные условия.
Расчет в Excel
Расчёт показателя проще всего сделать, используя автоматизированные средства, например, Excel. В этой программе существуют встроенные финансовые формулы, позволяющие произвести вычисление очень быстро.
Для расчёта величины имеется функция ВСД . Однако эта формула будет корректно действовать только при наличии в таблице минимум одной положительной и одной отрицательной величины.
Формула в итоговой ячейке выглядит так: =ВСД(E3:E12) .
Порядок расчета в данной программе вы можете посмотреть на следующем видео:
Анализ результата

Показатель ССК характеризует минимальную величину доходов предприятия, которая может обеспечить учредителям возврат средств, потраченных на вклады в капитал. На основании этой цифры принимается большинство инвестиционных решений.
Также часто за показатель прибыльности принимают процентную ставку по кредитам. Такой метод позволяет выяснить, эффективно ли для данного проекта привлечение заёмных средств.
Целесообразность вкладов предприятие определяется исходя из соотношения ВСД и показателя прибыльности (П):
- ВСД=П . Это значит, что инвестиция находится на предельно допустимом уровне. Чтобы обеспечить эффективность затрат, следует пересмотреть первоначальную стоимость вложений, скорректировать потоки, сроки. Также при анализе инвестиций используется их сравнительный анализ.
- ВСД>П . Такое соотношение свидетельствует о том, что инвестиция покроет затраты на её обеспечение. Это вложение можно рассматривать как возможное, окончательное решение следует выносить, проведя дальнейший финансовый анализ.
- ВСД 0 (проект/ инвестиция окупается). В противном случае NPV файл примера, лист NPV ).
В таблице NPV подсчитан двумя способами: через функцию ЧПС() и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.)
Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода.
Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции ЧПС() , а нужно просто прибавить к получившемуся результату (см. файл примера ).
Сравнение 2-х вариантов дисконтирования приведено в файле примера , лист NPV:
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).
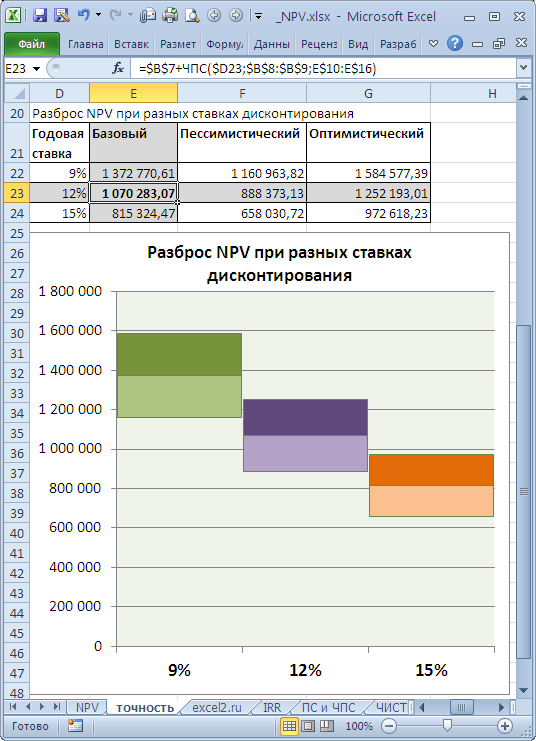
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа).
Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны.
Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера.
Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности IRR (ВСД)
Внутренняя ставка доходности (англ. internal rate of return , IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см. файл примера, лист IRR ).
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
Для расчета IRR используется функция ВСД() (английский вариант – IRR()). Эта функция тесно связана с функцией ЧПС() . Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией ВСД() , всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:
=ЧПС(ВСД(B5:B14);B5:B14)
Примечание4 . IRR можно рассчитать и без функции ВСД() : достаточно иметь функцию ЧПС() . Для этого нужно использовать инструмент (поле «Установить в ячейке» должно ссылаться на формулу с ЧПС() , в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Внутренняя ставка доходности ЧИСТВНДОХ()
По аналогии с ЧПС() , у которой имеется родственная ей функция ВСД() , у ЧИСТНЗ() есть функция ЧИСТВНДОХ() , которая вычисляет годовую ставку дисконтирования, при которой ЧИСТНЗ() возвращает 0.
Расчеты в функции ЧИСТВНДОХ() производятся по формуле:
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).
Примечание5 . Функция ЧИСТВНДОХ() используется для .
Для оценки эффективности планируемых инвестиций предприниматели рассматривают ряд важнейших экономических показателей, таких как срок окупаемости, чистый доход, потребность в дополнительном капитале, финансовая устойчивость и т.д. Одним из ключевых среди них является индикатор под названием внутренняя норма доходности. Давайте остановимся на ней подробней.
Внутренняя норма доходности часто обозначается через сокращение IRR. Этот термин означает максимальную стоимость инвестиций, при которой вложение денег в проект останется выгодным. Другими словами, внутренняя норма доходности — это средняя величина дохода на вложенный капитал, которую обеспечит данный проект. Данный параметр базируется на методе дисконтирования денежных потоков и позволяет принять верное решение относительно целесообразности инвестирования.
Формула расчета и трактовка
Внутренняя норма доходности IRR определяется из следующего равенства:
FCF 1 /(1+IRR) + FCF 2 /(1+IRR) 2 + FCF 3 /(1+IRR) 3 + … + FCF t /(1+IRR) t — Initial Investment = 0, где
FCF t — приведенный к настоящему моменту денежный поток за период времени t,
Initial Investment — первоначальные инвестиции.
Данный коэффициент рассчитывают методом последовательной подстановки в формулу такого значения дисконтной ставки, при которой общая приведенная стоимость прибыли от планируемых инвестиций будет соответствовать стоимости этих инвестиций, т.е. показатель NPV равен 0. Как правило, внутренняя норма доходности проекта определяется либо с помощью графика, либо посредством специализированных программ. В первом случае, на сетке координат отображают зависимость NPV от уровня ставки дисконтирования, а во втором — для нахождения IRR обычно используют MS Excel, в частности формулу =ВНДОХ(). Полученное значение сравнивают с ценой источника капитала (если планируется взять кредит в банке), либо просто с процентом по депозитному вкладу. Обозначим стоимость авансированного капитала через СС (capital cost). В результате сравнения может возникнуть один из трех вариантов:
Для начала возьмем простенький пример. Предположим, что на реализацию проекта потребуется первоначально затратить 100 000 грн. Спустя год величина чистой приведенной прибыли составит 127 000 грн. Давайте посчитаем, какая в этом случае получится внутренняя норма доходности: 130 000 / (1 + IRR) — 100 000 = 0. Решив его, получим, что искомый коэффициент равен: 127 000: 100 000 — 1 = 0,27, или 27%. Теперь возьмем пример посложнее. Предположим, что первоначальные инвестиции составят 90 000 руб, дисконтная ставка находится на уровне 10%, а денежные потоки распределяются по времени следующим образом (данные в тыс. грн.):
- 1 год — 48,4
- 2 год — 54,5
- 3 год — 67,3
- 4 год — 20,4
- 5 год — убыток 70,4
- 6 год — 30,2
- 7 год — 55,9
- 8 год — убыток 20,1
Чему будут равны в таком случае NPV и IRR? Здесь нам потребуется Excel. Скопируем наши данные в верх нового листа:
Поместим в ячейку А4 значение 0,1 — ставку дисконта. Для расчета NPV используем формулу: =ЧПС(A4;С2:J2)+B2. Обратите внимание, что первоначальные инвестиции мы не дисконтируем, поскольку они сделаны в начале года. Если бы они производились в течение первого года, тогда ячейку B2 тоже нужно было бы включать в диапазон расчёта. Однако для получения суммарной величины свободных денежных потоков мы обязательно должны прибавить эту величину. Итак, в долю секунды получаем, что NPV = 146,18 — 90 = 56,18. IRR рассчитывается еще проще. Поскольку данные в нашем примере поступали регулярно, то вместо формулы =ВНДОХ(), требующей указания дат, мы можем использовать функцию =ВСД(). Итак, вставим в свободную ячейку выражение = ВСД (B2:J8) и мгновенно получаем, что внутренняя норма прибыльности равна 38%.
Рассмотрим анализ инвестиционного проекта: рассчитаем основные ключевые показатели эффективности инвестиционного проекта. Среди ключевых показателей можно выделить два наиболее важных — NPV и IRR .
- NPV — чистый дисконтированный доход от инвестиционного проекта (ЧДД).
- IRR — внутренняя норма доходности (ВНД).
Рассмотрим данные показатели более детально и рассчитаем простой пример работы с ними в таблицах Excel.
Чистый дисконтированный доход (NPV)
NPV (Net Present Value , Чистый Дисконтированный Доход ) – пожалуй, один из наиболее популярных и распространенных показателей эффективности инвестиционного проекта. Рассчитывается он как разница между денежными поступлениями от проекта во времени и затратами на него с учетом дисконтирования.
Расчет чистого дисконтированного дохода (NPV):
- Определить текущие затраты на проект (сумма инвестиционных вложений в проект) — Io .
- Произвести расчет текущей стоимости денежных поступлений от проекта. Для этого доходы за каждый отчетный период приводятся к текущей дате (дисконтируются) — PV .
- Вычесть из текущей стоимости доходов (PV) наши затраты на проект (Io). Разница между ними будет чистый дисконтированный доход – NPV .
Расчет дисконтированного дохода (PV)
Расчет чистого дисконтированного дохода (NPV)
CF – денежный поток от инвестиционного проекта;
Iо — первоначальные инвестиции в проект;
r – ставка дисконта.
Показатель NPV – показывает инвестору доход/убыток от инвестирования денежных средств в инвестиционный проект. Данный доход он может сравнить с доходом в наименее рискованный вид активов — банковский вклад и рассчитать эффективность и целесообразность вложения в инвестиционный проект. Если NPV больше 0, то проект эффективен. После этого можно сравнить значение NPV с доходов от вклада в банк. Если NPV > вклад в наименее рискованный проект, то инвестиции целесообразны.
Формула чистого дисконтированного дохода (NPV) изменяется если инвестиционные вложения в проект осуществляются в несколько этапов (периодов) и имеет следующий вид.
CF – денежный поток;
r — ставка дисконтирования;
n — количество этапов (периодов) инвестирования.
Внутренняя норма доходности (IRR)
Внутренняя норма доходности (Internal Rate of Return , IRR ) – второй наиболее популярный показатель оценки инвестиционных проектов. Он определяет ставку дисконтирования, при которой инвестиции в проект равны 0 (NPV=0). Другими словами затраты на проект равны доходам от инвестиционного проекта.
IRR = r, при которой NPV = 0, находим из формулы:
CF – денежный поток;
It — сумма инвестиционных вложений в проект в t-ом периоде;
n — количество периодов.
Расчет IRR позволяет сравнить эффективность вложения в различные по протяженности инвестиционные проекты (по NPV это сделать нельзя). Данный показатель показывает норму доходности/возможные затраты при вложении денежных средств в проект (в процентах).
Пример определения NPV в Excel
Для наглядности рассчитаем расчет NPV в MS Excel. Для расчета NPV используется функция =ЧПС() .
Найдем чистый дисконтированный доход (NPV) инвестиционного проекта. Необходимые инвестиции в него — 90 тыс. руб. Денежный поток, которого распределен по времени следующим образом (как на рисунке). Ставка дисконтирования равна 10%.
Произведем расчет чистого дисконтированного дохода по формуле excel:
Где:
D3 – ставка дисконта.
C3 – вложения в 0 периоде (наши инвестиционные затраты в проект).
C4:C11 – денежный поток проекта за 8 периодов.
В итоге, показатель чистого дисконтированного дохода равен NPV=51,07 >0 , что говорит о том, что есть целесообразность вложения в инвестиционный проект. К примеру, если бы мы вложили 90 тыс. руб в банк со ставкой 10% годовых, то через год получили бы чуть меньше 9 тыс., что меньше чем 51,07 от вложения в инвестиционный проект.
Который вполне может посоперничать с за право считаться наиболее популярным отбора или отсеивания «неблагонадежных» инвестиционных .
Финансовые учебники весьма благосклонно оценивают данный показатель, рекомендуя его к широкому употреблению.
Задача сегодняшней публикации – с рентгеновской беспристрастностью расщепить на составляющие понятие внутренней нормы и предоставить заинтересованному читателю непредвзятый обзор преимуществ и недостатков данного метода, прежде всего, с точки зрения его практического применения.
Норма доходности: предварительные сведения
По традиции освежим в памяти некоторые важные правила, вытекающие из теории чистой .
В частности, одно из таких правил указывает на реализации инвестиционных возможностей, предлагающих большую , нежели размер наличествующих альтернативных издержек.
Сей тезис можно было бы признать абсолютно верным, если бы не многочисленные ошибки, связанные с его истолкованием.
Что такое внутренняя норма доходности
Когда заходит речь о нахождении истинной доходности долгосрочных инвестиций, многие и приходят в смятение, которое легко объяснимо.
Увы, простого и удобного инструмента, который позволял бы вручную, на коленках, без излишних умственных рассчитывать искомое значение, до сих пор не придумано…
Для решения этой задачи используется специальный , именуемый внутренней нормой доходности , который по сложившейся традиции обозначается как IRR .
Для вычисления этого показателя нужно решить «простейшее» уравнение:
Для случаев, когда T равно 1, 2 и даже 3, уравнение худо-бедно решаемо, и можно вывести относительно простые выражения, позволяющие рассчитать значение IRR посредством подстановки соответствующих данных.
Для случаев, когда T > 3, такие упрощения уже не проходят и на практике приходится прибегать к специальным вычислительным программам либо подстановкам.
Пример расчета внутренней нормы доходности
Теорию легче всего усваивать на конкретных примерах.
Представим, что размер наших первоначальных инвестиций составляет 1500 долл.
Денежный поток по истечении 1-го года будет равен 700 долл., 2-го года – 1400 долл., 3-го года – 2100 долл.
Подставив весь этот набор значений в нашу последнюю формулу, придадим уравнению следующий вид:
NPV = -1500 долл. + 700 долл. / (1 + IRR ) + 1400 долл. / (1 + IRR ) 2 + 2100 долл. / (1 + IRR ) 3 = 0.
Для начала рассчитаем значение NPV при IRR = 0:
NPV = -1500 долл. + 700 долл. / (1 + 0) + 1400 долл. / (1 + 0) 2 + 2100 долл. / (1 + 0) 3 = +2700 долл .
Поскольку мы получили ПОЛОЖИТЕЛЬНОЕ значение NPV, искомая внутренняя норма доходности тоже должна быть БОЛЬШЕ нуля.
Рассчитаем теперь значение NPV, скажем, при IRR = 80 % (0,80):
NPV = -1500 долл. + 700 долл. / (1 + 0,8) + 1400 долл. / (1 + 0,8) 2 + 2100 долл. / (1 + 0,8) 3 = -318,93 долл .
На этот раз мы получили ОТРИЦАТЕЛЬНОЕ значение. Это значит, что и внутренняя норма доходности должна быть МЕНЬШЕ 80 %.
Ради экономии времени мы самостоятельно рассчитали NPV при исходных данных для значений IRR , варьирующихся в пределах от 0 до 100, после чего построили следующий график:
Как следует из графика, при значении IRR , равном 60%, NPV будет равняться нулю (то есть пересекать ось абсцисс).
Попытки разыскать в недрах теории внутренней нормы доходности некий инвестиционный смысл приведут нас к следующим умозаключениям.
Если альтернативные издержки МЕНЬШЕ внутренней нормы доходности, инвестиции будут оправданными, и соответствующий проект следует ПРИНЯТЬ .
В противном случае от инвестиций следует ОТКАЗАТЬСЯ .
Обозрим наш график еще раз, чтобы понять, почему это действительно так.
Если значения ставки дисконтирования (размера альтернативных издержек) будут в пределах от 0 до 60, то есть быть МЕНЬШЕ внутренней нормы доходности, совокупность значений чистой приведенной стоимости будет ПОЛОЖИТЕЛЬНОЙ .
При равнозначности значений альтернативных издержек и внутренней нормы доходности, значение NPV окажется равным 0.
И, наконец, если величина альтернативных издержек ПРЕВЫСИТ размер внутренней нормы доходности, значение NPV будет ОТРИЦАТЕЛЬНЫМ .
Приведенные рассуждения верны для всех случаев, когда, как в нашем примере, график чистой приведенной стоимости имеет равномерно нисходящий вид .
На практике же возможны другие ситуации, разбор которых покажет нам, почему в конечном итоге использование метода внутренней нормы доходности, при прочих равных, может привести к ошибочным выводам в обоснованности инвестиционных решений.
Однако это уже тема наших последующих публикаций…
Источник