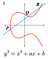Generate private key from public key bitcoin

How to Generate a Bitcoin Address — Step by Step

Here is a bash script that does what is outlined below: https://bit.ly/2MIgeOD

Introduction

This is a hands-on, technical guide about the generation of Bitcoin addresses including private and public keys, and the cryptography involved.

Learn more and join people in 22 countries around the world in my course on how to Become a Bitcoin + Blockchain Programmer.

This guide will walk you through all the steps to generate a Bitcoin address using the command line on a Mac. Similar steps should be possible on other operating systems using similar cryptographic tools. Lines starting with $ denote terminal commands, which you can type and run (without the $ of course).

Dependencies

• brew — Installation: https://brew.sh/
• pip — Installation: sudo easy_install pip
• libressl — Installation: brew install libressl
• base58 — Installation: pip install base58

Note: To do the contained openssl cli commands, I installed libressl in order for some of the elliptic curve commands to work as the current version of openssl cli on mac has a bug.

Cryptography Primer

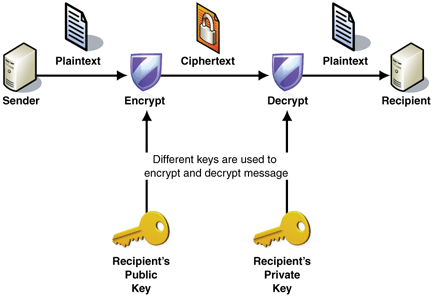
Public Key Cryptography

Or asymmetric cryptography, is a type of cryptography that uses key pairs, each of which is unique. The pair of keys includes a public key and a private key. This is the type of cryptography that Bitcoin uses to control funds. A public key can be generated from a private key, but not vice-versa (computationally too difficult). Also, something encrypted with a private key can be decrypted with the public key, and vice-versa, hence they are asymmetric.

• Encryption: When a user has a public key, a message can be encrypted using a public key, which can only be read by the person with the private key. This also works in reverse.
• Digital Signatures: A user can, with their private key and a hash of some data, use a digital signature algorithm such as ECDSA, to calculate a digital signature. Then, another user can use the algorithm to verify that signature using the public key and the hash of the same data. If it passes, this proves a user did in fact submit a specific message, which has not been tampered with.
• Digital Fingerprint: Is a way to represent an arbitrarily large data set by computing the hash of it to generate a fingerprint of a standard size. This fingerprint would be so difficult to replicate without the same exact data, which can be assumed to have not been tampered with.

Private keys are what prove you can send Bitcoin that has been sent to you. It is like the password to your bank account. If you lose it or someone else gets a hold of it, you’re toast.

Public keys help people know how to send you Bitcoin.

Creating a Bitcoin Address

Private Key Generation

Private keys can be any 256 bit (32 byte) value from 0x1 to 0xFFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF BAAE DCE6 AF48 A03B BFD2 5E8C D036 4140 .¹

The total possible number of private keys is therefore 2²⁵⁶ or 1.16 x 10⁷⁷. Imagine the total number of atoms in your body, then imagine that each of those atoms is an earth. The total number of atoms on all of those earths is about 7 x 10⁷⁷.² There is virtually no chance that your random private key will ever be generated randomly or found by someone else.

A common (but not the most secure) way of creating a private key is to start with a seed, such as a group of words or passphrases picked at random. This seed is then passed through the SHA256 algorithm, which will always conveniently generate a 256 bit value. This is possible because every computer character is represented by an integer value (see ASCII and Unicode).

Note: SHA256 is a one-way, deterministic function meaning that it is easy to compute in one direction, but you cannot reverse it. In order to find a specific output, you have to try all the possible inputs until you get the desired output (brute forcing) and it will always produce the same output given the same input, respectively.

The seed can be used to generate the same private key if the same hashing algorithm is used in the future, so it is only necessary to save the seed.

This private key is in hexadecimal or base 16. Every 2 digits represents 8 bits or 1 byte. So, with 64 characters, there are 256 bits total.

Public Key Generation

Public keys are generated from the private keys in Bitcoin using elliptic curve ( secp256k1 ) multiplication using the formula K = k * G , where K is the public key, k is the private key, and G is a constant called the Generator Point⁴, which for secp256k1 is equal to:

It doesn’t seem to be known how this point was chosen by they designers of the curve. Also, this algorithm is a one-way algorithm, or a “trap door” function so that a private key cannot be derived from the public key. It is important to note that elliptic curve multiplication is not the same as scalar multiplication, though it does share similar properties.

To do this in the terminal from our private key earlier,

This public key contains a prefix 0x04 and the x and y coordinates on the elliptic curve secp256k1 , respectively.

Compressed Public Key

Most wallets and nodes implement compressed public key as a default format because it is half as big as an uncompressed key, saving blockchain space. To convert from an uncompressed public key to a compressed public key, you can omit the y value because the y value can be solved for using the equation of the elliptic curve: y² = x³ + 7. Since the equation solves for y², the right side of the equation could be either positive or negative. So, 0x02 is prepended for positive y values, and 0x03 is prepended for negative ones. If the last binary digit of the y coordinate is 0, then the number is even, which corresponds to positive. If it is 1, then it is negative. The compressed version of the public key becomes:

The prefix is 0x02 because the y coordinate ends in 0xa4 , which is even, therefore positive.

Address Generation

There are multiple Bitcoin address types, currently P2SH or pay-to-script hash is the default for most wallets. P2PKH was the predecessor and stands for Pay to Public Key Hash. Scripts give you more functionality, which is one reason why they are more popular. We’ll first generate a P2PKH original format address, followed by the now standard P2SH .

The public key from the previous output is hashed first using sha256 and then hashed using ripemd160 . This shortens the number of output bytes and ensures that in case there is some unforeseen relationship between elliptic curve and sha256, another unrelated hash function would significantly increase the difficulty of reversing the operation:

Note that since the input is a string, the xxd -r -p will convert the hex string into binary and then output it in hexdump style (ascii), which is what the openssl hashing functions expect as input.

Now that we have hashed the public key, we now perform base58check encoding. Base58check allows the hash to be displayed in a more compact way (using more letters of the alphabet) while avoiding characters that could be confused with each other such as 0 and O where a typo could result in your losing your funds. A checksum is applied to make sure the address was transmitted correctly without any data corruption such as mistyping the address.

Bitcoin P2PKH addresses begin with the version byte value 0x00 denoting the address type and end with a 4 byte checksum. First we prepend the version byte (prefix) to our public key hash and calculate and append the checksum before we encode it using base58 :

Note: -c denotes a checksum is to be applied. The checksum is calculated as checksum = SHA256(SHA256(prefix+data)) and only the first 4 bytes of the hash are appended to the end of the data.

The resulting value is a P2PKH address that can be used to receive Bitcoin: 16JrGhLx5bcBSA34kew9V6Mufa4aXhFe9X

Pay-to-Script Hash

The new default address type is a pay-to-script-hash, where instead of paying to a pubKey hash, it is a script hash. Bitcoin has a scripting language, you can read more about it here. Basically it allows for things like multiple signature requirements to send Bitcoin or a time delay before you are allowed to send funds, etc. A commonly used script is a P2WPKH (Pay to Witness Public Key Hash): OP_0 0x14

where the PubKey Hash is the RIPEMD160 of the SHA256 of the public key, as before, and 0x14 is the number of bytes in the PubKey Hash. So, to turn this script into an address, you simply apply BASE58CHECK to the RIPEMD160 of the SHA256 of the script OP_0 0x14

except you prepend 0x05 to the script hash instead of 0x00 to denote the address type is a P2SH address.

If you like the article, check out my course on how to Become a Bitcoin + Blockchain Programmer.

Источник

How to generate your very own Bitcoin private key

In cryptocurrencies, a private key allows a user to gain access to their wallet. The person who holds the private key fully controls the coins in that wallet. For this reason, you should keep it secret. And if you really want to generate the key yourself, it makes sense to generate it in a secure way.

Here, I will provide an introduction to private keys and show you how you can generate your own key using various cryptographic functions. I will provide a description of the algorithm and the code in Python.

Do I need to generate a private key?

Most of the time you don’t. For example, if you use a web wallet like Coinbase or Blockchain.info, they create and manage the private key for you. It’s the same for exchanges.

Mobile and desktop wallets usually also generate a private key for you, although they might have the option to create a wallet from your own private key.

So why generate it anyway? Here are the reasons that I have:

• You want to make sure that no one knows the key
• You just want to learn more about cryptography and random number generation (RNG)

What exactly is a private key?

Formally, a private key for Bitcoin (and many other cryptocurrencies) is a series of 32 bytes. Now, there are many ways to record these bytes. It can be a string of 256 ones and zeros (32 * 8 = 256) or 100 dice rolls. It can be a binary string, Base64 string, a WIF key, mnemonic phrase, or finally, a hex string. For our purposes, we will use a 64 character long hex string.

The same private key, written in different formats.

Why exactly 32 bytes? Great question! You see, to create a public key from a private one, Bitcoin uses the ECDSA, or Elliptic Curve Digital Signature Algorithm. More specifically, it uses one particular curve called secp256k1.

Now, this curve has an order of 256 bits, takes 256 bits as input, and outputs 256-bit integers. And 256 bits is exactly 32 bytes. So, to put it another way, we need 32 bytes of data to feed to this curve algorithm.

There is an additional requirement for the private key. Because we use ECDSA, the key should be positive and should be less than the order of the curve. The order of secp256k1 is FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141 , which is pretty big: almost any 32-byte number will be smaller than it.

Naive method

So, how do we generate a 32-byte integer? The first thing that comes to mind is to just use an RNG library in your language of choice. Python even provides a cute way of generating just enough bits:

Looks good, but actually, it’s not. You see, normal RNG libraries are not intended for cryptography, as they are not very secure. They generate numbers based on a seed, and by default, the seed is the current time. That way, if you know approximately when I generated the bits above, all you need to do is brute-force a few variants.

When you generate a private key, you want to be extremely secure. Remember, if anyone learns the private key, they can easily steal all the coins from the corresponding wallet, and you have no chance of ever getting them back.

So let’s try to do it more securely.

Cryptographically strong RNG

Along with a standard RNG method, programming languages usually provide a RNG specifically designed for cryptographic operations. This method is usually much more secure, because it draws entropy straight from the operating system. The result of such RNG is much harder to reproduce. You can’t do it by knowing the time of generation or having the seed, because there is no seed. Well, at least the user doesn’t enter a seed — rather, it’s created by the program.

In Python, cryptographically strong RNG is implemented in the secrets module. Let’s modify the code above to make the private key generation secure!

That is amazing. I bet you wouldn’t be able to reproduce this, even with access to my PC. But can we go deeper?

Specialized sites

There are sites that generate random numbers for you. We will consider just two here. One is random.org, a well-known general purpose random number generator. Another one is bitaddress.org, which is designed specifically for Bitcoin private key generation.

Can random.org help us generate a key? Definitely, as they have service for generating random bytes. But two problems arise here. Random.org claims to be a truly random generator, but can you trust it? Can you be sure that it is indeed random? Can you be sure that the owner doesn’t record all generation results, especially ones that look like private keys? The answer is up to you. Oh, and you can’t run it locally, which is an additional problem. This method is not 100% secure.

Now, bitaddress.org is a whole different story. It’s open source, so you can see what’s under its hood. It’s client-side, so you can download it and run it locally, even without an Internet connection.

So how does it work? It uses you — yes, you — as a source of entropy. It asks you to move your mouse or press random keys. You do it long enough to make it infeasible to reproduce the results.

The process of generation an entropy by randomly moving the mouse. The large chunk of symbols shows the pool.

Are you interested to see how bitaddress.org works? For educational purposes, we will look at its code and try to reproduce it in Python.

Quick note: bitaddress.org gives you the private key in a compressed WIF format, which is close to the WIF format that we discussed before. For our purposes, we will make the algorithm return a hex string so that we can use it later for a public key generation.

Bitaddress: the specifics

Bitaddress creates the entropy in two forms: by mouse movement and by key pressure. We’ll talk about both, but we’ll focus on the key presses, as it’s hard to implement mouse tracking in the Python lib. We’ll expect the end user to type buttons until we have enough entropy, and then we’ll generate a key.

Bitaddress does three things. It initializes byte array, trying to get as much entropy as possible from your computer, it fills the array with the user input, and then it generates a private key.

Bitaddress uses the 256-byte array to store entropy. This array is rewritten in cycles, so when the array is filled for the first time, the pointer goes to zero, and the process of filling starts again.

The program initiates an array with 256 bytes from window.crypto. Then, it writes a timestamp to get an additional 4 bytes of entropy. Finally, it gets such data as the size of the screen, your time zone, information about browser plugins, your locale, and more. That gives it another 6 bytes.

After the initialization, the program continually waits for user input to rewrite initial bytes. When the user moves the cursor, the program writes the position of the cursor. When the user presses buttons, the program writes the char code of the button pressed.

Finally, bitaddress uses accumulated entropy to generate a private key. It needs to generate 32 bytes. For this task, bitaddress uses an RNG algorithm called ARC4. The program initializes ARC4 with the current time and collected entropy, then gets bytes one by one 32 times.

This is all an oversimplification of how the program works, but I hope that you get the idea. You can check out the algorithm in full detail on Github.

Doing it yourself

For our purposes, we’ll build a simpler version of bitaddress. First, we won’t collect data about the user’s machine and location. Second, we will input entropy only via text, as it’s quite challenging to continually receive mouse position with a Python script (check PyAutoGUI if you want to do that).

That brings us to the formal specification of our generator library. First, it will initialize a byte array with cryptographic RNG, then it will fill the timestamp, and finally it will fill the user-created string. After the seed pool is filled, the library will let the developer create a key. Actually, they will be able to create as many private keys as they want, all secured by the collected entropy.

Initializing the pool

Here we put some bytes from cryptographic RNG and a timestamp. __seed_int and __seed_byte are two helper methods that insert the entropy into our pool array. Notice that we use secrets .

Seeding with input

Here we first put a timestamp and then the input string, character by character.

Generating the private key

This part might look hard, but it’s actually very simple.

First, we need to generate 32-byte number using our pool. Unfortunately, we can’t just create our own random object and use it only for the key generation. Instead, there is a shared object that is used by any code that is running in one script.

What does that mean for us? It means that at each moment, anywhere in the code, one simple random.seed(0) can destroy all our collected entropy. We don’t want that. Thankfully, Python provides getstate and setstate methods. So, to save our entropy each time we generate a key, we remember the state we stopped at and set it next time we want to make a key.

Second, we just make sure that our key is in range (1, CURVE_ORDER ). This is a requirement for all ECDSA private keys. The CURVE_ORDER is the order of the secp256k1 curve, which is FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141 .

Finally, for convenience, we convert to hex, and strip the ‘0x’ part.

In action

Let’s try to use the library. Actually, it’s really simple: you can generate a private key in three lines of code!

You can see it yourself. The key is random and totally valid. Moreover, each time you run this code, you get different results.

Conclusion

As you can see, there are a lot of ways to generate private keys. They differ in simplicity and security.

Generating a private key is only a first step. The next step is extracting a public key and a wallet address that you can use to receive payments. The process of generating a wallet differs for Bitcoin and Ethereum, and I plan to write two more articles on that topic.

If you want to play with the code, I published it to this Github repository.

I am making a course on cryptocurrencies here on freeCodeCamp News. The first part is a detailed description of the blockchain.

I also post random thoughts about crypto on Twitter, so you might want to check it out.

Read more posts by this author.

If you read this far, tweet to the author to show them you care. Tweet a thanks

Learn to code for free. freeCodeCamp’s open source curriculum has helped more than 40,000 people get jobs as developers. Get started

freeCodeCamp is a donor-supported tax-exempt 501(c)(3) nonprofit organization (United States Federal Tax Identification Number: 82-0779546)

Our mission: to help people learn to code for free. We accomplish this by creating thousands of videos, articles, and interactive coding lessons — all freely available to the public. We also have thousands of freeCodeCamp study groups around the world.

Donations to freeCodeCamp go toward our education initiatives and help pay for servers, services, and staff.

Источник