- Routes to finance
- 7 Расчет окупаемости в коммерческой недвижимости (Июнь 2021).
- Проблема и формула будущей стоимости
- Будущая стоимость инвестиций с использованием финансового калькулятора
- Будущая стоимость инвестиций в суммарную сумму с использованием таблицы
- Формула расчета текущей стоимости инвестиций и денег в Excel
- Пример с расчетом текущей дисконтированной стоимости инвестиций в Excel
- Формула расчета текущей стоимости денег с учетом инфляции в Excel
- Как считать доходность инвестиций: формулы расчета
- Как рассчитать доходность инвестиций?
- Как считать доходность в процентах годовых?
- Как считать среднегодовую доходность
- Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Routes to finance
7 Расчет окупаемости в коммерческой недвижимости (Июнь 2021).
Инвестиции могут быть разнесены с течением времени — например, ежемесячное дополнение к вашему 401K, или, может быть, единовременная сумма инвестиций, например, покупка аннуитета. В последнем случае вы можете рассчитать будущую стоимость своих инвестиций, используя известную финансовую формулу, называемую «будущая стоимость единовременных инвестиций». Ниже приведены три разных способа решения проблемы. Каждый метод использует различные способы расчета, но базовая формула одинакова во всех трех случаях.
Проблема и формула будущей стоимости
Предположим, что у нас есть 100 долларов, а процентная ставка составляет 5%. Какова будет стоимость инвестиций в конце первого года? Формула для будущей стоимости этих инвестиций в единовременную сумму выглядит следующим образом:
FV 1 = PV + INT или PV (1 + I) ⁿ
Первая часть этого уравнения — FV₁ = PV + INT — гласит: «будущее значение ( FV ) в конце одного года — нижний индекс ᵢ — равен текущей стоимости плюс добавленная стоимость по указанной процентной ставке.
Следующая формула представляет это в форме, которую легче вычислить добавленная сумма накопленного интереса — PV (1 + I) ⁿ — , которая гласит: «текущее значение ( PV) раз (1 + I) ⁿ , где l представляет процентную ставку, а верхний индекс ⁿ — это количество периодов рецептуры.
Теперь давайте рассмотрим пример сверху. В течение одного года ваши единовременные инвестиции в размере $ 100, составляющие 5% в год, будут равны:
FV = $ 100 (1 + 0. 05) = $ 105
В этом случае вы не видите надстрочный индекс (n) для так как на данный момент вы решаете только на первый год.
Если вы хотите определить значение в конце двух лет, ваш расчет будет выглядеть следующим образом:
FV = $ 100 (1 + 0. 05) ² = $ 110. 25
Вы можете решить эту проблему, которая представляет собой сложную задачу, путем вычисления значения в конце первого года, а затем умножения результата на ту же 5-процентную ставку на второй год:
FV = [$ 100 (1 + 0. 05)] + [$ 105 (1 + 0. 05)] = $ 110. 25
Вы можете продолжить этот процесс, чтобы найти будущую стоимость инвестиций для любого количества периодов рецептуры.
Описывая этот процесс — вручную добавляя добавленную стоимость каждого года из интереса, а затем используя это значение для проведения аналогичных вычислений для каждого следующего года — дает понять, как мы достигаем результата, но это отнимает много времени , Решение о будущем значении 20 лет в будущем означает повторение математики 20 раз. Есть более быстрые и лучшие способы решения этой проблемы, одним из которых является использование финансового калькулятора.
Будущая стоимость инвестиций с использованием финансового калькулятора
Формула для определения будущей стоимости инвестиций в финансовый калькулятор:
Хотя это не совсем так, это та же самая формула, которую мы использовали, когда мы вручную делали расчеты.
Кстати, вы можете использовать эту формулу с любым калькулятором, который имеет экспоненциальный функциональный ключ — большинство из них. Однако использовать финансовый калькулятор лучше, потому что он имеет выделенные ключи, соответствующие каждой из четырех переменных, которые мы будем использовать, ускоряя процесс и минимизируя возможность ошибки. Вот клавиши, которые вы будете пробивать:
Punch N и 2 (в течение 2 лет)
Punch I / YR и 5 (для процентной ставки 5%)
Punch PV и -105 (за сумму, которую мы рассчитываем на проценты в год 2)
Punch PMT и PMT (нет платежей за пределами первого)
Punch FV , который возвращает ответ в $ 110. 25
Преимущество финансового калькулятора над ручным методом очевидно. С калькулятором, это не сложнее или трудоемко решить для будущей стоимости через 20 лет, чем решить в течение одного года. Другой метод экономии времени использует электронную таблицу.
Будущая стоимость инвестиций в суммарную сумму с использованием таблицы
Таблицы, такие как Microsoft Excel, хорошо подходят для расчета временной стоимости денежных проблем. Функция, которую мы используем для будущей стоимости инвестиции или единовременной суммы в электронной таблице Excel:
Чтобы использовать функцию на листе , нажмите «Формулы» в строке заголовка, затем нажмите «Финансовый». Затем вы увидите список функций. Нажмите FV. Это откроет окно построителя формул, в котором вы увидите пять полей с надписью rate, nper, pmt, pv и . Если вы хотите определить будущую стоимость в конце двух лет, заполните поля следующим образом:
ставка (процентная ставка) =. 05
nper (общее количество периодов оплаты = 2
pmt (повторные платежи, в этом случае нет) = 0
pv (текущее значение, выраженное как отрицательное число) = -100
type ( это относится к срокам последующих платежей) = Поскольку их нет, введите 0
Более ранние версии Excel требуют, чтобы вы щелкнули по Рассчитать , чтобы увидеть результат . результат автоматически.
Источник
Формула расчета текущей стоимости инвестиций и денег в Excel
Временная стоимость денег (Time Value of Money, TVM) – это важный показатель в бухгалтерской и финансовой отрасли. Идея заключается в том, что рубль сегодня стоит меньше чем тот же самый рубль завтра. Разница между этими двумя финансовыми значениями является прибыль, которую можно извлечь с одного рубля или убыток. Например, данная прибыль может быть получена с процентов, начисленных на банковском счете или в качестве дивидендов от инвестиций. Но также может быть убыток при оплате процентов за погашение кредитного долга.
Пример с расчетом текущей дисконтированной стоимости инвестиций в Excel
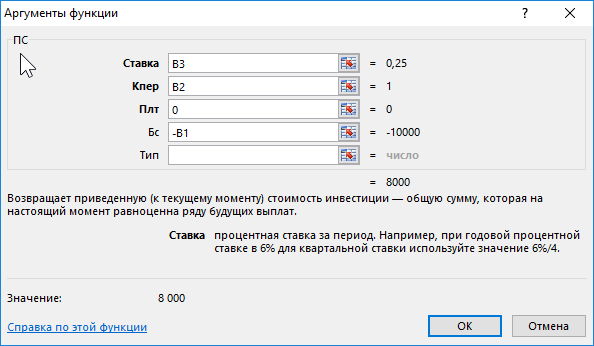
Программа Excel предлагает несколько финансовых функций для вычисления стоимости денег во времени. Например, функция ПС (приведенная стоимость) возвращает текущую стоимость инвестиций. Простыми словами, данная функция снижает сумму на размер процента дисконтирования и возвращает текущую стоимость для этой суммы. Если инвестиционный проект предполагает принести прибыль в размере 10 000 через год. Вопрос: какой максимальной суммой рационально рискнуть чтобы инвестировать в данных проект?
Например, в России розничный бизнес иногда делает прибыль до 35% годовых, а оптовый не более 15%. Учитывая небольшую сумму инвестиций предполагается, что инвестиционный объект не является оптовым бизнесом, а значит следует ожидать прибыль больше чем 15% годовых. Ниже на рисунке провиден пример формулы калькулятора доходности инвестиций в процентах:
Как мы видим на рисунке калькулятор нам отображает, чтобы получить сумму 10 000 за 1 год при доходности 25% нам необходимо вложить 8 000 финансовых средств. То есть если бы у нас была сумма 8 000 и мы вложили ее под 25% годовых через год мы заработали бы 10 000.
Функция ПС имеет 5 аргументов:
- Ставка – процентная ставка дисконтирования. Это прибыль в процентах, на которую можно рассчитывать за период дисконтирования. Это значение имеет наибольшее влияние на вычисление текущей стоимости инвестиций, но его наиболее сложно точно определить. Осторожные инвесторы чаще всего занижают процентную ставку до максимально реально достижимого уровня при тех или иных условиях. Если же финансовые средства предназначены для погашения кредита, в таком случае данный аргумент определяется легко.
- Количество периодов (Кпер) – период времени на протяжении которого дисконтируется будущая сумма. В данном примере указан 1 год (записанный в ячейке B2). Процентная ставка и количество лет должны быть выражены в соответственных единицах измерения. Это значит, что вы используете годовую ставку, тогда числовое значение в данном аргументе значит количество лет. Если указана процентная ставка в первом аргументе для месяцев (например, 2,5% ежемесячных), тогда число во втором аргументе значит количество месяцев.
- Платеж (Плт) – сумма, которая периодически платится на протяжении периода дисконтирования. Если предусмотрен в условиях инвестирования только один платеж, как в выше приведенном примере, тогда данная сумма является будущей стоимостью денег, а сам платеж равен =0. Данный аргумент должен быть согласован со вторым аргументом количества периодов. Если количество периодов дисконтирования равно 10, а третий аргумент не равен <>0, тогда функция ПС посчитает как 10 платежей на сумму, указанную в третьем аргументе (Плт). Ниже на следующем примере изображено как вычисляется текущая стоимость денег при нескольких взносах отдельными платежами.
- Будущая стоимость (БС) – это сумма, которую следует получить в конце периода дисконтирования. Финансовые функции Excel основаны на вычислениях наличного потока. Это значит, что будущая стоимость и текущая стоимость инвестиций имеют противоположные знаки чисел. В данном примере будущая стоимость является отрицательным числом, поэтому формула в результате вычислений возвращает положительное число.
- Тип – данный аргумент должен иметь значение 0, если выплата итоговой суммы припадает на конец периода дисконтирования, или число 1 – если на его начало. В данном примере значение данного аргумента не имеет значения и никак не повлияет на итоговый результат вычисления. Так как платежный взнос равен нулю и аргумент определяющий тип может быть опущен. В таком случае функция по умолчанию присваивает данному аргументу значение 0.
Формула расчета текущей стоимости денег с учетом инфляции в Excel
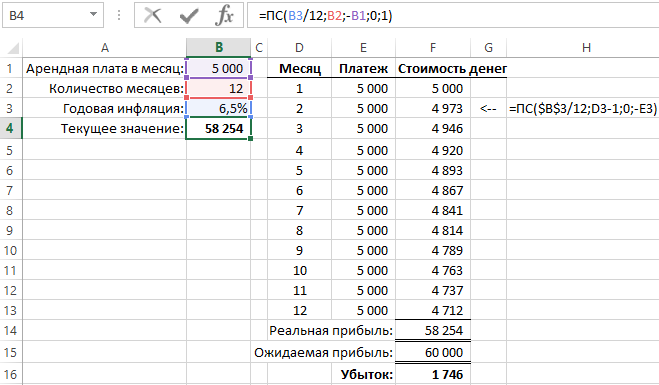
В другом примере применения функции ПС выполняется вычисление будущей стоимости денег сразу для целой серии будущих равных платежных взносов. Если, например, по договору аренды офиса арендатор должен платить по 5000 каждый месяц на протяжении одного года, тогда арендодатель с помощью функции ПС сможет посчитать сколько он потеряет дохода при учете 6,5% годовой инфляции:
В данном примере пятый аргумент «Тип» имеет числовое значение 1, так как оплата за аренду платится в начале каждого месяца.
В случае наличия суммы регулярных платежей функция ПС в реальности вычисляет текущую стоимость денег отдельно для каждого платежа и суммирует полученные результаты. На рисунке видны результаты вычисления стоимости для каждого платежа. Текущая стоимость первого платежа такая же, как и сумма платежа, так как платится сейчас по факту. Платеж в следующем месяце будет проплачен через месяц и уже уменьшается его текущая денежная стоимость (обесценивается). Он дисконтирован до суммы 4 973. Изменения не значительные, но последний платеж, который буде проплачен через 11 месяцев имеет стоимость уже существенно ниже – 4 712. Все результаты вычисления значений текущей стоимости инвестиций необходимо суммировать. Функция ПС выполняет всю эту работу автоматически без необходимости составления хронологического графика платежей за весь период.
Источник
Как считать доходность инвестиций: формулы расчета
Автор: Алексей Мартынов · Опубликовано 01.06.2015 · Обновлено 05.11.2015

Доходность (норма доходности, уровень доходности) — это степень увеличения (или уменьшения) инвестированной суммы за определенный период времени. В отличие от дохода, который выражается в номинальных величинах, то есть в рублях, долларах или евро, доходность выражается в процентах. Доход можно получать в двух видах:
- процентный доход — это проценты по депозитам, купоны по облигациям, дивиденды по акциям, арендная плата по недвижимости;
- рост стоимости купленных активов — когда цена продажи актива больше цены покупки — это акции, облигации, недвижимость, золото, серебро, нефть и другие товарные активы.
Такие активы как недвижимость, акции и облигации могут сочетать в себе два источника дохода. Расчет доходности нужен для оценки роста или падения вложений и является критерием оценки эффективности инвестиций.
Как рассчитать доходность инвестиций?
В общем виде доходность всегда рассчитывается как прибыль (или убыток), деленная на сумму вложенных средств, умноженная на 100%. Прибыль считается как сумма продажи актива — сумма покупки актива + сумма денежных выплат, полученных за период владения активом, то есть процентный доход.
Формула 1
Мы купили акцию по цене 100 рублей (сумма вложений), продали акцию по цене 120 рублей (сумма продажи), за период владения акцией получили 5 рублей дивидендов (денежные выплаты). Считаем доходность: (120-100+5)/100 = 0,25 ∗ 100% = 25%.
Формула 2
Есть вторая формула, по которой доходность считается как сумма продажи актива + сумма денежных выплат, деленная на сумму вложений, минус 1, умноженная на 100%.
Как считать доходность в процентах годовых?
В формуле расчета простой доходности не учитывается такой важный параметр, как время. 25% можно получить за месяц, а можно и за 5 лет. Как тогда корректно сравнить доходность активов, время владения которыми различается? Для этого считают доходность в процентах годовых. Доходность в процентах годовых рассчитывается для того, чтобы сравнить друг с другом эффективность активов, время владения которыми отличается. Доходность в процентах годовых — это доходность, приведенная к единому знаменателю — доходности за год.
К примеру банковский вклад дает 11% в год, а какие-то акции принесли 15% за 1,5 года владения ими, что было выгоднее? На первый взгляд акции, они ведь принесли доходность больше. Но инвестор владел ими больше на полгода, поэтому их доходность как бы растянута во времени по сравнению с депозитом. Поэтому, чтобы корректно сравнить депозит и акции, доходность акций нужно пересчитать в процентах годовых.
Для этого в формулу добавляется коэффициент 365/T, где Т — количество дней владения активом.
Мы купили акцию за 100 рублей, продали через 1,5 года за 115 рублей. 1,5 года это 1,5*365=547 дней.
(115-100)/100 ∗ 365/547 ∗ 100% = 10%. В этом случае депозит оказался немного выгоднее акций.
Как форекс, управляющие компании, брокеры и банки манипулируют годовой доходностью.
В любой рекламе доходности обращайте внимание на сноски, уточняйте какую доходность указывают в рекламе и за какой период. К примеру, в рекламе звучит доходность 48% годовых. Но она может быть получена всего лишь за один месяц. То есть компания за месяц заработала 4% и теперь с гордостью рекламирует продукт, дающий 4*12=48% годовых. Даже вы, заработав за день на бирже 1%, можете хвастаться, что заработали 365% годовых) Только доходность эта виртуальная.
 Как считать среднегодовую доходность
Как считать среднегодовую доходность
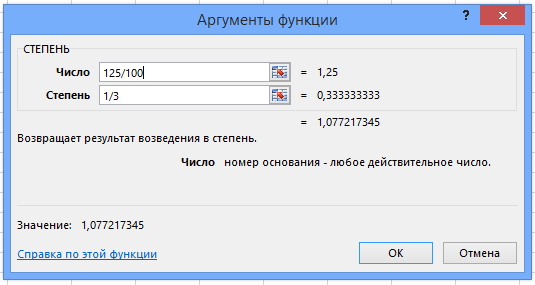
Срок владения активами может составлять несколько лет. При этом большинство активов не растет на одну и ту же величину. Такие активы как акции могут падать или расти на десятки или сотни процентов в год. Поэтому хочется знать, сколько в среднем в год росли ваши инвестиции. Как тогда вычислить среднюю годовую доходность? Среднегодовая доходность рассчитывается через извлечение корня по формуле:
Формула 1
где n — количество лет владения активом.
3√125/100 — 1 ∗ 100% = 7,72%
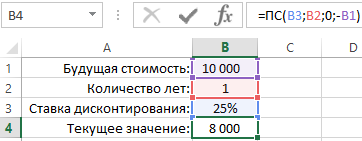
Формула 2
Другая формула расчета среднегодовой доходности — через возведение в степень.

Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Если известны доходности актива по годам, то среднюю годовую доходность можно вычислить перемножив годовые доходности и извлечь из произведения корень в степени равной количеству лет.
Для начала переведите доходности из процентов в числа.
Эти формулы учитывают эффект сложных процентов. Простая формула расчета доходности этого не учитывает и завышает доходность, что не совсем правильно.
Источник




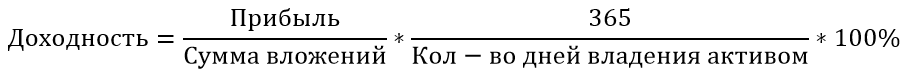
 Как считать среднегодовую доходность
Как считать среднегодовую доходность