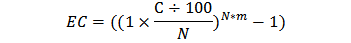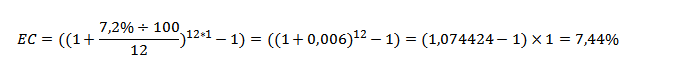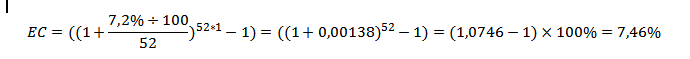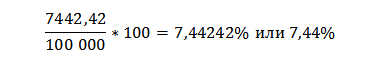- Эффективная ставка по вкладу
- Что такое эффективная ставка по вкладу?
- Зачем нужна эффективная ставка по вкладу, и чем она полезна для клиента?
- Формула расчета эффективной ставки.
- Как влияют на эффективную ставку операции пополнения вклада или частичного снятия.
- Эффективная процентная ставка
- Определение
- Формула
- Примеры расчета
- Пример 1
- Пример 2
- Пример 3
Эффективная ставка по вкладу
Банковские депозиты являются одним из инструментов инвестирования, который приносит гарантированный доход. Они являются самыми низкорисковыми и пассивными, поскольку не требуют вмешательства клиента, а получением прибыли занимается профессиональный участник – финансовая организация. Зачастую, рекламируется для клиентов ставка по вкладу, которая является номинальной, что в сути не отражает реальной прибыли. Эффективная ставка же по вкладу отражает реальную прибыльность вклада. Рассмотрим что это такое более подробнее.
Что такое эффективная ставка по вкладу?
Чтобы оценить настоящий доход, который можно получить от вложения своих денег на депозит, используется эффективная ставка. Она отражает прибыль клиента с учетом капитализации процентов во вклад и всегда будет выше номинальной ставки. Как показывает практика, доход от вклада с капитализацией имеет бОльшую прибыльность, чем вклад без капитализации.
Это происходит из-за того, что проценты при капитализации начисляются с выбранной периодичностью (в месяц, в квартал, в полугодие, в год) и суммируются к основному телу депозита.
Зачем нужна эффективная ставка по вкладу, и чем она полезна для клиента?
Она отражает общий доход за весь срок с учетом причисления процентов к вкладу. Это помогает клиенту оценить его реальный доход и сравнить условия по видам депозитов в одном или нескольких банках. Если владелец депозита желает получить максимальный доход, то ему следует выбирать вклады с ежемесячной капитализацией процентов. 
Как это работает? В первый месяц проценты начисляются на сумму вклада и присоединяются к нему. Во второй месяц проценты начисляются уже на сумму вклада+проценты за первый месяц. Следовательно, эта сумма уже будет больше, чем в первый месяц и т.д. В этом случае используется формула сложного процента, т.е. когда идет начисление процентов на увеличивающуюся сумму. Итоговая доходность будет выше исходной процентной ставки.
Формула расчета эффективной ставки.
Чтобы посмотреть наглядно, как идет начисление, нужно воспользоваться формулой расчета эффективного процента по депозиту:
- ЕС – это эффективная ставка по вкладу, т.е. значение доходности, которое получится при причислении процентов к основному телу вклада за определенный срок
- С – это номинальная ставка, т.е. то значение, которое обычно указывается в договоре
- N – это количество периодов капитализации в год (если ежемесячная капитализация, то N=12, если еженедельная, то N=52, если ежеквартальная, то N=4)
- m – это количество повторений периодов (если на один год, то m=1, если на два года, то m=2 и т.д).
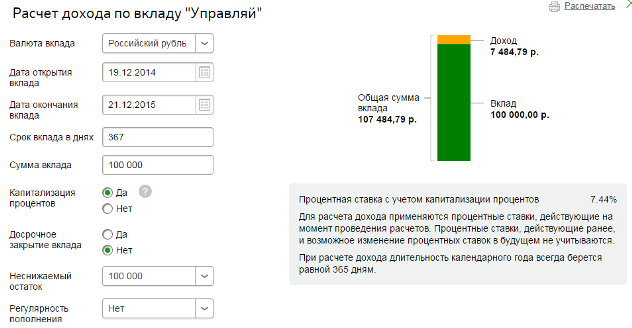
Просчитаем эффективную ставку по вкладу Сбербанка «Управляй» на 100 000 на один год с ежемесячным причислением процентов с номинальной ставкой 7,2%. Ниже представлен ручной расчет, но можно воспользоваться калькулятором депозитов, просто вбив параметры своего вклада.
Если бы депозит открыт на год, а проценты начислялись каждую неделю, то формула выглядела бы следующим образом (берем N=52, т.к. в году 52 недели):
Таким образом, если расположить 100 000 рублей на один год с капитализацией процентов ежемесячно, то эфф.ставка составит 7,44%, что на 0,24% больше номинала. Если капитализация будет производиться еженедельно, то эфф.ставка за год составит 7,46%.
Чтобы проверить это значение на практике, произведем расчет на примере этого же вклада (с ежемесячной капитализацией). Используем формулу для расчета %-ов:
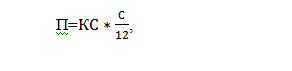
где
- П – сумма начисленных процентов за каждый месяц,
- КС – капитализированная сумма с учетом причисления процентов за предыдущий месяц,
- С – ставка номинальная.
| Месяцы | Кап.сумма, руб | Ставка в месяц | Проценты за месяц, руб |
|---|---|---|---|
| 1 | 100 000 | 0,006 | 600 |
| 2 | 100600 | 0,006 | 603,6 |
| 3 | 101203,6 | 0,006 | 607,22 |
| 4 | 101810,82 | 0,006 | 610,87 |
| 5 | 102421,69 | 0,006 | 614,53 |
| 6 | 103036,22 | 0,006 | 618,22 |
| 7 | 103654,43 | 0,006 | 621,93 |
| 8 | 104276,36 | 0,006 | 625,66 |
| 9 | 104902,02 | 0,006 | 629,41 |
| 10 | 105531,43 | 0,006 | 633,19 |
| 11 | 106164,62 | 0,006 | 636,99 |
| 12 | 106801,61 | 0,006 | 640,81 |
| Итого | 7442,42 |
Теперь рассчитаем эфф.ставку. Для этого разделим полученную сумму процентов на первоначальную сумму вклада:
| Месяцы | Кап.сумма, руб | Ставка в месяц | Проценты за месяц, руб |
|---|---|---|---|
| 1 | 100 000 | 0,006 | 600 |
| 2 | 100600 | 0,006 | 603,6 |
| 3 | 101203,6 | 0,006 | 607,22 |
| 4 | 101810,82 | 0,006 | 610,87 |
| 5 | 102421,69 | 0,006 | 614,53 |
| 6 | 103036,22 | 0,006 | 618,22 |
| 7 | 103654,43 | 0,006 | 621,93 |
| 8 | 104276,36 | 0,006 | 625,66 |
| 9 | 104902,02 | 0,006 | 629,41 |
| 10 | 105531,43 | 0,006 | 633,19 |
| 11 | 106164,62 | 0,006 | 636,99 |
| 12 | 106801,61 | 0,006 | 640,81 |
| Итого | 7442,42 |
Произведем расчет на калькуляторе Сбербанка:
Как видно из рисунка, суммы практически совпадают. Небольшое различие в 42 рубля связано с тем, что 19.12.2015 г. попадает на выходной день. Это значит, что дата закрытия переносится на следующий рабочий день – 21.12.2015 г.
Как влияют на эффективную ставку операции пополнения вклада или частичного снятия.
При пополнении вклада, его основное тело увеличивается, следовательно, клиент получит больше процентов.
Рассмотрим вариант, когда клиент вносит на третий месяц сумму в 20 000 руб.
| Месяцы | Кап.сумма, руб | Ставка в месяц | Проценты за месяц, руб |
|---|---|---|---|
| 1 | 100000 | 0,006 | 600 |
| 2 | 100600 | 0,006 | 603,6 |
| 3 | 121203,6 | 0,006 | 727,2216 |
| 4 | 121930,82 | 0,006 | 731,5849 |
| 5 | 122662,41 | 0,006 | 735,9744 |
| 6 | 123398,38 | 0,006 | 740,3903 |
| 7 | 124138,77 | 0,006 | 744,8326 |
| 8 | 124883,60 | 0,006 | 749,3016 |
| 9 | 125632,91 | 0,006 | 753,7974 |
| 10 | 126386,70 | 0,006 | 758,3202 |
| 11 | 127145,02 | 0,006 | 762,8701 |
| 12 | 127907,89 | 0,006 | 767,4474 |
| Итого | 8675,341 |
Итого, общая сумма процентов получится на 1233 руб. больше.
При частичном снятии суммы, итоговая прибыль уменьшится, следовательно, уменьшится и эфф. ставка.
Таким образом, значимое различие между номинальной и эффективной ставкой заметно, если вклад отлежал продолжительный промежуток времени, а капитализация производилась ежемесячно. Клиент сам вправе выбирать, что ему удобнее в той или иной ситуации.
Источник
Эффективная процентная ставка
Определение
Концепция эффективной процентной ставки (англ. Effective Interest Rate) используется для того, чтобы провести оценку всех затрат связанных с привлечением заемного финансирования или доходов от вложений в финансовый актив. Кроме того, требования МСФО (международных стандартов финансовой отчетности) предполагают использование эффективной процентной ставки при оценке финансовых инструментов, учитываемых по амортизированной стоимости, признании расходов и доходов по финансовым инструментам, расчете обесценения финансового актива на основе приведенной стоимости будущих денежных потоков.
Причина использования этой концепции при принятии решений заключается в том, что эффективная годовая процентная ставка может отличаться от номинальной годовой процентной ставки, указанной в договоре. Причиной несовпадения этих величин служат следующие факторы:
- количество периодов, за которое в течение года начисляются проценты;
- фактическая сумма уплаченных процентов;
- фактически понесенные расходы на выплату долга.
Формула
При проведении финансовых расчетов эффективная процентная ставка приводится к годовому формату и также может упоминаться как эффективная годовая процентная ставка или годовая эквивалентная ставка (англ. Annual Equivalent Rate).
Для оценки доходности краткосрочного финансового актива (срок обращения менее 12 месяцев) используется следующая формула:
где i – номинальная годовая процентная ставка, n – количество периодов, за которое в течение года начисляются проценты (например, если проценты начисляются ежемесячно, то n=12).
При оценке стоимости использования краткосрочного финансирования формулу эффективной годовой процентной ставки в общем виде можно записать следующим образом:
| r = | Проценты к уплате |
| Сумма кредита |
В случае дисконтного процента формула должна быть трансформирована следующим образом:
| r = | Проценты к уплате |
| Сумма кредита — Проценты к уплате |
При расчете эффективной процентной ставки также должны быть учтены следующие два фактора:
- Дополнительные расходы, которые по сути являются срытыми процентами.
- Условия, затрагивающие основную сумму долга. Например, наличие компенсационного остатка по кредиту уменьшает реальную располагаемую сумму.
В этом случае формулы выше должны быть скорректированы следующим образом:
| r = | Проценты к уплате + Дополнительные расходы |
| Сумма кредита — Компенсационный остаток |
Для дисконтного процента следует воспользоваться этой формулой:
| r = | Проценты к уплате + Дополнительные расходы |
| Сумма кредита — Проценты к уплате — Компенсационный остаток |
Примеры расчета
Пример 1
Предположим, что инвестор рассматривает возможность приобретения векселя за $9 655 со сроком погашения наступающим через четыре месяца и номиналом $10 000. В этом случае расчет эффективной годовой процентной ставки будет выглядеть следующим образом.
Проценты к получению = $10 000 — $9 655 = $345
| Ставка процента за 4 месяца = | $345 | = 3,573% |
| $9 655 |
Эффективная годовая процентная ставка = (1 + 0,03573) 12/4 — 1 = 11,107%
В этом случае мы привели наши расчеты к годовой эквивалентной ставке с учетом концепции сложных процентов.
Пример 2
Компания GFL LTD рассматривает различные варианты финансирования потребности в оборотном капитале в размере $100 000. Существует возможность взять банковский кредит на следующих условиях:
- период кредитования 1 год;
- номинальная годовая процентная ставка 12%;
- единовременная комиссия за рассмотрение кредитной заявки и открытие кредитного счета 2% от суммы кредита;
- компенсационный остаток $15 000.
Проценты к уплате = $100 000 × 12% = $12 000
Дополнительные расходы = $100 000 × 2% = $2 000
| Эффективная годовая процентная ставка = | $12 000 + $2 000 | = 16,471% |
| $100 000 — $15 000 |
Пример 3
Корпорация Tristan Inc. имеет банковский кредит, который был взят на следующих условиях:
- сумма кредита $250 000;
- период кредитования 1 год;
- дисконтный процент при номинальной годовой процентной ставке 15%;
- расходы открытие кредитного счета 1% от суммы кредита;
- компенсационный остаток $50 000.
| Проценты к уплате = $250 000 — | $250 000 | = $32 608,70 |
| (1+0,15) 1 |
Дополнительные расходы = $250 000 × 1% = $2 500
Источник