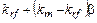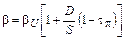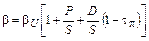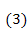Формула р хамады для расчета ожидаемой доходности

Модели Модильяни-Миллера. Формула Хамада

Модель Модильяни — Миллера без учета налогов приводит к выводу о том, что стоимость фирмы не зависит от способа ее финансирования, а также что по мере увеличения доли заемного капитала цена ее акционерного капитала увеличивается.

Модель Модильяни — Миллера с учетом налогов на прибыль. Согласно этой модели рыночная стоимость финансово зависимого предприятия определяется как:

где r — ставка налога на прибыль; D — рыночная оценка заемного капитала; V_U — рыночная стоимость финансово независимого предприятия. Последняя определяется как:

здесь EBIT — прибыль до вычета процентов и налогов; S — общая рыночная стоимость всех обыкновенных акций предприятия; a_sU — цена акционерного капитала финансово независимого предприятия.

Из рассмотренной модели вытекает, что стоимость предприятия увеличивается, а цена его капитала уменьшается по мере роста доли финансирования за счет заемных средств, что не согласуется с практикой и послужило причиной дальнейшего усовершенствования модели.

Р. хамада объединил модель оценки доходности финансовых активов (САРМ) с моделью Модильяни — Миллера с учетом налогов и вывел формулу для определения цены акционерного капитала финансово зависимого предприятия. Эта формула включает три слагаемых:

a_sL = безрисковая доходность + премия за производственный риск + премия за финансовый риск

где a_sL — цена акционерного капитала финансово зависимого предприятия — предприятия, пользующегося заемным капиталом; a_RF — цена акционерного капитала финансово независимого предприятия — предприятия, не пользующегося заемным капиталом; β_U — бета-коэффициент, который предприятие имеет при отсутствии заемного финансирования; r — ставка налога на прибыль; D/S — соотношение рыночных оценок заемного и собственного капитала.

Кроме того, Хамада получил формулу для оценки β-коэффициента финансово зависимого предприятия:

где β_L — рыночный риск предприятия; β_U — производственный риск предприятия; r — ставка налога на прибыль; D/S — уровень финансового левериджа, измеряемого отношением рыночной стоимости заемного капитала — D к рыночной стоимости акционерного капитала — S.

Источник

Модель Хамады

В 1969 году Роберт Хамада скомбинировал модель САРМ и модель ММ с учетом корпоративных налогов. В результате он вывел формулу для расчета стоимости собственно капитала финансово зависимой фирмы, учитывающей как финансовый риск, так и бизнес-риск фирмы:

k_sL = безрисковая ставка + Премия за бизнес-риск + Премия за финансовый риск =

=

β_U — бета-коэффициент фирмы того же класса риска, что и рассматриваемая, но не использующая ЗК.

Эта формула может быть использована для вывода уравнения, с помощью которго можно анализировать влияние финансового рычага на бета-коэффициент:

=

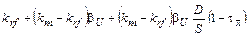
Если бы фирма использовала бы и привилегированные акции:

Р – рыночная стоимость привилегированных акций.

Хамада определил размеры премий к ожидаемой стоимости собственного капитала за риски, отдельно для рыночного и финансового. Рыночный риск – риск, связанный с основной деятельностью предприятия, определяется вероятностью снижения доходности инвестированного капитала. Финансовый риск – риск, связанный с привлечением заемного капитала, определяется вероятностью дефолта должника.

Влияние финансового риска на β-коэффициент определяется через уравнение Хамады:

,

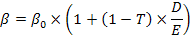
где β₀ – β-коэффициент предприятия, весь капитал которого является собственным, при прочих равных условиях.

В этом случае премия за деловой риск (k_BR) и премия за финансовый риск (k_FR) к стоимости собственного капитала на базе уравнения цены CAPM и уравнения Хамады будут, соответственно, рассчитываться следующим образом:

,

.

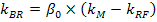
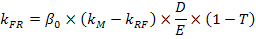
Тогда стоимость собственного капитала будет определяться следующим образом:

(4)

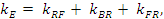
Если привести формулу (4) к уравнению Хамады, получим:

(5)

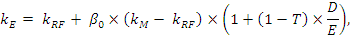
Если в уравнении Хамады k_E заменить на k_S, а балансовый собственный капитал (E) на рыночную стоимость собственного капитала (S), то получится исходный вариант уравнения Хамады, который используется для ожидаемой доходности собственного капитала (в отличии от стоимости собственного капитала). Также существуют различные варианты применения уравнения Хамады в зависимости от видов заемных источников финансирования (например, если таковыми признавать привилегированные акции).

Модель Хамады применяется со всеми допущениями CAPM и модели Модильяни – Миллера, что, естественно, добавляет условность этой модели. На практике модель Хамады используется в основном для оценки изменений в финансовом риске, что, безусловно, важно для принятия решений о структуре капитала. Однако модель Хамады также не разрешает главного противоречия модели Модильяни – Миллера.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Оценка уровня рыночного риска финансово зависимой компании (модель Хамады). Дюрация облигаций

Страницы работы

Содержание работы

1. Модель Хамады: структура капитала и учет рыночного риска.

Cтоимость компании может возрастать с увеличением доли ее капита­ла из заемных источников.

Повышение коэфф. задолженности повышает риск, которому подвергаются акционеры, и это влияет на стоимость акционерного капитала и компании. Оценка уровня рыночного риска финансово зависимой компании (модель Хамады), объедин. ценовую модель рынка капиталов (САРМ) и модель ММ с учетом корпорат. налогообложения.

Формула для расчета стоимости соб­ственного капитала финансово зависимой компании (r_s):

где r— безриск. ставка процента; r_fрыночная дох-ть ин­вест.; b _G — коэфф. b компании той же группы делового риска (деловой риск зависит от удельного веса пост. издержек, которые компания включает в свою операционную деят-ть. =>чем выше пост. издержки компании, тем больше ее деловой риск), что и рассматриваемая, но не имеющая финансового левериджа; (r_f—r) b_G — премия за деловой риск; (r_f –r)b_G (D/S)(1-t) — премия за финансовый риск. Ф-ла Хамады представляет требуемую дох-ть акционерного капитала (S) как сумму трех составляющих: без­рисковой доходности, компенсирующей акционерам временную стоимость их денежных средств, премии за деловой (операционный) риск и премии за фин. риск. Формула САРМ (для оценки требуемой доходности ак­ционерного капитала компании):

r_s =r +(r_f –r)b_G

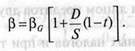
Приравняв правые части этого уравнения и формулы Хамады, по­лучим:

При допущениях, на кот. основаны модели ММ и САРМ, коэфф. акционерного капитала финансово за­висимой компании равен коэфф. b который имела бы эта фирма, если бы она не использовала заемный капитал), откорректи­рованному на ставку корпоративного налога (1 — t) и коэффициенту задолженности компании (D/S).

=>рыночный риск компании, измеряемый коэфф. b, зависит как от делового риска этой комп., мерой ко­торого служит b_G , так и от фин. риска, величина которого оп­р-ся отношением (D/S).

Если облигации имеют одинаковую дох-ть, должна быть рассчитана дюрация для соотв. облигаций.(рис.1)

Дюрация — это пок-ль взвешенного среднего значения сро­ков времени до наступления каждого платежа (купонных и основно­го) по соответствующей облигации.

В качестве весовых коэфф. (W_t) рассматривается приве­денная ст-ть соотв. платежа (PV_t) отнесенная к цене данной облигации:

Пример расчета пок-ля дюрации для облигации(пара­метры: 9 %-ная купонная ставка; срок погашения — 8 лет; дох-ть к погашению — 10 %; номинальная ст-ть— 1000 USD.) Ден. поступления по облигации в первые 7 лет представляют собой купонные платежи по 90 USD, а в по­следний год к купону добавляется выплата номинала облигации; (N— 1000 USD), поэтому совокупный платеж сост. 1090 USD.] Высота каждого столбца на рис. 1 соотв-т величине платежа а их заштрих. часть — привед. стоимости платежа (Р) при ставке дисконт-я 10 %.

Если временная ось — это весовая доска с опорой, то дюрация облигации — это расстояние от начала временной оси до точки опоры, опираясь на которую весы находятся в равнове­сии. Общая формула для расчета дюрации облигации имеет вид:

Для рассматриваемого примера D= 5,97 годам. Рассчит. пок-ль дюрации может быть использован:1.для оценки рыночного риска отдельного фин. инстру­мента: чем выше дюрация инструмента, тем выше его рыночн. риск; 2. для оценки рыночн. риска портфеля различных фин. инструм.

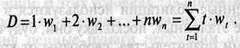
Вывод: 1.дюрация фин. инструм., по кот. не выпл-ся купон с момента выпуска или в течение времени, оставш-ся до погашения, напр.,облигации с нулевым купоном, равна вре­мени, оставшемуся до срока погашения; 2.дюрация обычной облигац. всегда меньше ее срока погаш-я. Напр., облигация с 10-летн. сроком погаш-я, по кот. выплач-ся 10 %-ный купон, имеет приблиз. дюрацию 7 лет; 3. чем выше купонная ставка, тем ниже дюрация, а облигац. ме­нее рискованна, и наоборот;4. дюрация облигации измен-ся со временем — по мере приближ-я срока погашения точка равновесия смещается; 5.чем выше дох-ть облигации, тем ниже дюрация, и наобо­рот. (т.к. при более высокой ставке дох-ти будущие потоки наличности дисконт-ся в больш. степени, чем ближайшие потоки наличн.. Когда же дох-ть облигации падает, точка равновесия смещается вправо.)

Источник

Модель Хамады: структура капитала и учет рыночного риска

Страницы работы

Содержание работы

Вопрос 97. Модель Хамады: структура капитала и учет рыночного риска.

В условиях налогообложения прибыли корпораций способ финансирования, как это показано нами выше, имеет значение, в частности, стоимость компании может возрастать с увеличением доли ее капитала из заемных источников.

Однако повышение коэффициента задолженности повышает также и риск, которому подвергаются акционеры, и это также не может не оказывать влияния на стоимость акционерного капитала, а, следовательно, и компании. Оценка уровня рыночного риска финансово зависимой компании может быть осуществлена с использованием модели Роберта Хамады, объединившего ценовую модель рынка капиталов (CAPM) и модель ММ с учетом корпоративного налогообложения. В результате он вывел следующую формулу для расчета стоимости собственного капитала финансово зависимой компании (r_S):

.

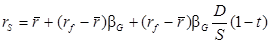
Здесь: 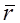– безрисковая ставка процента;

r_f – рыночная доходность инвестиций;

b_G – бета коэффициент компании той же группы делового[1] риска, что и рассматриваемая, но не имеющей финансового левериджа;

– премия за деловой риск;

– премия за финансовый риск.

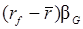
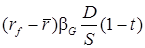
Таким образом, формула Хамады представляет требуемую доходность акционерного капитала (S) как сумму трех составляющих: безрисковой доходности, компенсирующей акционерам временнýю стоимость их денежных средств, премии за деловой (операционный) риск и премии за финансовый риск.

Выше нами было показано, что для оценки требуемой доходности акционерного капитала компании может быть применена формула САРМ:

.

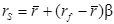
Приравняв правые части этого уравнения и формулы Хамады, получим:

,

.

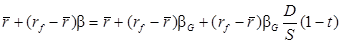
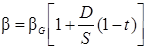
Таким образом, при допущениях, на которых основаны модели ММ и САРМ, бета коэффициент акционерного капитала финансово зависимой компании равен бета коэффициенту, который имела бы эта фирма, если бы она не использовала заемный капитал, откорректированному на ставку корпоративного налога (1 – t) и коэффициент задолженности компании (D/S).

Следовательно, рыночный риск компании, измеряемый коэффициентом b, зависит как от делового риска этой компании, мерой которого служит b_G, так и от финансового риска, величина которого определяется отношением (D/S).

[1] Деловой риск в значительной степени зависит от удельного веса постоянных издержек, которые компания включает в свою операционную деятельность. Таким образом, при прочих равных условиях, чем выше постоянные издержки компании, тем больше ее деловой риск.

Источник