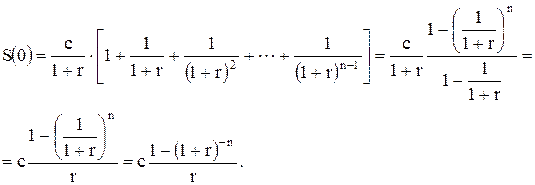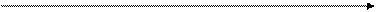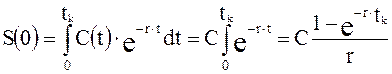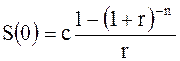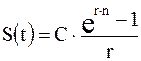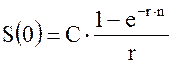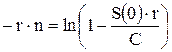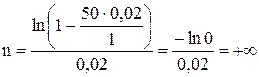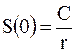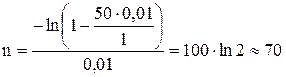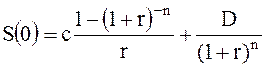Финансовая рента как инвестиция

Аннуитет и финансовая рента в инвестициях

В большинстве коммерческих операций вместо разовых платежей встречается последовательность денежных поступлений или выплат. Серия потоков поступлений или выплат называется потоком платежей . Поток однонаправленных платежей с равными интервалами времени между последовательными платежами в течение определенного количества лет представляет собой аннуитет (финансовая рента) .

Денежные поступления при оценке долговых и долевых ценных бумаг, возможных арендных платежей можно представить следующим образом:

Аннуитеты могут подразделяться по количеству выплат в году, т. е. годовые выплаты (1 раз в год) и срочные (ряд выплат в пределах года), а также по количеству начислений процентов в течение года (ежегодно несколько раз в год или непрерывно).

По времени наступления платежей различают два типа аннуитета:

1. Обыкновенный (постнумерандо) аннуитет — когда платежи происходят в конце каждого периода.

2. Авансовый (пренумерандо) аннуитет — когда платежи происходят в начале каждого периода.

По продолжительности денежного потока различают:

3. Срочный аннуитет — денежный поток с равными поступлениями в течение ограниченного промежутка времени.

Примером срочного аннуитета постнумерандо являются арендные платежи, за пользование имуществом, землей и т. п., которые регулярно поступают по истечении очередного периода. В качестве примера срочного аннуитета пренумерандо можно представить схему периодических денежных вкладов на банковский счет в начале каждого месяца с целью наполнения определенной суммы, необходимой для решения конкретной задачи.

1. Бессрочный аннуитет — когда денежные поступления продолжаются достаточно длительное время.

Будущая стоимость обыкновенного аннуитета

Будущая стоимость обыкновенного аннуитета рассчитывается по следующей формуле:

где — денежные поступления аннуитета; — коэффициент наращения будущей стоимости аннуитета.

Для денежного потока из периода будущая стоимость авансового аннуитета равна:

Для определения суммы, которую необходимо депонировать в конце каждого периода для того, чтобы через заданное число периодов остаток составил необходимую величину, используется функция, называемая фактор фонда возмещения :

Данный фактор учитывает процент, получаемый по депозитам. Сумма ежегодного вклада составит:

где — стоимость поступлений по истечении срока вложений.

Формула (1.17) применяется для определения суммы, которую следует ежегодно вкладывать на депозитный счет в банк, чтобы через определенное количество лет получить заданную стоимость.

Часто в тех случаях, когда вплоть до истечения срока кредитного договора (долгового обязательства) кредитору выплачивается только процент, заемщики для погашения основной суммы кредита создают специальные фонды возмещения. В каждый период должник вносит в отдельный фонд сумму, которая вместе с начисляемым на нее процентом должна обеспечить погашение основной части кредита.

Пример 3. Чтобы получить 800 тыс. руб. в конце четырехлетнего периода при нулевом проценте, необходимо депонировать тыс. руб. Если процентная ставка составит 10 %, тогда можно депонировать

Разница четырех взносов (524,2 тыс. руб.) и полученной суммы составит 275,8 тыс. руб.

Настоящая и текущая стоимость обыкновенного аннуитета

Настоящая стоимость обыкновенного аннуитета для денежного потока из периодов рассчитывается по формуле:

Отдельные элементы денежного потока относятся к разным временным интервалам, поэтому их суммирование искажает реальную доходность инвестиций. Приведение денежного потока к одному моменту времени осуществляется при помощи функции, называемой текущей стоимостью аннуитета.

Текущая стоимость обыкновенного аннуитета определяется по формуле:

где — коэффициент дисконтирования настоящей стоимости аннуитета.

Пример 4. В результате осуществления инвестиционного проекта ежегодные доходы в течение 5 лет будут составлять по 500 тыс. руб.

Текущая стоимость денежных потоков составит:

В результате дисконтирования дохода за каждый период получим:

В тех случаях, когда денежные поступления приходят в начале периода, настоящая стоимость авансового аннуитета для денежного потока из периодов рассчитывают следующим образом:

Формула (1.20) применяется для определения текущей стоимости, если доходы, получаемые за каждый i-й период, равны. При неравенстве доходов по временным периодам их получения рассчитывается дисконтированная стоимость за каждый период.

Функция погашения кредита

Для определения дохода, который необходимо получать ежегодно, чтобы возместить (окупить) инвестиции за определенный период времени с учетом процентной ставки, используется функция погашения кредита :

Формула (1.21) применяется для определения суммы, которую необходимо ежегодно (ежеквартально) вносить в банк для погашения кредита и процентов по нему.

Ежегодный доход (аннуитет) определяется умножением суммы инвестиций на множитель

где — начальная сумма инвестиции (вложений).

Пример 5. Инвестиции в проект составили 900 тыс. руб. Чтобы окупить инвестиции в течение 5 лет и получить доход в размере 10 % годовых, ежегодный денежный поток (аннуитет) должен составить:

Настоящая стоимость бессрочного аннуитета

Настоящая стоимость бессрочного аннуитета определяется по формуле:

Бессрочным называется такой денежный поток, при котором денежные поступления продолжаются весьма длительное время (например, аренда на 50 лет и более).

Формула (1.23) показывает максимальную цену, которую инвестор согласен заплатить за бессрочные денежные поступления. Для этого в числителе используют размер годовых поступлений, а в знаменателе в качестве коэффициента дисконтирования обычно принимается гарантированная процентная ставка (например, процент по государственным ценным бумагам).

Источник

Финансовая рента (аннуитет)

Важным частным случаем потока платежей является финансовая рента или просто рента (rent), называемая иногда также аннуитетом (annuity).

Под финансовой рентой понимается поток платежей, у которого все выплаты одного знака и производятся через равные промежутки времени.

Примером рент являются: квартирная плата, погашение кредита, пенсии, регулярные выплаты процентов, ипотека, страховые выплаты и т. д. Первоначально рассматривались лишь ежегодные выплаты (anno-год) отсюда название аннуитет (annuity).

Интервал времени между выплатами называется периодом ренты (rent period, payment period); размер отдельного платежа – членом ренты (rent). Сроком ренты (temp) называется время от начала первого периода ренты до конца последнего периода.

Если выплаты производятся в конце периода, то рента называется рента постнумерандо или обыкновенная рента (аннуитет постнумерандо или обыкновенный аннуитет, ordinary annuity).

Если выплаты производятся в начале периода, то рента называется рента пренумерандо или авансированная рента (аннуитет пренумерандо или авансированный аннуитет, annuity due). Иногда выплаты ренты производятся в середине периода, например пенсии.

Для безусловной ренты (annuity certain) заранее оговариваются моменты всех выплат – от первой до последней выплаты. Для условной ренты (contingent annuity) даты первой и последней выплаты зависят от какого-либо случайного события. Примером такой ренты являются страховые выплаты или пенсии (life annuity). Для описания и оценки условных рент создана бурно развивающаяся в настоящее время страховая (актуарная) математика.

Существуют и бессрочные (вечные) ренты. Пример такой ренты это облигации Британского казначейства (Х1Х век), выплаты по ним производятся два раза в год по 2,5 % годовых.

Простая рента означает выплаты одной суммы, сложная рента предполагает выплаты переменных сумм.

Проведем расчет простой ренты постнумерандо (см. рис. 3.4).

Если член ренты – с, а процентная ставка – r, то современная стоимость ренты будет равна:

(3.4)

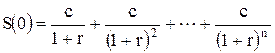
Суммируя геометрическую прогрессию, по формуле 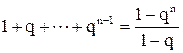получим:

Окончательно . (3.5)

или .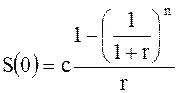

Наращенная сумма S(n) согласно (3.2) будет равна:

. (3.6)

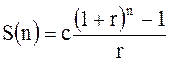
Расчет простой ренты пренумеранто сводится к следующему потоку платежей (см. рис. 3.5).

Современная стоимость ренты равна:

.

Суммируя геометрическую прогрессию аналогично предыдущему, получим:

. (3.7)

Для наращенной суммы получим:

. (3.8)

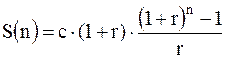
Сравнивая (3.7) и (3.8) с (3.5) и (3.6), убеждаемся, что рента пренумерандо дороже ренты постнумерандо. Точнее справедлива формула:

, (3.9)

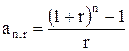
называемой коэффициентом наращивания, существуют специальные таблицы. Однако в настоящее время его вычисление не составляет труда. Используя коэффициент наращивания, формулы (3.5) и (3.8) запишутся:

постнумерандо	пренумерандо
S(0)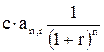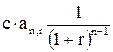
S(n)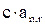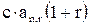

Непрерывная рента.

Если выплаты ренты производятся достаточно часто и длительный промежуток времени, удобно от дискретной ренты перейти к непрерывной ренте. Рассмотрим соответствующий непрерывный поток платежей. Произведем расчет современного значения PV = S(0) и будущего значения FV = S(t_k) для данного потока платежей.

ПустьC(t) dt – значение платежа в момент времени t за промежуток времени dt, срок ренты равен t_k,начало ренты в момент 0 конец в момент t_k. В общем случае предполагается возможность выплаты переменных сумм C(t).

S(0)=PV C(t)dt S( )=FV

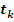
0 t

Для оценки непрерывного потока платежей рассчитаем современное значение или приведенную к начальному моменту денежную сумму S(0) = PV.Предположим, что процентная ставка равна r. Тогда, платеж C(t) dtв пересчете на начальный момент должен дисконтироваться, то есть умножаться на число меньше единицы равное e — r t (см. формулу (2.12) для непрерывных процентов) и дисконтированный платеж будет равен e — r t C (t) dt. При этом приращение современного значения S(0) будет равно:

(3.10)

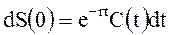
После интегрирования дифференциального уравнения по всему сроку рентыотначала ренты в момент 0 до конца ренты в моментt_kполучим дляоценкисовременного значения непрерывной ренты следующий интеграл:

(3.11)

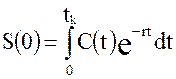
Формула применима для оценки сложной ренты, когда предполагаются выплаты переменных сумм C (t).

Простая непрерывная рента: Если рента предполагает выплату постоянно одной и той же суммы С, то рента называется простой. Произведем расчет современного значения PV = S(0) и будущего значения FV = S(t_k) для данного потока платежей. В этом случае имеем C(t) = C и соответствующий интеграл может быть легко вычислен:

Окончательно для современного значения получаем:

(3.12)

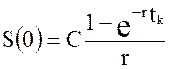
Учитывая, что длительность сделки равна t_k , а процентная ставка равна r, будущее значение S(t_k) по формуле непрерывных процентов (2.12) будет равно:

Отсюда окончательно получим для простой непрерывной ренты будущее значение:

(3.13)

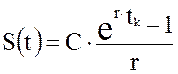
Иногда момент окончания сделки удобно принять за t_k = n тогда выведенные выше формулы будут иметь чуть более компактный вид. Для непрерывной ренты имеем современное значение:

. (3.14)

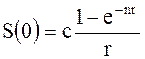
Формула для бессрочной (вечной ренты) получается из (3.5) или (3.14) предельным переходом при и имеет вид:

(3.15)

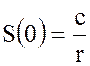
Для непрерывной ренты наращенная сумма будет равна:

. (3.16)

Рассмотрим примеры использования полученных формул.
Пример 32.

Кредит 5 млн руб. погашается 12 равными ежемесячными взносами. Найти сумму выплат при ставке 12 % годовых.

Воспользуемся формулой (3.4):

,

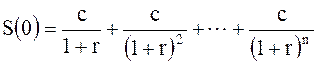
где S(0)=5 млн руб.; число периодов начисления n=12, r=1%=0,01 – годовая ставка, пересчитанная на 1 месяц, т. е. .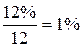

Тогда, согласно (3.5) имеем:

,

(3.17)

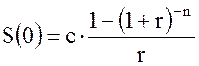
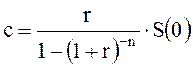
Подставляя числа, получим:

млн руб.

Для приобретения недвижимости стоимостью 60 тыс. $ берется кредит под 6 % годовых. Согласно контракту погашение кредита происходит каждый месяц в течение 30 лет. Какова сумма месячного платежа?

Длительность ренты в месяцах равна 360. Воспользуемся формулой (3.4) для установления связи между неизвестным членом ренты с, современной стоимостью ренты S(0)=60 тыс. $ и месячной процентной ставкой .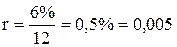

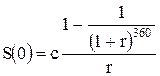
, тогда, суммируя, получим из (3.5):

.

Отсюда, сумма месячного платежа равна:

тыс. $ = 359,73 $.

Если воспользоваться формулами для непрерывной ренты (3.10), получим:

тыс. $=359,41 $.

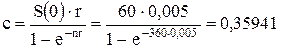
Очевидно, что суммы ежемесячного платежа, рассчитанные по непрерывным и дискретным формулам, близки.

Кредит погашается в течение года ежемесячными платежами в размере 2 тыс. руб., годовая процентная ставка составляет 12 %. Необходимо найти величину кредита.

Воспользуемся сначала формулой (3.5) вычисления современного значения обыкновенной дискретной ренты:

В нашей задаче член ренты равен c = 2 тыс. руб., срок ренты n = 12 месяцев, месячная процентная ставка равна r = 12 %/12 = 1 % (1/мес.), а неизвестной является величина кредита S(0). Тогда:

тыс. руб.

В непрерывном случае для решения воспользуемся формулой:

,

= 22,616 тыс. руб.

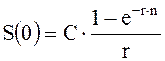
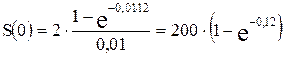
Сумма кредита составляет 22616 руб. ‑ она чуть больше суммы 22510 руб., рассчитанной по дискретной формуле.

Планируется покупка автомобиля FORD F650 стоимостью $250 тыс. через 5 лет. Необходимо найти сумму, которую будем откладывать ежемесячно в течение указанного срока под годовую процентную ставку 6 % для осуществления запланированной покупки.

Воспользуемся сначала формулой (3.6) вычисления будущего значения обыкновенной дискретной ренты:

В нашей задаче член ренты c неизвестен, а известны: срок ренты n=5*12=60 месяцев, месячная процентная ставка равна r=6%/12=0,5%=0,005 (1/мес.), и будущее значение S(n)=$250 тыс.

тыс.

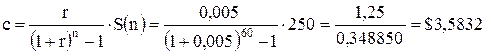
В непрерывном случае для решения воспользуемся формулой (3.15):

тыс.

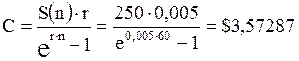
Ежемесячно необходимо откладывать суммы в размере $ 3572,87 ‑ при расчете по непрерывным процентам или $ 3583,2 ‑ при расчете по дискретным процентам.

В момент рождения ребенка родители начинают откладывать ежемесячно $C на его обучение в университете. Плата за весь срок обучения составляет $100 тыс. и вносится в момент поступления ребенка в университет. Ребенок поступает в университет в возрасте 17 лет. Банковская ставка составляет 6 % в год. Найти величину $C.

Задача решается аналогично предыдущему примеру 35. Известны: срок ренты: n=17*12=204 месяцев, месячная процентная ставка равна r=6%/12=0,5%=0,005 (1/мес.), и будущее значение S(n)=$100 тыс. Нужно найти месячный платеж (член ренты) с:

тыс.=$283,1.

тыс.=$281,98

На обучение ребенка в университете нужно откладывать ежемесячно $283,1 при дискретном расчете или =$281,98 при непрерывном расчете.

В конце каждого месяца на сберегательный счет инвестируется 2 тыс. руб. На поступающие платежи ежемесячно начисляются сложные проценты по годовой ставке 12 %. Какова величина вклада через 2 года? Какую сумму нужно разместить инвестору на депозитный счет для получения такой же величины вклада через 2 года в предположение, что проценты начисляются по той схеме – ежемесячно?

Из условия примера член ренты C=2 тыс. руб., длительность ренты n=24 (мес.), месячная процентная ставка r =12%/12=1%=0,01 (1/мес.).

Сначала, для определения величина вклада через 2 года воспользуемся формулой (3.6) вычисления будущего значения обыкновенной дискретной ренты

тыс. руб.

Затем, для определения суммы, которую нужно разместить инвестору на депозитный счет, воспользуемся формулой (3.5) вычисления современного значения обыкновенной дискретной ренты:

тыс. руб.

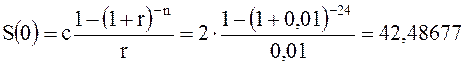
Таким образом, размещение суммы 42,48677 тыс. руб. на депозитный счет для начисления ежемесячно сложных процентов по годовой ставке 12 % позволит инвестору получить ту же сумму вклада 53,9493 тыс. руб.

Банк N дает кредит под 24 % годовых. Один из вариантов кредитного договора имеет следующий вид:

«Кредит на 50 тыс. руб. погашается ежемесячными платежами в размере 2 тыс. руб. Половина суммы идет на обслуживание кредита, другая половина – на погашение кредита. Банк N дополнительно сообщает клиенту о моменте погашения кредита».

Таким образом, ежемесячно в счет погашения заемщик платит 1 тыс. руб.

Сколько должно быть выплат, чтобы погасить кредит? Каков срок погашения кредита, если процентная ставка будет снижена до 12 % или повышена до 28 % годовых?

В нашей задаче член ренты равен c = 1 тыс. руб., месячная процентная ставка равна r = 24%/12 = 2 % = 0,02 (1/мес.), величина кредита S(0)=50 тыс. руб., а неизвестным является срок ренты n.

Воспользуемся формулой (3.14) вычисления современного значения непрерывной ренты:

Отсюда найдем количество выплат n

(3.18).

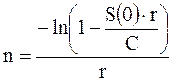
В нашем случае имеем S(0) = 50 тыс.руб.; C = 1 тыс. руб.; r=0,02. Подставив исходные данные в полученную формулу, вычислим количество выплат n

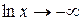
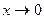
Так как, при и, следовательно, n →+∞.

Таким образом, срок погашения кредита равен +∞, то есть клиент, заключивший договор с банком N, будет должен ему вечно.

Возможно, в рассуждениях и расчетах имеется ошибка, рассмотрим задачу с другой стороны. Если сумма выплат С постоянна, а количество выплат n стремится к бесконечности, то для современного значения PV=S(0) такого потока платежей получим формулу (3.15):

В рассматриваемом случае, если клиент банка будет платить по тысяче рублей ежемесячно под r=2 % в месяц вечно, то он погасит кредит. Действительно

= 50 тыс. руб.

Пусть теперь процентная ставка снижена до 12 %. Рассчитаем количество выплат n при этом значения процентной ставки r=12 %/12=1 %=0,01

Таким образом, для погашения кредита в 50 тыс. руб. на условиях предложенных банком N при небольшом проценте 12 % годовых потребуется 70 выплат по 2 тыс. руб. т. е. 140 тыс. руб. в течение 70/12=5,8333 лет.

Если процентная ставка будет повышена до 28 % , то современное значение PV=S(0) при r=28 %/12=2,333% и C=1 тыс. руб. для бесконечного потока платежей равно:

= 42,86 тыс. руб.

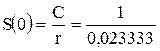
Полученная величина меньше суммы кредита в 50 тыс. руб., то есть, при годовой ставке в 28 %, даже выплачивая вечно, не удастся погасить сумму кредита. Потомки неосторожного клиента банка N будут перед ним в вечном долгу.

Для полноты приведем решение данного примера с использованием формулы дискретной ренты:

Отсюда число периодов начисления равно:

(3.19)

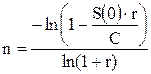
Формулы (3.18) и (3.19) отличаются только знаменателем, но при малых значениях процентной ставки r согласно замечательному пределу ln (1+r) примерно равен r и знаменатели практически совпадают и, следовательно, все полученные выше результаты остаются в силе.

Ссуда в 10 млн руб. выдана под 12 % годовых (т. е. 1 % месячных) и требует ежемесячной оплаты по 130 тыс. руб. и выплаты остатка долга к концу срока в 10 лет. Каков остаток долга D?

В задаче месячная ставка равна r=1 % (1/мес.), число выплат n=10*12=120 (мес.), ежемесячные выплаты c=130 тыс. руб.=0,13 млн руб., ссуда равна S(0)=10 млн руб. Неизвестным является остаток долга D.

Поток платежей для данной задачи имеет вид:

Следовательно, приведенный доход S(0)=PV равен:

Отсюда, остаток долга:

Подставляя численные значения, получим:

млн руб.

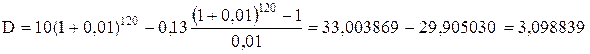
Следовательно, долг равен D=3,098839 млн руб.

Владелец оливковой рощи сдал её в «вечную» аренду. Арендатор, начиная с 2010 года, переводит 1 января каждого года на банковский счет владельца оливковой рощи арендный платеж в размере $40 тыс. Банк ежегодно начисляет на вклад сложные проценты, исходя из годовой процентной ставки 5 %. Какова выкупная цена оливковой рощи на 1 января 2010 года? Найти выкупную цену оливковой рощи на 1 января 2015 года.

Ответы и указания:

Выкупная цена оливковой рощи на 1 января 2010 года определяется по формуле вечной ренты пренумерандо:

тыс.

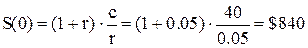
Выкупная цена оливковой рощи на 1 января 2015 года равна:

$1072,077 тыс.

Источник