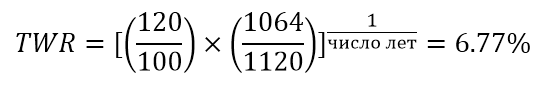Доходность взвешенная по времени twr

Реальная доходность портфеля: расчет и смысл

Некоторое время назад я писал статью о расчете рыночной доходности. Статья несомненно важная и рекомендуется всем, кто имеет дело с инвестициями, поскольку очень многие считают доходность либо неправильно (обычно новички, в частности путая среднеарифметические и среднегеометрические данные), либо намеренно завышают результат (обычно инвестиционные фонды, экстраполируя удачные квартальные показатели в будущее).

Тем не менее у приведенных расчетов есть недостаток. Дело в том, что разовое инвестирование одной суммы (без промежуточных вводов и выводов до выхода из рынка) это скорее гипотетический подход. Даже если не брать во внимание купонные выплаты и дивиденды, которые не всегда могут быть сразу же реинвестированы, реальное инвестирование предполагает периодические вводы и выводы средств, что плохо вписывается в представленные по ссылке формулы.

Два вида доходности: TWR и MWR

Представим такую ситуацию. Мы инвестировали в рынок 100 долларов, которые за год выросли на 20%. Соответственно, у нас на счету оказалось $120. Довольные результатом, мы вносим теперь 1000 долларов. Однако рынок ведет себя иначе: на следующий год он падает на 5%. Следовательно, наша конечная сумма оказывается равна 1120 × (1 – 0.05) = $1064. А как подсчитать полученную доходность?

В этом случае есть два способа:

• TWR (Time Weighted Return / доходность, взвешенная по времени)
• MWR (Money Weighted Retutn / доходность, взвешенная по деньгам)

Разберемся с ними отдельно.

1. TWR

Считается более традиционной, хотя это можно оспорить. Для ее расчета инвестиционный процесс разбивается на интервалы, в которых происходят ввод или вывод средств, таким образом нивелируя их влияние на результат. В нашем случае инвестиции разбиты на два равных годовых отрезка (число лет =2):

Фактически TWR отражает доходность неизменной суммы инвестора с начала инвестиций без пополнений и снятий. Но насколько логичен этот результат у нас? На первом отрезке мы заработали $20, однако на втором потеряли 1064 – 1120 = $56. Т.е. фактически у нас убыток, вызванный многократным увеличением вклада при последующем снижении рынка, а TWR считает нам плюс, игнорируя абсолютное значение взноса.

2. MWR

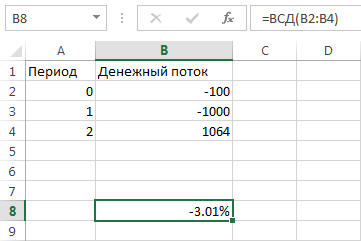
Учесть этот недостаток TWR может доходность, взвешенная по деньгам. Она отражает движение денежных средств и может быть посчитана при помощи функции ВСД в Excel. Для этого нам нужны вносимые средства со знаком «минус» и конечный результат на счете. Для случая выше расчет следующий:

Итого, MWR = – √1 + (3.01%/100%) = –1.49%. Корень означает степень ½, где 2 — число лет инвестиций. Как видно, доходность по деньгам более адекватно описывает поведение нашего реального счета, хотя для ее вычисления мы прописываем только ввод средств и конечный результат. MWR и TWR встречаются в аналитике зарубежных брокеров и в сервисах расчета инвестиционных портфелей.

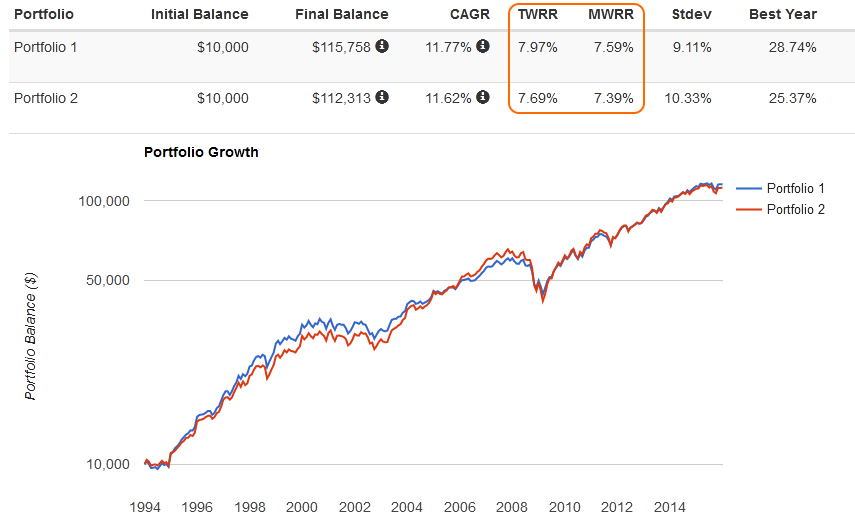
CAGR (Compound Annual Growth Rate) в данном случае включает в результат все вносимые инвестором средства (ежегодно $1000), не отделяя их от рыночной доходности – поэтому результат получается заметно лучше.

Итоги

Наша ситуация вполне могла быть обратной: вначале мы получаем заметный минус на малую сумму, затем вносим гораздо больше и фиксируем небольшой плюс. Нетрудно рассчитать, что тогда TWR будет отрицательной, а MWR положительной. Можно сказать, что TWR описывает стратегию инвестора в целом, тогда как MWR включает в нее движения средств — таким образом, удачно влив крупную сумму перед периодом роста можно заметно улучшить доходность стратегии. И наоборот.

Учет инвестиций с помощью ЧИСТВНДОХ

Проблема функции ВСД в том, что она верна для периодических денежных потоков, поступающих и/или убывающих через равные промежутки времени. Однако понятно, что в реальных инвестициях ввод/вывод средств обычно происходит в спонтанном режиме. В этом случае для расчета доходности портфеля можно воспользоваться функцией ЧИСТВНДОХ.

Вся подобная статистика должна содержаться в брокерском отчете. Вычисления выполняются с помощью итерационного метода, подробное описание функции можно найти здесь .

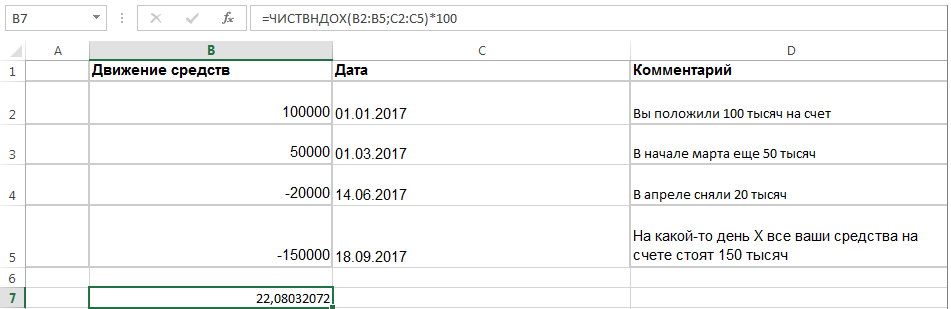
Основными в расчете являются две колонки: значений (введенных и выведенных средств) и соответствующих дат, когда происходил ввод или вывод денег. Обратите внимание, что общая стоимость активов указывается со знаком минус. После чего в произвольную ячейку, где требуется результат, нужно ставить следующую формулу:

В2:B5 — диапазон ячеек со значениями введенных или выведенных средств

С2:С5 — диапазон ячеек с датами, когда происходил ввод или вывод

Умножение на 100 позволяет получить результат в процентах. Для примера выше средняя годовая доходность будет ≈ 22.1%.

🔔 При инвестициях меньше года подобный расчет является некорректным. Кроме того, поскольку на рынке периодически возникают пузыри (доткомов на рынке США в 1995-2000 годах или российских активов на росте нефти в 2000-2008), а также бывают затяжные кризисы (обычно именно после пузырей — например Великая Депрессия 30-х или Япония после 1990 года), то для более адекватной оценки портфеля гораздо лучше подходят временные интервалы в несколько лет, чем за 1-2 года.

В заключении пример доходности инвестиционного портфеля одного моего клиента:

Источник

Результаты управления: Измерение доходности — 2

В продолжение предыдущего поста.

Доходность, взвешенная по времени.

Отражает рост каждого рубля на счету. Для этого нужно, соответственно, знать точно дату, когда пришел этот «каждый рубль», т.е. необходимо пересчитывать стоимость портфеля при каждом внесении (выводе). Довольно трудоемко, но зато точно. В связи с этим Глобальные стандарты оценки результатов инвестирования предпочитают именно этот расчет.

Сама формула выглядит так 1 + r_t = [(1 + r_t,1) * (1 + r_t,2) * … * (1 + r_t,n)] 1/ n , где r_t и есть доходность нашего портфеля, а r_t,n представляет собой доходность за периоды между внесением (выводом) средств.

Пример. На начало месяца у меня 2,500,000 рублей на счете, в конце 2,700,000. 7-го числа я внес 45,000 рублей и 19-го — 25,000, при этом стоимость портфеля на эти даты 2,555,000 и 2,575,000 соответственно:

r_t,1= ((2,555,000 − 45,000) − 2,500,000) / 2,500,000 = 0.4%

Второй субпериод (8−19).
r_t,2 = ((2,575,000 − 25,000) − 2,555,000) / 2,555,000 = −0.2%

Третий (20−30 дней).
r_t,3 = (2,700,000 − 2,575,000) / 2,575,000 = 4.9%

Итого получаем, склеив все субпериоды, r_t = (1 + 0.004) * (1 − 0.002) * (1 + 0.049) – 1 = 5.1% за месяц из 30 дней.

Доходность, взвешенная по деньгам. Здесь ситуация несколько сложнее, т.к. потребуется расчет внутренней нормы доходности (IRR) либо на калькуляторе, либо в экселе. Зато менее затратная в плане отсутствия необходимости высматривать все входящие и исходящие средства клиентов, но и менее точная поэтому.

Например. На начало месяца у меня 900,000 на счете, 15-го числа я вношу еще 50,000. И в конце месяца у меня 1,466,553. Считаем так: 1,466,553 = 900,000 * (1 + IRR) 2 + 50,000 * (1 + IRR), отсюда IRR = 24.9% за 15 дней (!), что составляет (1.24904 2 – 1) = 56.01% в месяц.

Сравнение обоих методов.

Клиент инвестировал 100,000 в начале года, на конец года стоимость активов возросла до 105,000. Доходность по обоим методам составить 5%. Клиент вносит еще 95,000, т.е. общая стоимость портфеля на начало втророго года получается 200,000 и увеличивается к концу до 220,000. Доходность по второму году уже 10%. Сколько за 2 года?

Взвешенная по времени r_t = (1.05 * 1.10) 1/2 – 1 = 7.47% в год или 15.50% за два.

Взвешенная по деньгам 100,000 * (1 + r_t) 2 + 95,000 * (1 + r_t) 1 = 220,000 и r_t = 8.24% или (1.0824 2 – 1) = 17.16% за два.

Я, кстати, планирую опустить требования к бенчмарку, против которого надо оценивать доходность портфеля. Если надо, конечно, могу и написать 🙂 Получается, что в следующем посте будет определять источник нашей доходности.

Источник

Доходность, взвешенная по времени — Time-weighted return

Взвешенной по времени возврата (TWR) представляет собой метод расчета возврата инвестиций. Чтобы применить метод взвешенной по времени доходности, объедините доходность за подпериоды, сложив их вместе, в результате чего получится общая доходность за период. Норма прибыли для каждого отдельного подпериода взвешивается в соответствии с продолжительностью подпериода.

Метод, взвешенный по времени, отличается от других методов расчета доходности инвестиций только тем, как он компенсирует внешние потоки — см. Ниже.

СОДЕРЖАНИЕ

Внешние потоки

Доходность, взвешенная по времени, является мерой исторической эффективности инвестиционного портфеля, которая компенсирует внешние потоки . Внешние потоки — это чистые движения стоимости, которые возникают в результате переводов денежных средств, ценных бумаг или других инструментов в портфель или из него, без одновременного равного и противоположного движения стоимости в противоположном направлении, как в случае покупки или продажи, и которые не являются доходом от инвестиций в портфель, например проценты, купоны или дивиденды.

Чтобы компенсировать внешние потоки, общий анализируемый временной интервал делится на непрерывные подпериоды в каждый момент времени в пределах общего временного периода всякий раз, когда есть внешний поток. Как правило, эти подпериоды будут неравной продолжительности. Доходность за подпериоды между внешними потоками геометрически связаны (составлены) вместе, то есть путем умножения вместе факторов роста во всех подпериодах. (Фактор роста в каждом подпериоде равен 1 плюс доходность за подпериод.)

Проблема внешних потоков

Чтобы проиллюстрировать проблему внешних потоков, рассмотрим следующий пример.

Пример 1

Предположим, инвестор переводит 500 долларов в портфель в начале первого года и еще 1000 долларов в начале второго года, а общая стоимость портфеля составляет 1500 долларов в конце второго года. Чистая прибыль за два года период равен нулю, поэтому интуитивно мы можем ожидать, что доходность за весь двухлетний период составит 0% (что, кстати, является результатом применения одного из методов, взвешенных по деньгам). Если игнорировать денежный поток в 1000 долларов в начале 2-го года, то простой метод расчета доходности без компенсации потока будет составлять 200% (1000 долларов, разделенные на 500 долларов). Интуитивно 200% неверно.

Однако если мы добавим дополнительную информацию, вырисовывается иная картина. Если первоначальные инвестиции выросли в стоимости на 100% в течение первого года, но затем портфель снизился на 25% в течение второго года, мы ожидаем, что общий доход за двухлетний период будет результатом сложения 100% прироста ( 500 долларов) с потерей 25% (также 500 долларов). Взвешенная по времени доходность определяется путем умножения факторов роста для каждого года, то есть факторов роста до и после второго переноса в портфель, затем вычитания единицы и выражения результата в процентах:

( 1 + 1.0 ) ( 1 — 0,25 ) — 1 знак равно 2.0 × 0,75 — 1 знак равно 1.5 — 1 знак равно 0,5 знак равно 50 % <\ displaystyle (1 + 1.0) (1-0.25) -1 = 2.0 \ times 0.75-1 = 1.5-1 = 0.5 = 50 \%> .

Из взвешенной по времени доходности видно, что отсутствие какой-либо чистой прибыли за двухлетний период было связано с неудачным моментом поступления денежных средств в начале второго года.

В этом примере взвешенная по времени доходность является завышенной для инвестора, поскольку он не видит чистой прибыли. Однако, отражая результаты за каждый год, сложенные вместе на уравновешенной основе, взвешенная по времени прибыль признает результативность инвестиционной деятельности независимо от плохого времени движения денежных средств в начале года 2. Если бы все деньги были вложены в начале первого года доходность по любым меркам, скорее всего, составила бы 50%. 1500 долларов выросли бы на 100% до 3000 долларов в конце первого года, а затем снизились бы на 25% до 2250 долларов в конце второго года, что привело бы к общей прибыли в 750 долларов, то есть 50% от 1500 долларов. Разница заключается в перспективе.

Поправка на потоки

Доходность портфеля при отсутствии потоков составляет:

р знак равно M 2 — M 1 M 1 <\ displaystyle R = <\ frac -M_ <1>> >>>

где — окончательная стоимость портфеля, — начальная стоимость портфеля и — доходность портфеля за период. M 2 <\ displaystyle M_ <2>> M 1 <\ displaystyle M_ <1>> р <\ displaystyle R>

1 + р знак равно M 2 M 1 <\ displaystyle 1 + R = <\ frac > >>>

Внешние потоки за анализируемый период усложняют расчет производительности. Если внешние потоки не принимаются во внимание, измерение эффективности искажается: поток в портфель приведет к тому, что этот метод будет завышать истинную производительность, в то время как потоки из портфеля могут привести к занижению истинной производительности.

Чтобы компенсировать внешний поток в портфель в начале периода, скорректируйте начальную стоимость портфеля, добавив . Возврат: C 1 <\ displaystyle C_ <1>> M 1 <\ displaystyle M_ <1>> C 1 <\ displaystyle C_ <1>>

р знак равно M 2 — ( M 1 + C 1 ) M 1 + C 1 <\ displaystyle R = <\ frac — (M_ <1>+ C_ <1>)> + C_ <1>>>>

и соответствующий коэффициент роста:

1 + р знак равно M 2 M 1 + C 1 <\ displaystyle 1 + R = <\ frac > + C_ <1>>>>

Чтобы компенсировать внешний поток в портфель непосредственно перед оценкой в конце периода, скорректируйте окончательную стоимость портфеля путем вычитания . Возврат: C 2 <\ displaystyle C_ <2>> M 2 <\ displaystyle M_ <2>> M 2 <\ displaystyle M_ <2>> C 2 <\ displaystyle C_ <2>>

р знак равно ( M 2 — C 2 ) — M 1 M 1 <\ displaystyle R = <\ frac <(M_ <2>-C_ <2>) — M_ <1>> >>>

и соответствующий коэффициент роста:

1 + р знак равно M 2 — C 2 M 1 <\ displaystyle 1 + R = <\ frac -C_ <2>> >>>

Возврат, взвешенный по времени, с компенсацией внешних потоков

Предположим, что портфель оценивается сразу после каждого внешнего потока. Стоимость портфеля в конце каждого подпериода корректируется с учетом внешнего потока, который имеет место непосредственно перед ним. Внешние потоки в портфель считаются положительными, а потоки из портфеля — отрицательными.

1 + р знак равно M 1 — C 1 M 0 × M 2 — C 2 M 1 × M 3 — C 3 M 2 × ⋯ × M п — 1 — C п — 1 M п — 2 × M п — C п M п — 1 <\ displaystyle 1 + R = <\ frac -C_ <1>> >> \ times <\ frac -C_ <2>> > > \ times <\ frac -C_ <3>> >> \ times \ cdots \ times <\ frac -C_ > >> \ times <\ frac -C_ > >>>

Если в конце общего периода происходит внешний поток, то количество подпериодов совпадает с количеством потоков. Однако, если в конце общего периода нет потока, то он равен нулю, а количество подпериодов на единицу больше, чем количество потоков. п <\ displaystyle n> C п <\ displaystyle C_ > п <\ displaystyle n>

Если портфель оценивается непосредственно перед каждым потоком, а не сразу после него, то каждый поток следует использовать для корректировки начального значения в каждом подпериоде, а не конечного значения, что приводит к другой формуле:

1 + р знак равно M 1 M 0 + C 0 × M 2 M 1 + C 1 × M 3 M 2 + C 2 × . . . × M п — 1 M п — 2 + C п — 2 × M п M п — 1 + C п — 1 <\ displaystyle 1 + R = <\ frac > + C_ <0>>> \ times <\ frac > + C_ <1>> > \ times <\ frac > + C_ <2>>> \ times . \ times <\ frac > + C_ >> \ times <\ frac > + C_ >>>

Объяснение

Почему это называется «взвешенным по времени»

Термин « взвешенная по времени» лучше всего иллюстрируется непрерывной (логарифмической) нормой прибыли . Общая норма доходности — это средневзвешенная по времени непрерывная норма доходности в каждом подпериоде.

При отсутствии потоков,

Конечное значение знак равно начальное значение × е р л о грамм т <\ displaystyle <\ text <Конечное значение>> = <\ text <начальное значение>> \ times e ^ > t>>

где — непрерывная норма прибыли, а — продолжительность времени. р л о грамм <\ displaystyle r _ <\ mathrm >> т <\ displaystyle t>

Пример 2

В течение десятилетия портфель растет с постоянной доходностью 5% годовых (в год) в течение трех из этих лет и 10% годовых в течение остальных семи лет.

Конечное значение знак равно начальное значение × е 0,05 × 3 × е 0,10 × 7 <\ displaystyle <\ text <Конечное значение>> = <\ text <начальное значение>> \ times e ^ <0,05 \ times 3>\ times e ^ <0,10 \ times 7>> знак равно начальное значение × е ( 0,05 × 3 10 + 0,10 × 7 10 ) × 10 <\ displaystyle = <\ text <начальное значение>> \ times e ^ <\ left (0,05 \ times <\ frac <3><10>> + 0,10 \ times <\ frac <7><10>> \ right) \ times 10>>

Непрерывная взвешенная по времени ставка доходности за десятилетний период — это средневзвешенная по времени величина:

5 % × 3 10 + 10 % × 7 10 знак равно 5 % × 3 + 10 % × 7 10 знак равно 8,5 % <\ displaystyle 5 \% \ times <\ frac <3><10>> + 10 \% \ times <\ frac <7><10>> = <\ frac <5 \% \ times 3 + 10 умножить на 7><10>> = 8,5 \%>

Обычная ставка доходности, взвешенная по времени

Пример 3

Рассмотрим другой пример, чтобы рассчитать среднегодовую норму прибыли за пятилетний период для инвестиций, которые приносят 10% годовых в течение двух из пяти лет и -3% годовых для трех других. Обычная взвешенная по времени прибыль за пятилетний период составляет:

( 1 + 0,10 ) ( 1 + 0,10 ) ( 1 — 0,03 ) ( 1 — 0,03 ) ( 1 — 0,03 ) — 1 <\ displaystyle (1 + 0.10) (1 + 0.10) (1-0.03) (1-0.03) (1-0.03) -1> знак равно 1.1 2 × 0,97 3 — 1 <\ displaystyle = 1.1 ^ <2>\ times 0.97 ^ <3>-1> знак равно 0,104334 … <\ displaystyle = 0.104334 \ ldots> знак равно 10,4334 … % <\ displaystyle = 10,4334 \ ldots \%>

а после пересчета в годовом исчислении норма доходности составляет:

( 1.1 2 × 0,97 3 ) 1 / ( 2 + 3 ) — 1 <\ Displaystyle (1,1 ^ <2>\ раз 0,97 ^ <3>) ^ <1 >— 1> знак равно 1.0200 … — 1 <\ displaystyle = 1.0200 \ ldots -1> знак равно 2,00 … % па <\ displaystyle = 2,00 \ ldots \% <\ text >>

Период времени, в течение которого норма доходности составляла 10%, составлял два года, что выражается в степени двойки в множителе 1,1:

Аналогичным образом, норма доходности за три года составила -3%, что является степенью тройки при коэффициенте 0,97. Затем результат рассчитывается в годовом исчислении за весь пятилетний период.

Измерение эффективности портфеля

Инвестиционные менеджеры оцениваются по инвестиционной деятельности, которая находится под их контролем. Если они не контролируют сроки потоков, то компенсация времени потоков с применением метода истинной взвешенной по времени доходности к портфелю является лучшим показателем эффективности инвестиционного менеджера на уровне всего портфеля.

Внутренние потоки и производительность элементов в портфеле

Внутренние потоки — это операции, такие как покупка и продажа холдингов в портфеле, в которых денежные средства, использованные для покупок, и денежная выручка от продаж также содержатся в том же портфеле, поэтому внешний поток отсутствует. Денежный дивиденд на акцию в портфеле, который сохраняется в том же портфеле, что и акция, представляет собой поток от акции на денежный счет в портфеле. Он является внутренним по отношению к портфелю, но внешним по отношению как к счету акций, так и к счету денежных средств, когда они рассматриваются индивидуально, изолированно друг от друга.

Метод, взвешенный по времени, учитывает только эффект, связанный с размером и сроками внутренних потоков в совокупности, т. Е. В той мере, в какой они приводят к общей эффективности портфеля. Это происходит по той же причине, что взвешенный по времени метод нейтрализует влияние потоков. Следовательно, он не учитывает производительность частей портфеля, например производительность, обусловленную индивидуальными решениями на уровне безопасности, настолько эффективно, насколько эффективно отражает общую производительность портфеля.

Взвешенная по времени доходность конкретной ценной бумаги, от первоначальной покупки до возможной окончательной продажи, одинакова, независимо от наличия или отсутствия промежуточных покупок и продаж, их сроков, размера и преобладающих рыночных условий. Он всегда соответствует динамике курса акций (включая дивиденды и т. Д.). Если эта особенность взвешенной по времени доходности не является желаемой целью, она, возможно, делает метод, взвешенный по времени, менее информативным, чем альтернативные методологии для определения результативности инвестиций на уровне отдельных инструментов. Чтобы атрибуция производительности на индивидуальном уровне безопасности была значимой, во многих случаях доходность отличается от доходности цены акции. Если доход от отдельной ценной бумаги совпадает с доходом от цены акции, эффект времени транзакции равен нулю.

См. Пример 4 ниже, который иллюстрирует эту функцию взвешенного по времени метода.

Пример 4

Представим, что инвестор покупает 10 акций по 10 долларов за штуку. Затем инвестор добавляет еще 5 акций той же компании, купленных по рыночной цене 12 долларов за акцию (без учета транзакционных издержек). Затем весь пакет из 15 акций продается по цене 11 долларов за акцию.

Вторая покупка кажется неудачной по сравнению с первой. Является ли это несвоевременным очевидным из-за взвешенной по времени (периода владения) доходности акций в отрыве от денежных средств в портфеле?

Чтобы рассчитать взвешенную по времени доходность этих конкретных пакетов акций, отдельно от денежных средств, использованных для покупки акций, следует рассматривать покупку акций как внешний приток. Тогда фактор роста первого подпериода, предшествующий второй покупке, когда есть только первые 10 акций, равен:

Конечное значение начальное значение знак равно 10 × 12 10 × 10 знак равно 120 100 знак равно 1.2 <\ displaystyle <\ frac <\ text <Конечное значение>> <\ text <начальное значение>>> = <\ frac <10 \ times 12><10 \ times 10>> = <\ frac <120> <100>> = 1,2>

а фактор роста во втором подпериоде после второй покупки, когда всего имеется 15 акций, составляет:

Конечное значение начальное значение знак равно 15 × 11 15 × 12 знак равно 165 180 знак равно 0,91666 … <\ displaystyle <\ frac <\ text <Конечное значение>> <\ text <начальное значение>>> = <\ frac <15 \ times 11><15 \ times 12>> = <\ frac <165> <180>> = 0,91666 \ ldots>

Таким образом, общий коэффициент роста периода равен:

Произведение факторов роста подпериода знак равно фактор роста первого подпериода × фактор роста второго подпериода <\ displaystyle <\ text <Продукт факторов роста подпериода>> = <\ text <фактор роста первого подпериода>> \ times <\ text <фактор роста второго подпериода>>> знак равно 120 100 × 165 180 <\ displaystyle = <\ frac <120><100>> \ times <\ frac <165><180>>> знак равно 120 × 165 100 × 180 <\ displaystyle = <\ frac <120 \ times 165><100 \ times 180>>> знак равно 19 , 800 18 , 000 <\ displaystyle = <\ frac <19,800><18,000>>> знак равно 1.1 <\ displaystyle = 1.1>

а взвешенная по времени доходность за период владения составляет:

Фактор роста — 1 знак равно 0,1 знак равно 10 % <\ displaystyle <\ text <Фактор роста>> — 1 = 0,1 = 10 \%>

что то же самое, что и простой доход, рассчитанный с использованием изменения цены акции:

знак равно Конечное значение — начальное значение начальное значение знак равно 11 — 10 10 <\ displaystyle = <\ frac <<\ text <Конечное значение>> — <\ text <начальное значение>>> <\ text <начальное значение>>> = <\ frac <11-10><10>>>

Плохое время второй покупки не повлияло на эффективность инвестиций в акции, рассчитанную с использованием взвешенного по времени метода, по сравнению, например, со стратегией чистой покупки и удержания (т. Е. Покупка всех акций вначале, и удерживая их до конца периода).

Сравнение с другими методами возврата

Существуют и другие методы компенсации внешних потоков при расчете доходности инвестиций. Такие методы известны как «денежно-взвешенные» или «долларовые». Взвешенная по времени доходность выше, чем результат других методов расчета доходности инвестиций, когда внешние потоки плохо рассчитаны по времени — см. Пример 4 выше.

Внутренняя норма доходности

Один из таких методов — внутренняя норма доходности . Как и метод истинной взвешенной по времени доходности, внутренняя норма доходности также основана на принципе сложного процента. Это ставка дисконтирования, которая установит чистую приведенную стоимость всех внешних потоков и конечную стоимость, равную стоимости первоначальных инвестиций. Однако решение уравнения для определения оценки внутренней нормы прибыли обычно требует итеративного численного метода и иногда возвращает несколько результатов.

Внутренняя норма доходности обычно используется для измерения эффективности инвестиций в частный капитал , поскольку основной партнер (менеджер по инвестициям) имеет больший контроль над сроками денежных потоков, чем ограниченный партнер (конечный инвестор).

Простой метод Дитца

В методе Simple Dietz применяется принцип простой процентной ставки, в отличие от принципа сложного процента, лежащего в основе метода внутренней нормы доходности, и далее предполагается, что потоки происходят в средней точке временного интервала (или, что то же самое, что они распределяются равномерно во времени. интервал). Однако простой метод Дитца не подходит, когда такие предположения неверны, и в таком случае даст результаты, отличные от других методов.

Простая доходность Дитца двух или более различных составляющих активов в портфеле за один и тот же период может быть объединена вместе, чтобы получить простую доходность портфеля Дитца, взяв средневзвешенное значение. Веса — это начальное значение плюс половина чистого притока.

Пример 5

Применение метода Simple Dietz к акциям, купленным в Примере 4 (выше):

Простое возвращение Дитца знак равно прибыль или убыток начальное значение + 1 2 × чистый приток <\ displaystyle <\ text > = <\ frac <\ text <прирост или убыток>> <<\ text <начальное значение>> + <\ frac <1><2>> \ times <\ text <чистый приток>>>>> Прибыль или убыток знак равно конечное значение — начальное значение — чистый приток <\ displaystyle <\ text <Прирост или убыток>> = <\ text <конечное значение>> — <\ text <начальное значение>> — <\ text <чистый приток>>> знак равно 165 — 100 — 60 <\ displaystyle = 165-100-60> знак равно 5 <\ displaystyle = 5>

Простое возвращение Дитца знак равно 5 100 + 1 2 × 60 <\ displaystyle <\ text <Простой возврат Дитца>> = <\ frac <5> <100 + <\ frac <1><2>> \ times 60>>> знак равно 5 130 <\ displaystyle = <\ frac <5><130>>> знак равно 3,86 % (2 дп) <\ displaystyle = 3,86 \% <\ text <(2 dp)>>>

что заметно ниже 10% взвешенной по времени доходности.

Модифицированный метод Дитца

Модифицированный метод Dietz еще один метод , который, как простой метод Dietz, применяет простую норму принципа участия. Вместо того, чтобы сравнивать прирост стоимости (за вычетом потоков) с первоначальной стоимостью портфеля, он сравнивает чистую прирост стоимости со средним капиталом за интервал времени. Средний капитал позволяет рассчитать время каждого внешнего потока. Поскольку разница между модифицированным методом Дитца и методом внутренней нормы доходности заключается в том, что модифицированный метод Дитца основан на простом принципе процентной ставки, тогда как метод внутренней нормы доходности применяет принцип сложного процента, оба метода дают схожие результаты по сравнению с другими. короткие промежутки времени, если доходность низкая. Для более длительных периодов времени, при значительных потоках относительно размера портфеля и при невысокой доходности различия более значительны.

Подобно простому методу Дитца, модифицированная доходность Дитца двух или более различных составляющих активов в портфеле за один и тот же период может быть объединена вместе, чтобы получить модифицированную доходность портфеля Дитца, взяв средневзвешенное значение. Весом, применяемым к доходности каждого актива в этом случае, является средний капитал актива.

Пример 6

Снова обращаясь к сценарию, описанному в примерах 4 и 5, если вторая покупка происходит ровно в середине всего периода, модифицированный метод Дитца дает тот же результат, что и простой метод Дитца.

Если вторая покупка совершается раньше, чем на полпути в течение всего периода, прибыль, равная 5 долларам, остается прежней, но средний капитал больше, чем начальная стоимость плюс половина чистого притока, что делает знаменатель доходности Модифицированного Дитца. больше, чем в простом методе Дитца. В этом случае доходность модифицированного Дитца меньше, чем доходность простого Дитца.

Если вторая покупка совершается позже, чем на половине общего периода, прибыль, равная 5 долларам, остается прежней, но средний капитал меньше начального значения плюс половина чистого притока, что делает знаменатель доходности Модифицированного Дитца. меньше, чем в методе Simple Dietz. В этом случае доходность модифицированного Дитца больше, чем доходность простого Дитца.

Независимо от того, насколько поздно в течение периода происходит вторая покупка акций, средний капитал превышает 100, и поэтому доходность по модифицированному Дитцу составляет менее 5 процентов. Это все еще заметно меньше 10-процентной взвешенной по времени доходности.

Связанные методы возврата

Расчет «истинной взвешенной по времени прибыли» зависит от наличия оценок портфеля в течение инвестиционного периода. Если оценки недоступны при возникновении каждого потока, взвешенную по времени прибыль можно оценить только путем геометрического связывания доходов для смежных подпериодов с использованием подпериодов, в конце которых доступны оценки. Такой метод приблизительного взвешенного по времени метода возврата склонен к завышению или занижению истинного взвешенного по времени возврата.

Связанная внутренняя норма доходности (LIROR) — еще один такой метод, который иногда используется для аппроксимации истинной взвешенной по времени доходности. Он сочетает в себе метод истинной взвешенной по времени нормы доходности с методом внутренней нормы доходности (IRR). Внутренняя норма доходности оценивается через регулярные промежутки времени, а затем результаты геометрически увязываются. Например, если внутренняя норма доходности за последующие годы составляет 4%, 9%, 5% и 11%, то LIROR составляет 1,04 x 1,09 x 1,05 x 1,11 — 1 = 32,12%. Если регулярные периоды времени не являются годами, то либо рассчитайте версию IRR без учета годовых периодов удержания для каждого временного интервала, либо сначала рассчитайте IRR для каждого временного интервала, а затем преобразуйте каждый из них в доходность периода удержания за это время. интервал, затем свяжите эти возвраты за период удержания, чтобы получить LIROR.

Возвращает методы при отсутствии потоков

Если нет внешних потоков, то все эти методы (взвешенная по времени доходность, внутренняя норма доходности , модифицированный метод Дитца и т. Д.) Дают идентичные результаты — только различные способы обработки потоков отличает их друг от друга.

Логарифмическая отдача

Метод непрерывного или логарифмического возврата не является конкурирующим методом компенсации потоков. Это просто натуральный логарифм фактора роста. л п ( M 2 M 1 ) <\ displaystyle ln \ left (<\ frac > >> \ right)>

Сборы

Чтобы измерить доходность за вычетом комиссий, позвольте уменьшить стоимость портфеля на сумму комиссионных. Чтобы рассчитать доходность без учета комиссий, компенсируйте их, рассматривая их как внешний поток, и исключите отрицательное влияние начисленных комиссий из оценок.

Годовая доходность

Доходность и норма прибыли иногда рассматриваются как взаимозаменяемые термины, но доход, рассчитанный таким методом, как взвешенный по времени метод, является доходностью периода владения на доллар (или на какую-либо другую валютную единицу), а не за год (или другую единицу). времени), за исключением случаев, когда период владения составляет один год. Годовая нормализация, то есть переход к годовой норме доходности, — это отдельный процесс. См. Статью доходности .

Источник