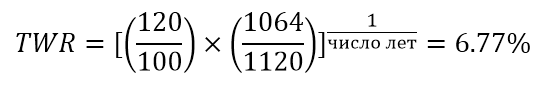Доходность twr что это

Реальная доходность портфеля: расчет и смысл

Некоторое время назад я писал статью о расчете рыночной доходности. Статья несомненно важная и рекомендуется всем, кто имеет дело с инвестициями, поскольку очень многие считают доходность либо неправильно (обычно новички, в частности путая среднеарифметические и среднегеометрические данные), либо намеренно завышают результат (обычно инвестиционные фонды, экстраполируя удачные квартальные показатели в будущее).

Тем не менее у приведенных расчетов есть недостаток. Дело в том, что разовое инвестирование одной суммы (без промежуточных вводов и выводов до выхода из рынка) это скорее гипотетический подход. Даже если не брать во внимание купонные выплаты и дивиденды, которые не всегда могут быть сразу же реинвестированы, реальное инвестирование предполагает периодические вводы и выводы средств, что плохо вписывается в представленные по ссылке формулы.

Два вида доходности: TWR и MWR

Представим такую ситуацию. Мы инвестировали в рынок 100 долларов, которые за год выросли на 20%. Соответственно, у нас на счету оказалось $120. Довольные результатом, мы вносим теперь 1000 долларов. Однако рынок ведет себя иначе: на следующий год он падает на 5%. Следовательно, наша конечная сумма оказывается равна 1120 × (1 – 0.05) = $1064. А как подсчитать полученную доходность?

В этом случае есть два способа:

• TWR (Time Weighted Return / доходность, взвешенная по времени)
• MWR (Money Weighted Retutn / доходность, взвешенная по деньгам)

Разберемся с ними отдельно.

1. TWR

Считается более традиционной, хотя это можно оспорить. Для ее расчета инвестиционный процесс разбивается на интервалы, в которых происходят ввод или вывод средств, таким образом нивелируя их влияние на результат. В нашем случае инвестиции разбиты на два равных годовых отрезка (число лет =2):

Фактически TWR отражает доходность неизменной суммы инвестора с начала инвестиций без пополнений и снятий. Но насколько логичен этот результат у нас? На первом отрезке мы заработали $20, однако на втором потеряли 1064 – 1120 = $56. Т.е. фактически у нас убыток, вызванный многократным увеличением вклада при последующем снижении рынка, а TWR считает нам плюс, игнорируя абсолютное значение взноса.

2. MWR

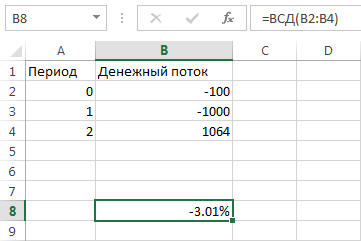
Учесть этот недостаток TWR может доходность, взвешенная по деньгам. Она отражает движение денежных средств и может быть посчитана при помощи функции ВСД в Excel. Для этого нам нужны вносимые средства со знаком «минус» и конечный результат на счете. Для случая выше расчет следующий:

Итого, MWR = – √1 + (3.01%/100%) = –1.49%. Корень означает степень ½, где 2 — число лет инвестиций. Как видно, доходность по деньгам более адекватно описывает поведение нашего реального счета, хотя для ее вычисления мы прописываем только ввод средств и конечный результат. MWR и TWR встречаются в аналитике зарубежных брокеров и в сервисах расчета инвестиционных портфелей.

CAGR (Compound Annual Growth Rate) в данном случае включает в результат все вносимые инвестором средства (ежегодно $1000), не отделяя их от рыночной доходности – поэтому результат получается заметно лучше.

Итоги

Наша ситуация вполне могла быть обратной: вначале мы получаем заметный минус на малую сумму, затем вносим гораздо больше и фиксируем небольшой плюс. Нетрудно рассчитать, что тогда TWR будет отрицательной, а MWR положительной. Можно сказать, что TWR описывает стратегию инвестора в целом, тогда как MWR включает в нее движения средств — таким образом, удачно влив крупную сумму перед периодом роста можно заметно улучшить доходность стратегии. И наоборот.

Учет инвестиций с помощью ЧИСТВНДОХ

Проблема функции ВСД в том, что она верна для периодических денежных потоков, поступающих и/или убывающих через равные промежутки времени. Однако понятно, что в реальных инвестициях ввод/вывод средств обычно происходит в спонтанном режиме. В этом случае для расчета доходности портфеля можно воспользоваться функцией ЧИСТВНДОХ.

Вся подобная статистика должна содержаться в брокерском отчете. Вычисления выполняются с помощью итерационного метода, подробное описание функции можно найти здесь .

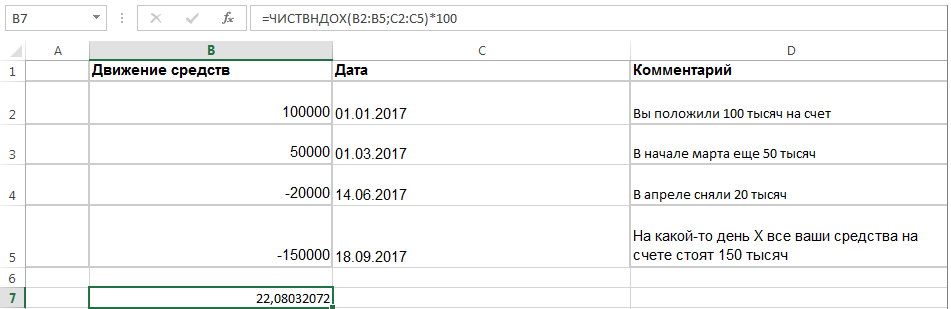
Основными в расчете являются две колонки: значений (введенных и выведенных средств) и соответствующих дат, когда происходил ввод или вывод денег. Обратите внимание, что общая стоимость активов указывается со знаком минус. После чего в произвольную ячейку, где требуется результат, нужно ставить следующую формулу:

В2:B5 — диапазон ячеек со значениями введенных или выведенных средств

С2:С5 — диапазон ячеек с датами, когда происходил ввод или вывод

Умножение на 100 позволяет получить результат в процентах. Для примера выше средняя годовая доходность будет ≈ 22.1%.

🔔 При инвестициях меньше года подобный расчет является некорректным. Кроме того, поскольку на рынке периодически возникают пузыри (доткомов на рынке США в 1995-2000 годах или российских активов на росте нефти в 2000-2008), а также бывают затяжные кризисы (обычно именно после пузырей — например Великая Депрессия 30-х или Япония после 1990 года), то для более адекватной оценки портфеля гораздо лучше подходят временные интервалы в несколько лет, чем за 1-2 года.

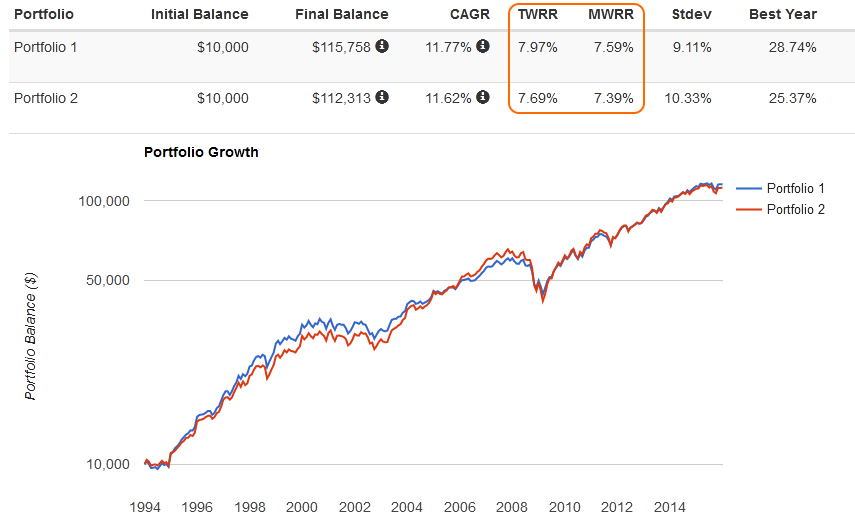
В заключении пример доходности инвестиционного портфеля одного моего клиента:

Источник

📊✅Как оценить доходность инвестиций через Interactive Brokers?

Инвестирующие через Interactive Brokers могли обратить внимание на то, что в личном кабинете этого брокера отображаются два вида доходности:

TWR — Time-Weighted Rate of Return

MWR — Money-Weighted Rate of Return

Какая между ними разница и какая доходность является правильной? Я не буду разбирать тут сложные формулы, по которым они высчитываются, а объясню принципиальную разницу в доходностях.

Итак, TWR нужен, чтобы оценить общую, совокупную доходность портфеля по инструментам, которые в него включены. По сути, это оценка доходности тех инструментов, которые есть в вашем портфеле, без привязки к точкам входа в рынок и выхода из него. Оценка доходности по TWR является наиболее объективной, если мы ведем речь об эффективности инвестиций самих по себе — без участия инвестора.

С другой стороны MWR включает в расчет доходности «человеческий фактор», так как учитывает — как, в каком объеме и когда были инвестированы средства. Соответственно, удачные вложения большого капитала на низком рынке — на просадках, коррекциях, кризисах и т.д. могут увеличить доходность по MWR и сделать ее выше, чем по TWR — как на скриншоте у Артема.

Если же напротив, моменты выбирались не слишком удачные, то TWR оказывается выше.

Если говорить в целом, то я предпочитаю смотреть на TWR — как на более объективный показатель доходности портфеля, который исключает элемент «удачи» или «мастерства» с входом в рынок. Потому что я не особо верю в эту самую удачу и идеальную точку входа.

Кроме того, наиболее объективной оценкой среднегодовой доходности я считаю самостоятельной подсчет доходности в Excel по формуле XIRR с учетом стартовой суммы капитала и пополнений. Подобное отношение связано с тем, что если вы пополняли счет у IB в валюте, отличной от доллара США, и совершали валюто-обменные операции, то в расчетах доходности по MWR TWR учитывается и доходность от изменения валютных курсов.

Источник

Что такое доходность взвешенная по времени (TWR) ?

Как правильно оценить доходность портфеля? Казалось бы, что может быть проще: смотрим на текущую оценку стоимости портфеля, делим на сумму внесенных средств и получаем результат. Однако не всё так однозначно.

Начнем с самого простого варианта. Представим, вы вложили 100 долларов и через год получили 110. Тут всё ясно: делим 110 на 100 и получаем 1,1, то есть +10%. Это доходность портфеля за год.

Усложняем задачу. Предположим теперь, что вы вложили опять же 100 долларов, но теперь на два года, и в конце срока получили 120 долларов. Определить доходность за 2 года по-прежнему легко. Делим 120 на 100 и получаем 1,2, то есть вложение прибавило 20%. Тут никаких проблем нет, но как сравнить два вложения, которые были сделаны на разные сроки? Например, мы хотим сравнить результат с альтернативной инвестицией, которая за 3 года выросла на 30%. Что лучше, первый вариант или второй?

Для того, чтобы ответить на этот вопрос, надо получить доходность, приведенную к году (в англоязычных отчетах все приведенное к году обозначают словом “annualized”). И тут возникает интересная тонкость. Можно использовать 2 вида средних: среднее арифметическое и среднее геометрическое.

В условиях нашего первого примера, среднее арифметическое будет 10% в год (20% деленное на 2 года), а вот для среднего геометрического надо взять корень второй степени из 1,2, и доходность получится уже не 10%, а 9,54%.

Казалось бы просто, однако эта тонкость приводит к поразительному количеству недоразумений, а иногда и сознательных искажений. Особенно это характерно для случаев, когда говорится что-то вроде: средняя историческая доходность данного финансового инструмента столько-то процентов в год. Тут полезно уточнить, о каком среднем идет речь. Так, например, для индекса S&P500 в период с января 1985 года по март 2020 средняя арифметическая доходность равна 11,71% в год, а средняя геометрическая 10,45%. Очень даже ощутимая разница в 1,26 процентных пункта, особенно на интервале в 35 лет.

Еще один пример: представим, что по некоторой инвестиции доходность в первый год +10% а во второй год -10%. Среднее арифметическое ноль, то есть инвестор как будто остался при своих, а вот среднее геометрическое будет 0,995. То есть инвестор на самом деле имел отрицательную доходность и терял 0,5% в год (в среднем геометрическом).

Замечу, что в англоязычной практике для средней геометрической доходности используется термин CAGR (Compound Annual Growth Rate), так что если вы видите это обозначение, то речь однозначно идет о среднем геометрическом. Если же говорится о некотором просто среднем, без уточнения, то иногда полезно выяснить, что под этим подразумевается.

Доходность при наличии пополнений и изъятий

Добавим еще одну сложность: что если по портфелю было движение денежных средств? То есть, к примеру, инвестор вложил 100 долларов, потом через год добавил еще 100, и в итоге через 2 года оценочная стоимость его инвестиций составляет, скажем, 220 долларов.

Если по-деревенски просто взять конечную сумму портфеля (220 долларов) и поделить на сумму пополнений (которые составили 200 долларов), то получится 1,1, то есть +10% за два года, или если в год (среднегеометрически) CAGR 4,88%. Однако это не верно.

На самом деле, на этот вопрос есть 2 ответа, и оба они правильные. Можно посчитать доходность, взвешенную по деньгам (Money Weighted Retutn — MWR) или доходность, взвешенную по времени (Time Weighted Return — TWR) . Для каждого инвестора очень полезно знать, чем они отличаются, а отличаться они могут радикально.

Итак, доходность, взвешенная по деньгам — это то же самое, что IRR. Никаких отличий. Для того, чтобы понять, что она означает, представьте депозит без ограничений на снятие и пополнение с непрерывным начислением и выплатой процентов (каждый день или даже каждую минуту). Представьте теперь, что доходность этого волшебного депозита неизвестна. Так вот, доходность, взвешенная по деньгам (она же IRR, она же MWR) — это такая доходность, при которой депозит становится неотличим от анализируемой инвестиции. Подробнее в другой моей статье.

В чём недостаток доходности, взвешенной по деньгам? Поясню на примере. Предположим, у нас есть инвестиция с негарантированной доходностью, такая, как фондовый рынок, на котором год на год не приходится.

Допустим, некоторый воображаемый инвестор в начале года инвестировал в некую стратегию 100 долларов. Год был удачный, и к концу года 100 долларов превратились в 120, или даже в 130. Инвестор обрадовался такому успеху, побежал в банк, снял там деньги с депозита и в начале второго года инвестировал в стратегию еще 1000 долларов. То есть увеличил свои вложения почти в 10 раз.

Однако не всё коту масленица, как уже говорилось выше, на фондовом рынке год на год не приходится, и по результатам второго года рынок не вырос, а наоборот упал. Упал не очень сильно — всего на 5%.

Стратегия показала +30% в первый год и -5% во второй. Среднее геометрическое +11,13% в год (посчитать легко 1,3х0,95, из этого корень и минус единица). Отличный результат. Среднее арифметическое 12,5% в год — еще лучше.

Тем не менее, что мы видим у нашего инвестора по результатам 2 лет инвестирования? В конце первого года оценка его портфеля составляла 130 долларов. После чего он добавил еще 1000, и оценка стала 1130. По окончанию второго года, в результате падения на 5% портфель с 1130 долларов сократился и составляет 1073,5. Теперь, если мы для этого портфеля посчитаем MWR, то получим убыток в 2,21% в год!

В чём подвох? Как прибыль по одному методу расчета превратилась в убыток по другому? Какая цифра правильная? К сожалению, правильные обе. Дело в том, что после первого года инвестор очень сильно увеличил свой счет. Это привело к тому, что даже небольшой убыток (в относительном выражении) перечеркнул все прибыли прошлых лет (в абсолютном выражении) и увел портфель в целом в минус.

Цифра, которую мы посчитали в первый раз (+11,13%), это и есть доходность, взвешенная по времени (TWR) . Это та доходность, которую получил бы инвестор, если бы держал на счету одну и ту же сумму, без снятий и пополнений. Цифра, которую мы посчитали во второй раз (-2,21%), это доходность, взвешенная по деньгам. Тот результат, который инвестор получил на самом деле.

Как видно из примера выше, эти две цифры могут различаться радикально, вплоть до того, что по одной метрике прибыль, а по другой убыток. Легко придумать пример, в котором инвестору, наоборот, повезло, и он увеличил свой счет перед взлетом (или уменьшил перед провалом). Тогда ситуация будет обратной, TWR будет в минусе, а MWR в плюсе. Для оценки результата инвестирования важно смотреть на обе эти цифры.

В целом принято считать, что доходность, взвешенная по времени, больше характеризует инвестиционную стратегию, а доходность, взвешенная по деньгам, включает в себя частично стратегию и частично влияние обстоятельств. Но на самом деле, оба этих показателя представляют собой что-то, сформированное совместным действием замысла и случая.

Доходность с поправкой на риск

Понятие доходности с поправкой на риск очень важно для каждого инвестора. Для того, чтобы пояснить, что это, такое начну с гипотетического житейского примера.

Представьте, что вам показали объявление о приеме на работу. Должность генерального директора некоторого ООО с ничего не говорящим названием. Работа в офисе в Москве, особых знаний и умений не требуется. Зарплата, ну допустим, 400 тыс. рублей в руки в месяц.

Оформление по ТК (8-часовой рабочий день, отпуск, всё по закону). Как вы думаете, хорошее предложение?

На первый взгляд, предложение не плохое, однако вы, вероятно, уже почувствовали подвох. После прочтения сразу вспоминается старый анекдот: серьезная компания ищет на работу главного бухгалтера, график работы — год через трое.

Действительно, многим организациям нужны директора (и учредители, кстати, тоже), главная функция которых в том, что они потом будут сидеть в местах не столь отдаленных. Ну или по крайней мере получат судимости и условные сроки за экономические преступления.

Посмотрим на объявление еще раз. Является ли предложенная зарплата адекватной компенсацией риска “присесть” на пару-тройку лет? Для кого-то может быть да, но совершенно очевидно, что предложение уже становится другим. Гораздо менее привлекательным.

Разовью идею еще дальше, предположим, что деятельность упомянутого выше ООО не просто не законна, но глубоко криминальна. Настолько, что дальнейшим развитием карьеры директора может быть даже не уголовное дело, а отбытие на кладбище. Что вы думаете о предложенной работе теперь?

Опять же, я уверена, найдутся те, кого оно устраивает и в таком виде, но моя ключевая идея в том, что добавление информации о возможном уголовном деле или о риске для жизни кардинально меняет привлекательность предложения. В этом и есть разница между просто доходностью и доходностью с поправкой на риск.

Давайте вернемся к финансовым инструментам. Предположим, вам предлагается по номиналу облигация с доходностью 10% годовых в долларах и сроком до погашения 10 лет. Хорошее это предложение или нет? На момент написания статьи 10-летние облигации казначейства США торгуются с доходностью 0,73% годовых, и кажется, что 10% в год — это просто космос. Но так же, как и в примере с предложением о работе, давайте не будем спешить с выводами.

Дополнительная информация: облигация идет с 50% вероятностью полной потери капитала (то есть кредитный рейтинг примерно в группе “С”). Что получается тогда? Если предельно упрощённо, есть 2 варианта:

• Дефолта нет, и вы получаете 159,37% прибыли за 10 лет (вероятность 50%).
• Произошел дефолт, и вы полностью потеряли вложение (вероятность 50%).

В итоге мы получаем, что с учетом вероятности дефолта ожидаемая доходность составит 29,68% за 10 лет (0,5х2,5937+0,5х0=1,2968), то есть в среднем 2,6% годовых. Уже не так интересно, не так ли?

Да, для продвинутых читателей оговорюсь, что расчет выше был сугубо “на пальцах”. Если подходить серьезно, то надо считать вероятность дефолта на каждом году, возможность возврата части вложений, реинвестицию купона и т. д. Но тут главное — качественная картина, а не безупречная точность.

Итак, возвращаемся к нашим облигациям. Еще раз результат, к которому мы пришли: номинальная доходность в 10% годовых с учетом риска дефолта превратилась в гораздо более скромные 2,6%. Это и есть разница между номинальной доходностью и доходностью с поправкой на риск.

Количественная оценка доходности с поправкой на риск — это большая тема, так что тут я ограничусь чисто концептуальными примерами, приведенными выше. Замечу только, что тут всё тоже неоднозначно и на этот вопрос есть разные точки зрения, которые могут привести к разным результатам. Ну или если точнее — есть ряд подходов, каждый из которых имеет свои недостатки и ограничения, но ограниченная теория с недостатками — это лучше, чем ничего. Об этом другая моя статья, которая, правда, требует для понимания несколько более продвинутой подготовки.

Источник