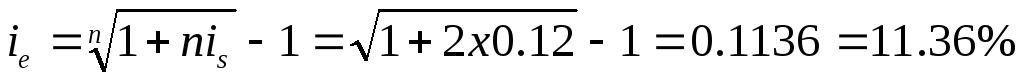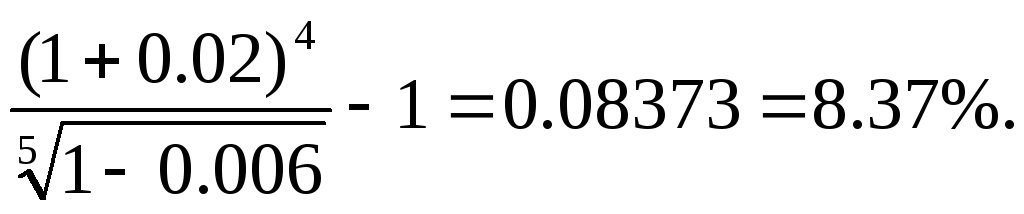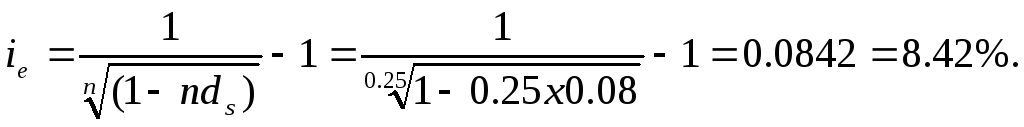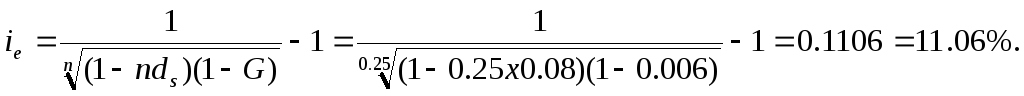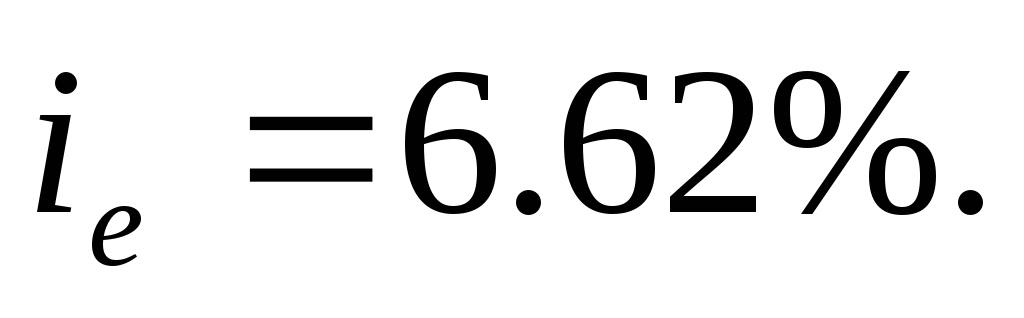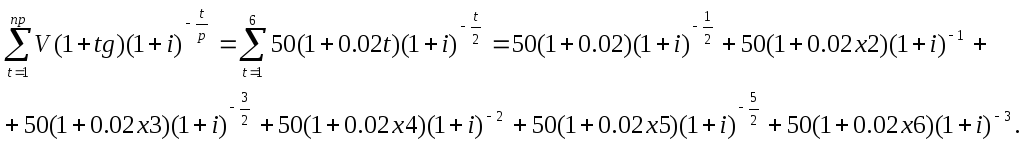Доходность сделки для кредитора
Определение процентной ставки
Уровень процентной ставки является мерой доходности операции, критерием сопоставления альтернатив и выбора наиболее выгодных условий. Из формул
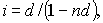
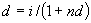
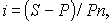
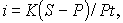
 (3)
(3)
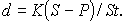
Следует отметить, что срок п, t в этих формулах имеет разный смысл: в (1) и (2) это весь срок операции, а в (3) и (4) — оставшийся срок до погашения.
Определить доходность операции для кредитора, если им предоставлена ссуда в размере 200 тыс. р. на 60 дней и контракт предусматривает сумму погашения долга 210 тыс. р. Доходность выразить в виде простой ставки процентов i и учетной ставки d. Временную базу принять равной К = 360 дней.
По формуле (2.) определим доходность операции в виде простой ставки процентов:
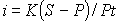
По формуле (4) определим доходность операции в виде простой учетной ставки:
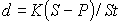
Доходность операции, выраженная в виде простой ставки составляет 30%, а в виде простой учетной ставки – 28,6%.
Источник
Доходность контракта для кредитора
Рассмотрим способы измерения доходности финансово кредитной операции для кредитора – одного из двух основных участников контракта.
Доход от выдачи кредита кредитор получает в виде процентов от выданной ссуды, комиссионных, дисконта при учете векселей и т.п. Доходность операции обычно измеряется годовой ставкой сложных (реже – простых) процентов, когда все вложения и доходы рассматриваются как эквивалентная им ссудная операция (иногда применяются и другие показатели доходности). Такую ставку называют эффективной процентной ставкой ie.
Рассмотрим, как определяется доходность некоторых финансовых операций.
1. Ссуда выдана под простые проценты по ставке is или под сложные проценты по ставке jm, или осуществляется учет финансовых документов (векселей) по простой ds или по сложной dc, или по учетной ставке fm. Во всех этих случаях доходность операции определяется эквивалентной ставкой ic сложных процентов.
2. Ссуда в размере Р выдана на n лет под простые проценты по годовой ставке is. Это означает, что заемщик через n лет должен вернуть сумму P(1+n is). При выдаче ссуды были удержаны комиссионные в размере G% от суммы кредита, то есть была получена сумма (P—PG). Будущая стоимость этой суммы равна
Доходность операции ieопределяется из условия равенства возвращаемой заемщиком суммы и будущей стоимости полученной суммы:
Сократив на P и разделив обе части уравнения на 1-G, получим уравнение


Ссуда выдается сроком на 2 года под 12 % простых годовых. Определить доходность этой операции при следующих условиях:
А) комиссионные не взимаются ;
Б) удерживаются комиссионные в размере 0,5% от суммы ссуды;
В) удерживаются комиссионные в размере 0,5% от суммы ссуды и срок ссуды увеличен до 4 лет.
А) Доходность операции определяем по формуле:
Б) Доходность операции определяем по формуле:
В) Доходность операции определяем по формуле:
Рассмотренный пример показывает, что для кредитора взимание комиссионных увеличивает доходность сделки, а увеличение срока ссуды уменьшает ее доходность.
3. Ссуда в размере P выдана под ставку процентов 






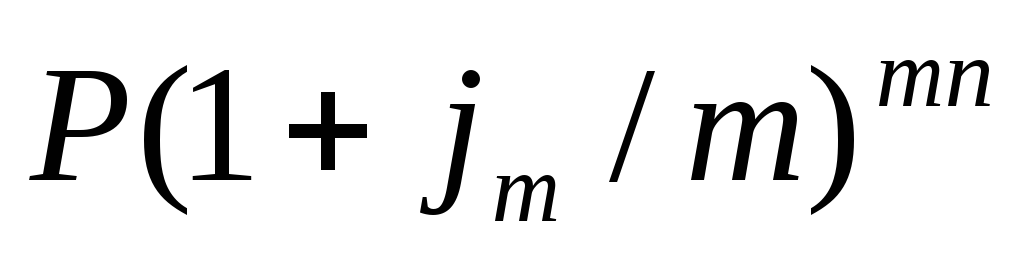
Сократив на Р и разделив обе части уравнения на 

откуда получаем формулу для вычисления 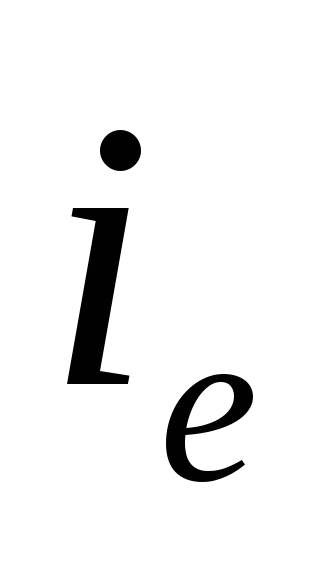

Ссуда выдается сроком на 5 лет по ставке 
А) комиссионные не взимаются;
Б) удерживаются комиссионные в размере 0,6% от суммы ссуды;
В) удерживаются комиссионные в размере 0,6% от суммы ссуды и срок ссуды увеличен до 10 лет.
А) Доходность операции определяем по формуле:
Б) Доходность операции определяем по формуле:

В) Доходность операции определяем по формуле:

Как и в предыдущем примере замечаем, что взимание комиссионных увеличивает эффективность сделки для кредитора, а увеличение срока ссуды уменьшает ее эффективность.
4. Банк учитывает вексель на сумму 






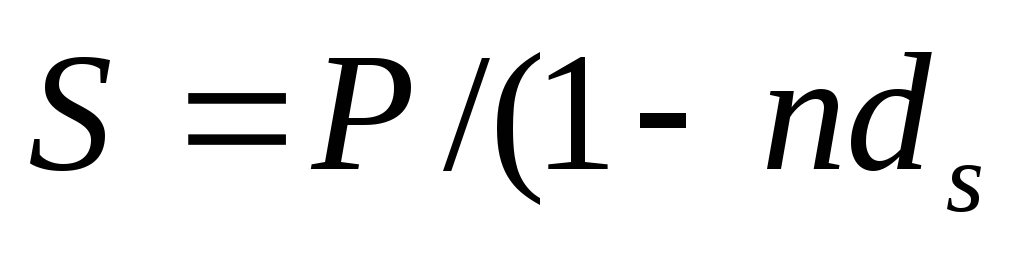

которая является суммой, наращенной на реальную плату за вексель, если на эту сумму начисляется 


Решив это уравнение относительно 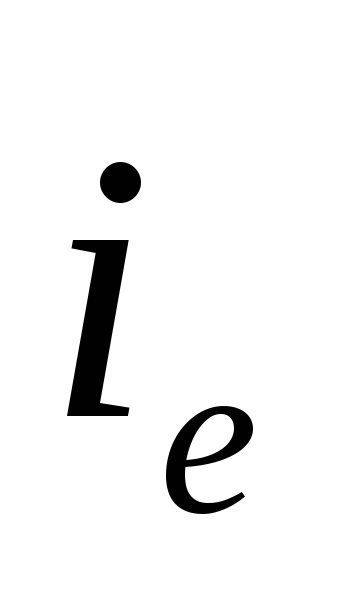
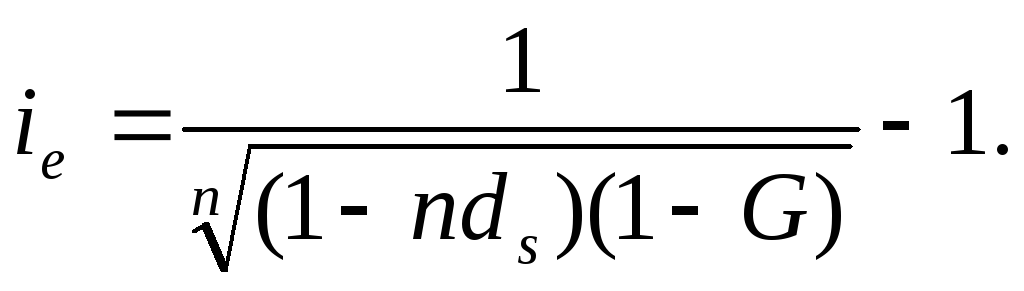
Банк учитывает вексель за 3 месяца до срока его оплаты по простой учетной ставке 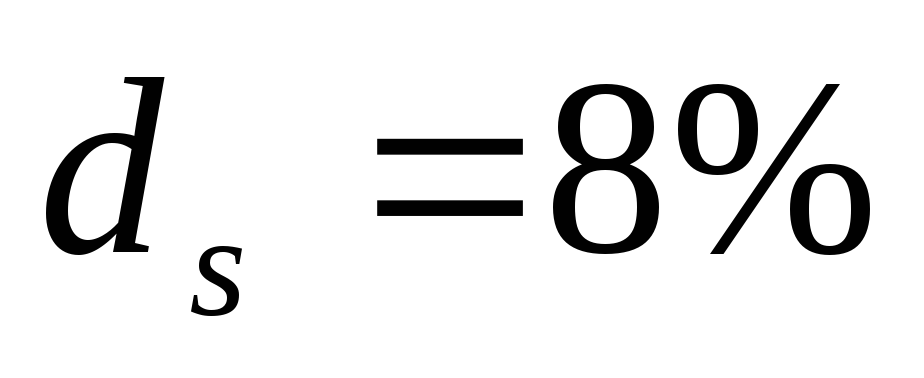
А) комиссионные не взимаются;
Б) удерживаются комиссионные в размере 0,6% от суммы, выплачиваемой за вексель;
В) удерживаются комиссионные в размере 0,6% от суммы, выплачиваемой за вексель, и период времени до оплаты векселя — 6 месяцев.
А) Доходность операции определяем по формуле:
Б) Доходность операции определяем по формуле:
В) Доходность операции определяем по формуле:
Мы видим, что взимание комиссионных повышает доходность учета для банка, а увеличение срока от момента учета до момента оплаты векселя уменьшает доходность учета.
5. Продавец продал товар, стоимость которого равна С, получив в уплату несколько векселей (портфель векселей), каждый из которых выдан на сумму 





Найдем сначала сумму 

За вексель, погашаемый первым (через 

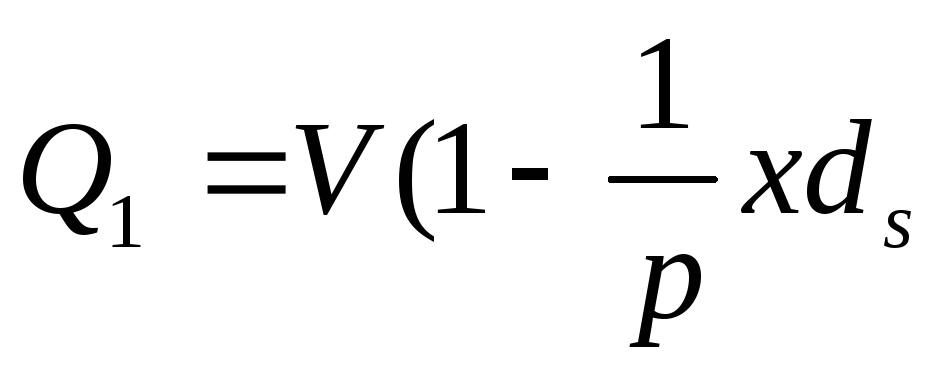
За вексель, погашаемый вторым (через 

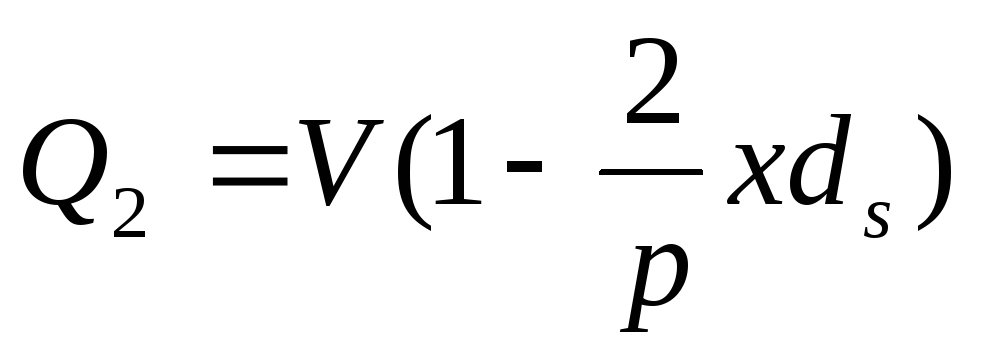
Продолжая аналогичным образом, получаем на последнем шаге:
За вексель, погашаемый последним (через 

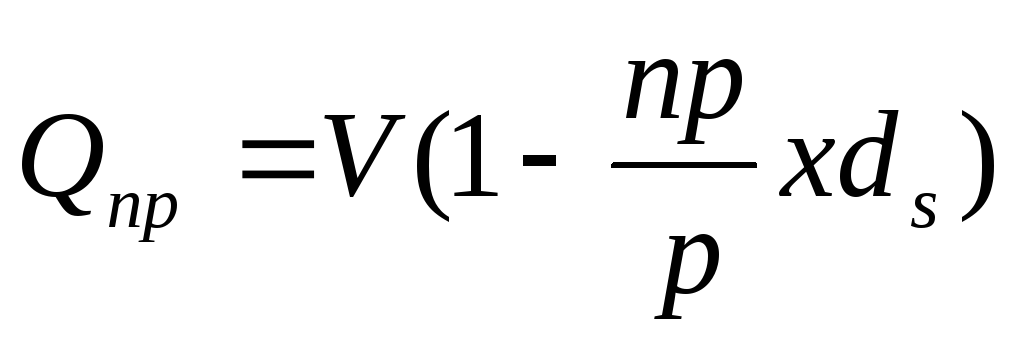
За весь портфель векселей банк выплатит сумму 

Выполнив суммирование , получаем формулу :


Погашая эти вексели, банк получает р-срочную ренту, состоящую из р платежей ежегодно в течение 



Эффективная ставка сложных процентов 

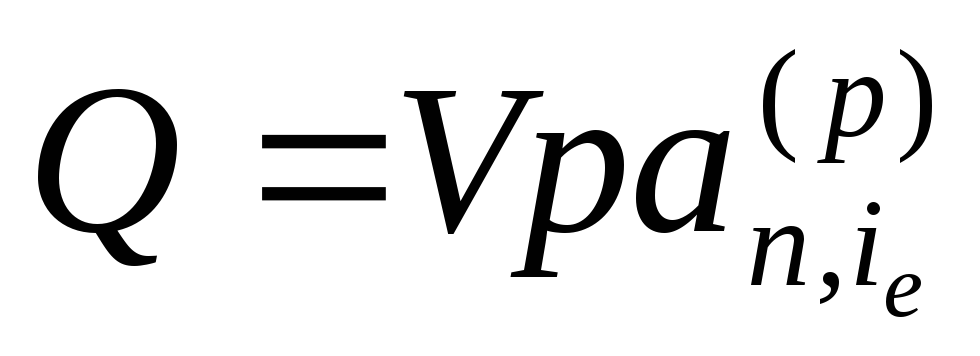
Следовательно, для нахождения 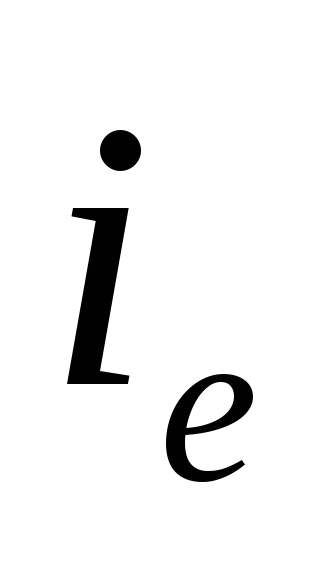

Банк учитывает портфель, состоящий из 12 векселей по 100 тыс. руб. каждый, погашаемый ежеквартально. Простая учетная ставка банка равна 6%. Определить доходность этой операции для банка.
Вычислим сначала сумму 
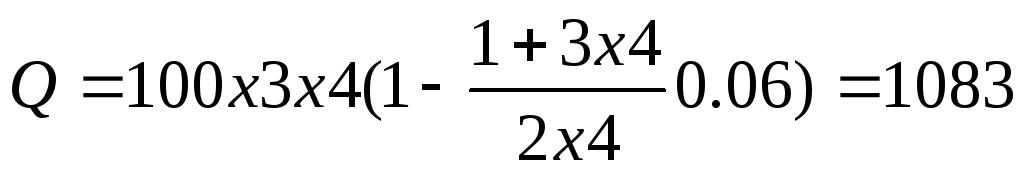
Для нахождения 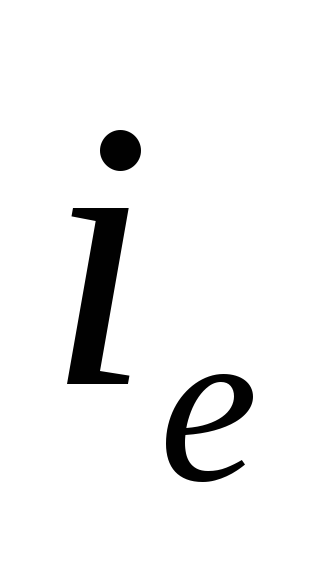

Используя в электронных таблицах Excel команду “Подбор параметра”, можно найти значение эффективности ставки сложных процентов
6. Рассмотрим случай, отличающийся от случая 5 лишь тем, что векселя , составляющие портфель , выданы не на одинаковые суммы , а на суммы , возрастающее с увеличением промежутка времени от момента учета до момента оплаты векселя по правилу простых процентов. Точнее , если t-номер векселя в порядке его оплаты (t=1,2…np) , то на t-ом векселе указана сумма 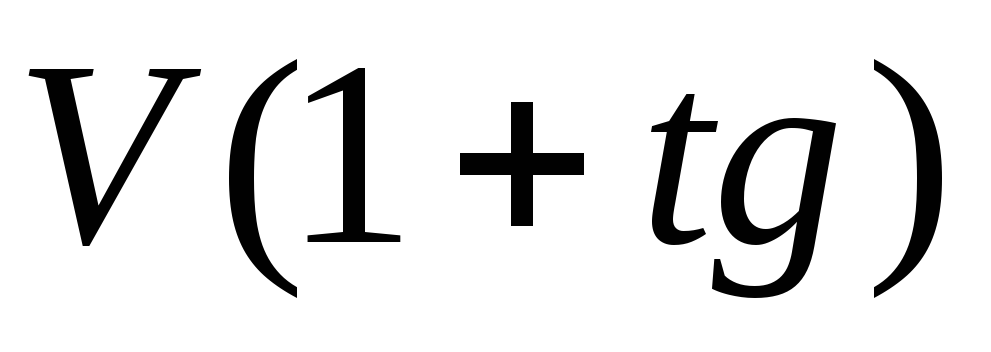

Сначала рассчитаем сумму , которую должен выплатить банк при учете этого портфеля по простой учетной ставке 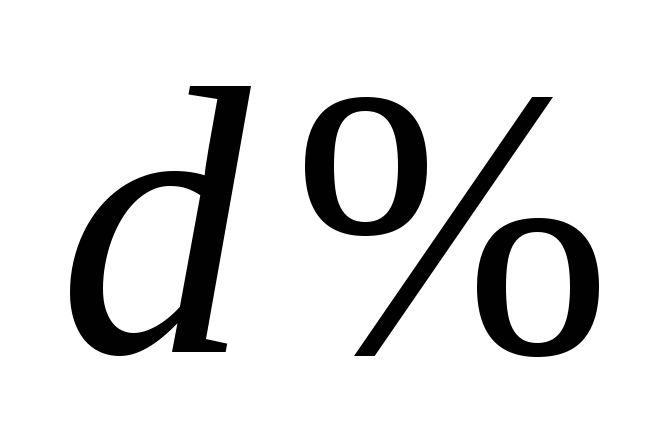
За первый вексель на сумму 

За второй вексель на сумму 

Продолжая аналогичным образом , получаем на последнем шаге :
За последний 

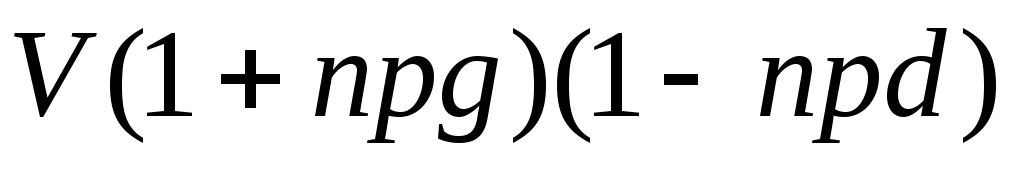
Сумма 
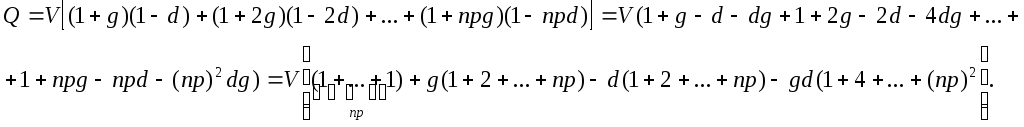


С учетом этих формул выражение для 
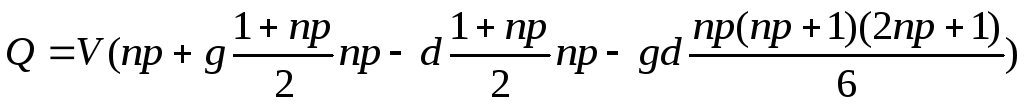
Преобразуем его и получим формулу :

Oбозначив через i ставку сравнения, найдем современные ценности сумм; которые получит банк; предъявив векселя портфеля к оплате:
• для первого векселя: PV = V(l +g)(1+ i) -1/ p ;
• для второго векселя: PV = V(1+ 2g)(1 + i) -2/ p ;
Продолжая аналогичным образом, получаем на последнем шаге:
• для nр-го векселя: PV = V(1 + npg)(1 + i) — np / p .
Эффективную ставку ie естественно искать из условия равенства современной ценности суммы, полученной банком при предъявлении векселей портфеля к оплате, и суммы, выплаченной банком при учете портфеля векселей:

Это уравнение можно решить любым из обсуждавшихся ранее методов. Рассмотрим пример.
Банк учел по простой учетной ставке 8% годовых портфель, состоящий из 6 векселей, каждый на 50 тыс. руб. плюс 4% простых годовых. Векселя погашаются по полугодиям. Найти доходность этой операции.
Найдем по формуле (8.8) сумму, выплаченную банком при учете портфеля, при V = 50, р = 2, n= 3, g = 4%/2 = 2% = 0.02, d = 8%/2 = 4% =. 0.04:
Вычислим суммарную современную ценность суммы, которую банк получит при предъявлении векселей портфеля к оплате:
Подставляя полученное значение в уравнение (8.9), имеем:
Введем обозначение: (1 +i) -l = х. Тогда последнее уравнение примет вид.
51х 1/2 + 52х + 53х 3/2 + 54х 2 + 55х 5/2 + 56х 3 = 275.36.
Решив это уравнение любым из обсуждавшихся ранее методов, найдем значение корня уравнения: х =0.916. Далее находим iе из условия:
Выполнив необходимые арифметические вычисления, получаем:
Такова доходность операции учета банком данного портфеля векселей.
8.7. Доходность портфеля облигаций
Покупатель облигаций может составить портфель, состоящий из облигаций, различных по номинальной стоимости, срокам погашения и условиям выплаты процентов. Причина формирования портфеля из различных финансовых инструментов лежит в идее диверсификации риска. Здесь под риском мы понимаем отклонение доходности финансового инструмента oт
среднего значения доходности. Концепция управления портфелем фондовых актинов (ценных бумаг) лежит в основе современной теории финансов. Мы не касаемся этого сложного вопроса в нашей книге — ему посвящена специальная литература. Однако расчет доходности портфеля (в отличие от расчета риска) вполне элементарен, этим мы сейчас и займемся.
Доходность портфеля облигации для владельца портфеля измеряется ставкой сложных процентов iе, при которой современная ценность всех выплат, полученных но облигациям портфеля, равна сумме затрат на приобретение облигаций, составляющих портфель. То есть величина iе определяется из уравнения:
t — сроки получения выплат но облигациям,
Rt — величина выплаты в момент t,
nj — число облигаций j-го вида в портфеле,
Qj— цена, по которой была куплена облигация j-го вида.
Приобретен портфель облигаций трех видов: А, Б и В. Определить доходность этого портфеля для его владельца. В следующей таблице приведены данные об облигациях, входящих в портфель, и условиях приобретения этих облигаций владельцем портфеля:
Источник
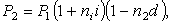
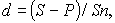 (3)
(3)