Доходность рассчитывается по рыночной стоимости

Как посчитать доходность облигаций?

Я хочу попробовать вложиться в облигации, но раньше пользовался только вкладами. Там все понятно, ставка указана в договоре.

В облигациях все выглядит сложнее. Расскажите, пожалуйста, как правильно посчитать доходность по облигации. Она зависит только от размера купона или нет?

Облигации — полезный вид ценных бумаг: доход по ним выше, чем по вкладам. Однако сами по себе эти ценные бумаги сложнее. Давайте разбираться, какие бывают виды доходностей, от чего зависит их величина и как это все посчитать.

Типы облигаций по форме выплаты

Чаще всего встречаются купонные облигации. Купон — это выплата процентов, которая происходит с определенной периодичностью: например, раз в полгода. Даты выплат известны заранее, а вот размер купонов может со временем меняться.

Также бывают дисконтные ценные бумаги: по ним не выплачиваются купоны, но сами бумаги продаются заметно дешевле номинала. Доход можно получить, если цена вырастет или если погасить облигацию по номиналу в конце срока.

Облигации с купоном популярнее, поэтому рассмотрим их на примере типичного представителя — ОФЗ-26217 с погашением 18 августа 2021 года. По состоянию на 2 октября эта облигация стоит 99,3% от номинала, то есть 993 рубля.

Купонная доходность

Это деньги, которые эмитент обязан периодически платить владельцам облигаций. Процентную ставку доходности облигации с купоном посчитать легко:

(Годовые купоны / Номинал) × 100%

Номинал облигации ОФЗ-26217 — 1000 рублей, выплаты производятся каждые полгода в размере 37,4 рубля. Купонная доходность — 7,5% в год.

Облигации далеко не всегда продаются по номиналу: их цена меняется со временем. Поэтому расчет купонной доходности не позволяет точно узнать, сколько инвестор заработает на облигациях.

Текущая доходность

Это более точный показатель, при расчете которого используется не номинал, а чистая цена, — без накопленного купонного дохода. НКД — это часть купона, которая накопилась, но еще не выплачена. Покупая облигацию, нужно заплатить ее владельцу НКД — это как компенсация за то, что он продает ценную бумагу, не получив купон. Зато новый владелец получит весь купон в дату выплаты.

Величина текущей ставки показывает, какой денежный поток дает облигация, купленная по определенной цене.

Формула выглядит так:

(Купонный доход за год / Чистая цена) × 100%

Доходность ОФЗ-26217 равна (74,8 / 993) × 100%, или 7,53% годовых.

Этот показатель выше купонной ставки, так как цена ОФЗ-26217 ниже номинала. Если бы эта ОФЗ стоила дороже номинала, текущая доходность была бы ниже купонной.

Простая доходность к погашению

Многие держат облигации до даты их погашения, когда вместе с последним купоном инвестор получает номинал. Но рассчитать величину доходности облигации на момент погашения можно лишь тогда, когда известен размер всех купонов.

Ставка к погашению рассчитывается по более сложной формуле:

((Номинал − Полная цена покупки + Все купоны за период владения) / Полная цена покупки) × (365 / Количество дней до погашения) × 100%

У ОФЗ-26217 простая доходность к погашению составит ((1000 − 1001,2 + 224,4) / 1001,2) × (365 / 1051) × 100% = 7,74% годовых.

Эффективная доходность к погашению

Если использовать полученные купоны для покупки дополнительных ценных бумаг, можно посчитать ставку дохода по облигациям с реинвестированием купонов — примерно как вклад с капитализацией процентов.

Считается, что купоны вкладываются в новые бумаги по текущей ставке — той, что была первоначально. Это допущение, так как цена меняется со временем и фактическая доходность будет отличаться.

Реинвестировать купон можно, если полученного дохода от купонов хватает на покупку дополнительных ценных бумаг. Получив 37,4 рубля в виде купона по одной ОФЗ-26217, часть облигации федерального займа купить не удастся. А вот если иметь 100 таких бумаг, купонная выплата будет 3 740 рублей. Этого хватит на 3 дополнительные ценные бумаги — и еще останется.

Простой и точный способ узнать эффективную доходность к погашению — воспользоваться облигационным калькулятором на сайте Rusbonds или на сайте Московской биржи. У ОФЗ-26217 этот показатель на 2 октября был равен 7,93% годовых.

Для расчета доходности с помощью облигационного калькулятора необходимо выбрать ценную бумагу из списка, указать дату приобретения и чистую цену без НКД. Калькулятор также покажет текущую и простую процентные ставки к погашению, то есть их необязательно считать вручную. При этом налоги, брокерские и депозитарные комиссии в калькуляторе не учитываются.

Нюансы и полезные советы

Цена на облигацию зависит в том числе от процентных ставок в экономике. Если Центробанк поднимет ставку, инвесторы захотят иметь инструменты с большей доходностью. Они начнут распродавать старые бумаги с постоянным купоном, и те подешевеют. Если ЦБ снизит ставку, на старые облигации вырастет спрос и они подорожают. Чем меньше времени до даты погашения, тем менее чувствительны ценные бумаги к изменениям ключевой ставки.

Выбирая между бумагами государственных займов и корпоративными, важно знать, что наибольшая доходность при прочих равных — у корпоративных облигаций. Более щедрые купоны по сравнению с государственными — это премия за риск потерять вложенные деньги, если дела у компании пойдут плохо. Если у бумаги необычно большие купоны или цена упала намного ниже номинала, значит, велики шансы лишиться денег.

Купонный доход по одним корпоративным облигациям облагается НДФЛ, по другим — нет. Список бумаг со льготным налогообложением можно посмотреть на сайте Московской биржи. Сравнивая доходность ОФЗ, корпоративных бумаг и вкладов, помните про НДФЛ.

С полученного вами НКД могут удержать налог. Лучше продавать облигацию, когда по ней выплачен купон или НКД минимальный. Также налог взимается, если продать облигацию дороже цены покупки или купить ее дешевле номинала и дождаться погашения по номиналу.

Простой вариант увеличить доход от вложений — открыть ИИС и использовать вычет на взносы. Возврат НДФЛ повысит доходность инвестиций на несколько процентных пунктов в год, а вычет можно внести на ИИС и купить дополнительные активы.

Хорошо, если брокер разрешает получать купоны на банковский счет, а не зачисляет их на ИИС. Тогда купоны можно будет самостоятельно внести на ИИС и получить потом вычет и с этих денег.

Если у вас есть вопрос о личных финансах, правах и законах, здоровье или образовании, пишите. На самые интересные вопросы ответят эксперты журнала.

Источник

Расчет рыночной доходности

Формула расчета рыночной доходности

Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.

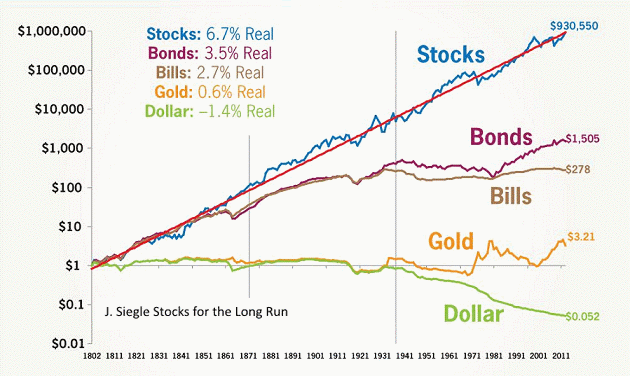
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):

Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.

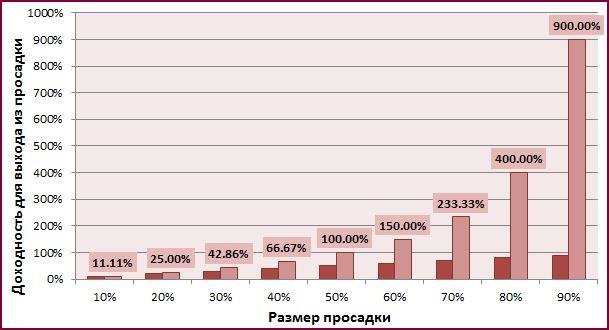
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:

Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.

В общем случае формула доходности выглядит так:

A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1

1. A(0) – исходное количество денег
2. А(n) – количество денег через n лет
3. X – годовая доходность (в процентах)

Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то

A(n) = A(n-1) × Y = A(0) × Y^n

Задача

Актив растет на 10% в год. Какова будет его доходность через 2 года?

Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу

А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)

Обратная задача

Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):

Снова принимая нашу первоначальную доходность за условную единицу, считаем:

Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%

Задача 2

За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?

Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%

Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).

Задача 3

За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?

2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда

Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%

Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.

Задача 4

Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?

Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%

Задача 5

Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.

2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%

Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:

1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)

И средняя инфляция

Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%

P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.

Задача 6

Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?

Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.

Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.

Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).

Задача 7

Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.

Y = [(7.2 + (135-120))/120] × 100% = 18.5%

Задача 8

По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:

Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%

Источник

Доходность акций: расчет и формулы

Автор: Алексей Мартынов · Опубликовано 20.10.2014 · Обновлено 28.08.2015

Инвестор может получить доход с акций двумя способами: за счет роста курсовой стоимости акций и за счет дивидендов.

Основным доходом инвестора по акциям является рост курсовой стоимости акций. Если дела у компании идут хорошо, ее выручка и прибыль растет, компания развивается, выплачивает дивиденды, которые тоже растут, это положительно отражается на цене акций, и она растет. Инвестор, видя такое положение вещей и оценив перспективы, покупает акции компании. Если дела компании продолжают идти так же хорошо, цена акций вырастает, тогда инвестор может продать акции по цене дороже и получить прибыль.

Второй источник дохода — дивиденды — это часть прибыли, которая компания выплачивает акционерам. Дивиденды могут выплачиваться раз в год, раз в полугодие или квартал. Размер дивидендов рекомендуется советом директоров и утверждается на общем собрании акционеров. Читайте, как получить дивиденды по акциям.

Доходность акций складывается из роста курсовой стоимости акций и дивидендов. Доходность акций показывает какой доход в процентом или номинальном выражении принесли акции. Доходность в общем смысле рассчитывается как сумма прибыли, деленная на сумму вложенных средств. Так как по акциям можно получить не только прибыль, но и убыток, то доходность может быть отрицательной. Рассмотрим как определить доходность акций.

Дивидендная доходность акций

Дивидендная доходность акций характеризуется отношением размера дивиденда к цене акции. Дивидендная доходность рассчитывается по формуле:

d — размер дивиденда за год
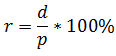
p — рыночная цена акции

Например, дивиденды по акциям Газпрома за 2013 год были равны 7,2 рубля. Цена акции 130 рублей.

Дивидендная доходность равна 7,2/130*100%=5,53%

Рыночная (текущая) доходность акций

Рыночная доходность акций, то есть за счет роста курсовой стоимости, рассчитывается по формуле:

P1 — цена продажи акции
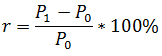
P0 — цена покупки акции

Текущая доходность акций рассчитывается также и показывает доходность, которую получит инвестор, если продаст акцию по текущей рыночной цене.

Если цена покупки акций Газпрома 120 рублей, а цена продажи 135 рублей, то доходность равна (135-120)/120*100%=12,5%.

Полная доходность акций

Полная доходность складывается из дивидендов и роста курсовой стоимости

Возьмем те же цифры, что и в предыдущем примере: (7,2 + (135-120))/120*100% = 18,5%

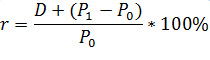
Доходность акций в процентах годовых

Владеть акцией можно как меньше, так и больше года. Поэтому, чтобы сравнить доходность акций с доходностью другого инструмента, например, депозита, ее нужно привести к равнозначному значению — доходности в процентах годовых. Для этого доходность умножается на коэффициент k=365/количество дней владения акцией. Если акцией владели 250 дней, доходность в процентах годовых рассчитывается так:

(7,2 + (135-120))/120 * 365/250 * 100% = 27,01%

Источник