Расчеты в условиях инфляции
При начислении процентов за кредит следует учитывать инфляцию. Ставку процентов при выдаче кредитов в условиях инфляции можно определить следующим образом. Если задана реальная доходность кредитной операции, определяемая простой ставкой процентов i, то для суммы кредита Р погашаемая сумма при отсутствии инфляции была бы равна:
Эквивалент такой суммы в условиях инфляции в соответствии с формулой (1.34) будет равен:
где t – уровень инфляции за срок кредита.
С другой стороны, величину St можно записать в виде:
где it – простая ставка процентов за срок кредита, учитывающая инфляцию.
Приравняв два последних выражения, получаем:
откуда простая ставка процентов, обеспечивающая реальную эффективность кредитной операции i при уровне инфляции за срок кредита t, будет равна:

Банк выдал кредит в 1 млн. руб. на год. Требуемая реальная доходность операции равна 6% годовых, ожидаемый годовой уровень инфляции принят равным 40%. Определить ставку процентов по кредиту, погашаемую сумму и сумму полученных процентов.
По формуле (2.13) ставка процентов по кредиту
it = 0,06 + 0,4 + 0,06 × 0,4 = 0,484 = 48,4%.
По формуле (2.11) погашаемая сумма
St = 5 000 000 (1 + 0,484) = 7 420 000 руб.
Сумма начисленных процентов будет равна:
I = 1 420 000 – 5 000 000 = 2 420 000 руб.
Соотношение (2.12) можно также записать в виде:
где Iи – индекс инфляции за срок кредита.
Следовательно, ставка процентов по кредиту, учитывающая инфляцию, будет равна:

Банк выдал на 9 месяцев кредит в размере 2 млн. руб. Ожидаемый месячный уровень инфляции составляет 5%, требуемая реальная доходность операции должна составить 4% годовых. Определить ставку процентов по кредиту с учетом инфляции, погашаемую сумму и сумму процентов за кредит.
Индекс инфляции за срок кредита по формуле (1.38) составит:
По формуле (2.14) ставка процентов по кредиту с учетом инфляции будет равна:
Погашаемая сумма составит:
St = 2 000 000 ( 1 + 0,75 × 0,795 ) = 3 192 500 руб.
Сумма процентов по кредиту будет равна:
I = 3 192 500 – 1 000 000 = 1192 500 руб.
Кредит 500 тыс. руб. выдается с 20 июня по 15 сентября того же года. При выдаче кредита считается, что индекс цен к моменту его погашения составит 1,3. Определить ставку процентов по кредиту, погашаемую сумму и сумму процентов, если реальная доходность кредитной операции должна быть 5% годовых и банк использует германскую практику начисления процентов.
Количество дней для начисления процентов будет равно:
11 + 30 + 30 + 15 — 1 = 85 дней.
По формуле (2.14) ставка процентов по кредиту составит:
Погашаемая сумма будет равна:
St = 500 000 [ 1 + ( 85/ 360 ) 1,34 ] = 658 194 руб.
Сумма процентов за кредит составит:
I = 658 194 – 500 000 = 158 194 руб.
При выдаче долгосрочных кредитов сложная ставка процентов it, обеспечивающая при годовом уровне инфляции t реальную эффективность кредитной операции i и определяемая аналогичным образом, будет равна:
Кредит в размере 5 млн. руб. выдается на 3 года. Реальная доходность операции должна составить 8% годовых по сложной ставке процентов, расчетный уровень инфляции составляет 10% в год. Определить ставку процентов при выдаче кредита, погашаемую сумму и сумму процентов.
По формуле (2.15) ставка сложных процентов по кредиту составит:
it = 0,03 + 0,1 + 0,03 × 0,1 = 0,133 = 13,3%.
Погашаемая сумма будет равна:
St = 5 000 000 (1 + 0,133 ) = 5 665 000 руб.
Сумма процентов за кредит составит:
7=5 665 000 – 5 000 000 = 665 000 руб.
Если задан индекс инфляции за срок кредита, ставка сложных процентов, определяемая аналогично вышеизложенному, будет равна:

Кредит 10 млн. руб. выдан на 5 лет. Расчетный индекс цен за срок кредита принят равным 3. Определить ставку процентов при выдаче кредита, погашаемую сумму и сумму начисленных процентов, если реальная доходность кредитной операции должна составить 5% годовых по ставке сложных процентов.
По формуле (2.16) ставка процентов по кредиту будет равна:
Погашаемая сумма составит:
St = 10 000 000 (1+ 0,31 ) 5 = 38 579 490 руб.
Сумма процентов за кредит будет равна:
I =38 579 490 – 10 000 000 = 28 579 490 руб.
Источник
Задача №26. Расчёт ставки процентов по кредиту с учетом инфляции
Банк выдал кредит в размере 400 тыс. руб. на срок 1,5 года.
Ожидаемый ежемесячный уровень инфляции – 0,7 %,
требуемая реальная доходность операции — 9% годовых (простые проценты).
Определите:
— ставку процентов по кредиту с учетом инфляции,
— реальную наращенную сумму и
— сумму процентных денег.
Решение:
Наращенная сумма долга без учёта инфляции (простые проценты) равна:
Реальный ожидаемый доход от операции равен 54 тыс. руб.
Определим уровень инфляции за 1,5 года. Так как ожидаемый ежемесячный уровень инфляции величина постоянная и равна 0,7 %, можно воспользоваться формулой:
Инфляция за 1,5 года предположительно составит 13,4%.
С учётом инфляции кредитор должен будет вернуть сумму равную:
FVinfl = FV * Ip = 454 × 1,1338 = 514,7381 тыс. руб.
Следовательно, банк должен назначить номинальную ставку (ставку процентов по кредиту, которая учитывает инфляцию) равную:
Найти годовую ставку процентов, учитывающую инфляцию, в случае, если период n отличен от одного года, можно также по формуле:
Сумма процентных денег за период равна:
I = 514,7381 – 400 = FVinfl – PV = 114,7381 тыс. руб.
Источник
Ставка процентов по кредиту с учетом инфляции
Список использованной литературы
Банк выдал кредит на 6 месяцев в размере 150 тыс. руб. При ожидаемом месячном уровне инфляции в 2.5% реальная доходность операции равна 24% годовых.
Определите ставку процентов по кредиту с учетом инфляции, погашаемую сумму и сумму начисленных процентов.
При выдаче кредитов уровень инфляции может быть учтен при определении ставки процентов по кредиту (брутто-ставки r). Общая формула для определения простой ставки процентов по кредиту, компенсирующей ожидаемую инфляцию, при одном периоде начисления имеет вид:
кредит ставка инфляция вексель
где r – брутто-ставка;
i – простая ставка процентов, характеризующая требуемую реальную доходность кредитной операции.
Ip – индекс инфляции за срок кредита
Индекс инфляции за срок кредита будет равен:
Следовательно, ставка процентов по кредиту с учетом инфляции:
Погашаемая сумма составит:
S =150 000(1+1,5·0,3851)=236 648 тыс.руб.
Сумма начисленных процентов:
I = S- P = 236 648 тыс.руб. – 150 000 тыс.руб. = 86 648 тыс. руб.
Ответ: Ставка процентов по кредиту с учетом инфляции = 0,3851(38,51%)
Погашаемая сумма = 236 648 тыс.руб.
Сумма начисленных процентов = 86 648 тыс.руб.
При учете векселя на сумму 25 тыс. руб., до срока оплаты которого осталось 90 дней, банк выплатил его предъявителю 22.5 тыс. руб.
Определите учетную ставку, которую использовал банк, если расчетное число дней в году равно 360.
Определим учетную ставку, которую использовал банк по следующей формуле:
d – учетная ставка в относительных единицах;
S – сумма по векселю;
t – количество дней от даты учета до даты погашения векселя;
Р – cумма, полученная предъявителем векселя;
К – число дней в году.
Подставим значения в формулу:
Ответ: Учетная ставка, которую использовал банк = 39,99%.
Вклад в сумме 3000 руб. размещен в банке на полгода с ежемесячным начислением сложных процентов по ставке 8% годовых.
Определите доход вкладчика по окончании срока договора.
Определим доход вкладчика по окончании срока договора следующим образом:
Количество периодов начисления равно:
Следовательно, накопленная сумма составит:
S=3 000·(1+) 6 = 3 184,6 руб.
Доход вкладчика по окончании срока договора будет равен:
I = 3 184,6 – 3 000 = 184,6 руб.
Ответ: Доход вкладчика по окончании срока договора = 184,6 руб.
Банк принимает депозиты на три месяца по ставке 4% годовых, на 9 месяцев по ставке 7.5% годовых и на год по ставке 9% годовых. Определите сумму, которую получит владелец депозита 50 тыс. руб. во всех трех случаях.
Определим сумму, которую получит владелец депозита во всех 3-х случаях.
Сумма депозита с начисленными процентами будет равна:
S=50 000·(1+0,04) 3 =56 243,2 руб.
Сумму, которую получит владелец депозита, составит:
I=S-P=56 243,2-50 000=6 243,2 руб.
Сумма депозита с начисленными процентами будет равна:
S=50 000·(1+0,075) 9 =95 861,9 руб.
Сумму, которую получит владелец депозита, составит:
I=S-P=95 861,9-50 000=45 861,9 руб.
Сумма депозита с начисленными процентами будет равна:
S=50 000·(1+0,09) 12 =140 633,2 руб.
Сумму, которую получит владелец депозита, составит:
I=S-P=140 633,2-50 000=90 633,2 руб.
Ответ: Сумму, которую получит владелец депозита:
В 1-ом случае = 6 243,2 руб.
Во 2-ом случае = 45 861,9 руб.
Вексель на сумму 10 тыс. руб. предъявлен в банк для оплаты за 100 дней до срока его погашения. Банк для определения своего дохода использовал ставку простых процентов в размере 20% годовых.
Определите сумму, выплаченную предъявителю векселя, и сумму дисконта банка для расчетного количества дней в году, равного 365.
Определим сумму дисконта банка для расчетного количества дней в году, равного 365:
где D – сумма дисконта;
Т – срок от даты учета векселя до даты погашения;
В – вексельная сумма;
I – учетная ставка банка.
Подставим значения в формулу:
Сумму, выплаченную предъявителю векселя найдем по формуле:
Подставим значения в формулу:
В / = 10 000 тыс.руб. – 547,9 руб. = 9 452,1 тыс.руб.
Ответ: Сумма, выплаченная предъявителю векселя = 9 452,1 тыс. руб.;
Сумма дисконта банка = 547,9руб.
Список использованной литературы
1. Капитоненко В.В. Задачи и тесты по финансовой математике: учеб. пособие. – М.: Финансы и статистика, 2007. – 256 с.
2. Кузнецов Б.Т. Финансовая математика: Учебное пособие для вузов / Б.Т. Кузнецов. – М.: Издательство «Экзамен», 2005. – 128 с.
3. Коптева Н.В., Семенов С.П. Финансовая математика. / Сервер электронных публикаций ММЦ АлтГУ, 2003.
4. Организационные особенности инвестиционной деятельности российских коммерческих банков//Банковское дело. – 1994. – №7.
5. Положение об инвестиционном конкурсе по продаже пакетов акций акционерных обществ, созданных в порядке приватизации государственных и муниципальных предприятий //Экономика и жизнь. – 1994. – № 12.
6. Черкасов В.Е., Плотицына Л.А. Банковские операции: маркетинг, анализ, расчеты. – М.: Метаинформ, 1995.
Источник
Простая процентная ставка с учетом инфляции.
При использовании простых процентов применяется формула:
 |
S — наращенная сумма без учета инфляции;
Sa — наращенная сумма с учетом инфляции (уровень a);
P — первоначальная сумма;
n — срок кредита в годах;
i — простая процентная ставка без учета инфляции (реальная доходность);
ia — простая процентная ставка с учетом инфляции.

|
 | (4.1) |
Пример 4.2. Кредит 50000 рублей выдан на 6 месяцев. Какова должна быть простая процентная ставка, если кредитор желает получить 10% реальной доходности, начисляемых по простой процентной ставке при уровне инфляции 20% в год? Вычислить наращенную сумму.
| Дано: | Решение: |
 n = 0,5 лет P = 50000 руб. α = 20% = 0,20 i = 10% = 0,10 n = 0,5 лет P = 50000 руб. α = 20% = 0,20 i = 10% = 0,10 | |
| ia = ? Sa = ? | Ответ: 57750 рублей. |
Существуют задачи и другого типа, связанные с инфляцией.
Пример 4.3. Кредит выдан на 2 года под 30% годовых, начисляемых по простой процентной ставке. Оценить реальную доходность данной финансовой операции с точки зрения кредитора. Уровень инфляции равен 25% в год.
| Дано: | Решение: |
 n = 2 года α = 25% = 0,25 ia = 30% = 0,30 n = 2 года α = 25% = 0,25 ia = 30% = 0,30 | |
| i = ? | Ответ: реальная доходность 1,2% годовых, начисляемых по простой процентной ставке. |
Простая учетная ставка с учетом инфляции.
 |
Формула для простой учетной ставки следующая:
|
 |
Учесть инфляцию можно двумя способами:
 |
Пример 4.4. Под какую простую учетную ставку нужно выдать кредит на 6 месяцев, чтобы реальность доходность операции составила 10% при уровне инфляции 20% в год?
Пример 4.5. Ссуда дана по учетной ставке 30% годовых на 6 месяцев. Какова реальная доходность операции с точки зрения кредитора при уровне инфляции 25%?
Сложная процентная ставка с учетом инфляции. Пример 4.6. Кредит в размере 40000 рублей выдан на два года. Реальная доходность должна составить 10% годовых, начисляемых ежеквартально. Ожидаемый уровень инфляции 20% в год. Определить сложную ставку процентов кредита, компенсирующую инфляционные потери, и вычислить наращенную сумму.
Пример 4.7. Определите реальную доходность финансовой операции, если при уровне инфляции 20% в год кредит выдается на 2 года по номинальной ставке сложных процентов в размере 30% годовых при ежеквартальном начислении процентов.
Пример 4.8. Определить, какой реальной доходностью обладает финансовая операция, если при уровне инфляции 20% в год деньги вкладываются на 2 года под 15% годовых при ежемесячном начислении процентов. Источник |



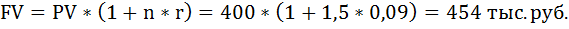
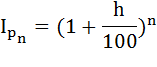
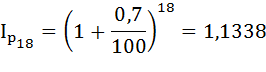
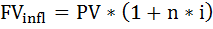
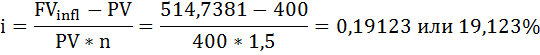
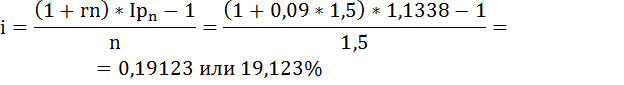

 n = 0,5 лет α = 20% = 0,20 d = 10% = 0,10
n = 0,5 лет α = 20% = 0,20 d = 10% = 0,10 n = 0,5 лет α = 25% = 0,25 da = 30% = 0,30
n = 0,5 лет α = 25% = 0,25 da = 30% = 0,30 P = 40000 руб.
P = 40000 руб. n = 2 года jα = 30% = 0,30 a = 20% = 0,20 m = 4
n = 2 года jα = 30% = 0,30 a = 20% = 0,20 m = 4