Доходность кредитов с учетом удержания комиссионных
Эффективная процентная ставка по кредиту — это ставка, которая учитывает все расходы заемщика, связанные с оформлением, получением и обслуживанием кредита.
При расчете эффективной ставки учитываются все дополнительные расходы заемщика, связанные с получением и обслуживанием кредита, такие как:
¾ проценты по ссуде, которые должен уплатить заемщик;
¾ комиссии и иные сборы банка, которые должен уплатить заемщик за пользование кредитом:
¾ комиссия за рассмотрение кредитной заявки (оформление кредита);
¾ комиссия за выдачу и сопровождение кредита;
¾ комиссии за открытие, ведение (обслуживание) ссудного (текущего) счета (за расчетное и операционное обслуживание);
¾ вытекающие из условий кредитного договора (дополнительных соглашений к договору) платежи в пользу третьих лиц, в том числе:
a. услуги нотариуса;
b. услуги по государственной регистрации и (или) оценке передаваемого в залог имущества (квартиры);
c. услуги по страхованию жизни заемщика, кредита, предмета залога (квартиры, автомобиля), права собственности владельца квартиры и любые иные платежи — в части, прямо или косвенно перечисляемой этими третьими лицами в пользу банка.
За счет учета дополнительных расходов заемщика, связанных с получением и обслуживанием кредита, значение эффективной ставки может получиться заметно больше указанной в договоре.
Эффективная ставка простых процентов по кредиту с учетом удержания комиссионных будет равна:

где g — срок кредита в днях;
K — расчетное количество дней в году (360);
i — номинальная процентная ставка по кредиту;
G — доля комиссионных в относительных единицах.
Если кредит выдается по ставке сложных процентов g на n лет, значение эффективной ставки сложных процентов по кредиту с учетом удержания комиссионных будет равна:

где n — срок кредита в годах.
В нашем случае эффективная ставка процентов по кредиту с учетом удержания комиссионных, согласно формуле 26, будет равна:
где 0,02 — доля комиссионных в относительных единицах.
Учитывая все вышеизложенные затраты клиента на получение и пользование кредитом, эффективная процентная ставка (ЭПС) получается выше процентной ставки, указанной в кредитном договоре.
Эффективная процентная ставка — это стандартная, широко используемая кредитными организациями расчетная величина. Она предназначена для того, чтобы проинформировать заемщиков и помочь им в сравнении и выборе различных условий кредитования. Для вычисления эффективной ставки сначала подсчитывается суммарный долг (размер кредита с учетом всех комиссий и страховых платежей), далее рассчитывается условный ежемесячный платеж, который определяется исходя из предположения, что банк выдает сумму рассчитанного суммарного долга под указанные им проценты и на указанный срок.
Источник
ДОХОДНОСТЬ УДЕРЖАНИЯ КОМИССИОННЫ
Рассмотрим несколько случаев расчета доходности при удержании банком комиссионных.
Случай 1. Пусть при выдаче ссуды по простой ставке процентов сроком на п лет с суммы ссуды удерживаются комиссионные.
Р(1 + п X inp ) = (Р — ДР)(1 + п X пр),
где ДР — увеличение первоначальной суммы, связанное с комиссионными; ізпр — эффективная ставка простых процентов.
Величина комиссионных ДР = h х Р, где h — доля комиссионных в размере ссуды (десятичная дробь). Отсюда
Р(1 + п X із пр ) = Р(1 — Д)(1 + п X із пр).
Из этого уравнения получаем выражение для эффективной ставки простых процентов, определяющей доходность финансовой операции:
Случай 2. Если для расчета доходности операции по выдаче ссуды по простой ставке процентов сроком на га лет и удержания с суммы ссуды комиссионных используется ставка сложных процентов, то уравнение эквивалентности наращенной сумме будет иметь вид:
Р(1 + гаіпр) = (Р-ДР)(1 + ізол)»
Р(1 + га х іпр) = Р(1 — Л)(1 + ?Э J» .
Из этого уравнения можно рассчитать доходность операции по выдаче кредита по простым процентам с учетом комиссионных, измеряемую в виде эффективной ставки сложных процентов:
і = дА ; L — 1. (4.25)
Случай 3. Если при выдаче кредита используются сложные проценты (q), то уравнение эквивалентности с выплатой комиссионных будет иметь вид:
Р( 1 + в)» =P(l-ft)(l-Неэффективную ставку сложных процентов можно рассчитать следующим образом:
где nd = д / Kd ; Щ =Э / Ki — периоды операции по учету векселей. Выражение для эффективной ставки сложных процентов с удержанием комиссионных имеет вид:
Случай 5. Если для измерения эффективности удержания комиссионных при операции учета используется эффективная ставка простых процентов, то уравнение эквивалентности будет иметь вид:
Отсюда получаем выражение для эффективной ставки простых процентов с удержанием комиссионных:
(1 — d/Kd х d)( 1 — h)
Рассмотрим примеры расчетов финансовых операций с удержанием комиссионных.
Пример 57. При выдаче кредита под 40% годовых удерживаются комиссионные в размере 1% суммы ссуды. Определите доходность финансовой операции для срока ссуды 180 дней (Я = 360) при использовании ставок простых и сложных процентов. Сравните полученный результат с доходностью без выплаты комиссионных. Сделайте выводы.
1. Доходность операции в виде эффективной ставки простых процентов определим по формуле (4.23):
(180 / 360) • 0,4 + 0,01 _ 0,21
(180 / 360)(1 — 0,01) 0,495
2. Доходность операции в виде ставки сложных процентов определим по формуле (4.25):
+ (180/360) 0,4 1 — 0,01
- Без выплаты комиссионных эффективная ставка сложных процентов в соответствии с формулой (4.7) будет равна
К.щ, = 180/36^1 + (180 /360) • 0,4 — 1 = 0,44 (44%).
- Изменение доходности операции за счет выплаты комиссионных составит:
Лі, = 46,9 — 44 = 2,9%.
Таким образом, доходность операции по выдаче ссуды с выплатой комиссионных будет выше в связи с тем, что при удержании комиссионных сумма фактически выданной ссуды уменьшается.’
Пример 58. Определите изменения доходности финансовой операции банка за счет удержания комиссионных из расчета 2% суммы ссуды под сложные проценты (55 и 75%), если известно, что ссуда выдана на 4 года.
Случай 1. Ставка сложных процентов составляет 55%. Эффективная ставка сложных процентов [см. формулу (4.26)]
Увеличение эффективности ссудной операции составит
Лі, = 1эсл — q — 0,558 — 0,55 = 0,008 (0,8%). Случай 2. При ставке сложных процентов 75%
Увеличение эффективности ссудной операции составит:
Ч “ *..« — ч = °’759 — °-75 = 0.009 (0,9%).
Как видим, эффективность ссудной операции за счет удержания комиссионных возрастает в зависимости от роста ставок сложных процентов.
Пример 59. Обязательство учтено в банке по ставке 50% за 183 дня до его оплаты. При учете векселя с его владельца удержаны комиссионные в размере 1,5%. Определите доходность операции, рассчитанную по эффективным ставкам простых и сложных процентов при К, — 366 и Kd = 360 дней. Рассчитайте изменение в доходности операций с удержанием и без удержания комиссионных.
4 Л.Г. Батракова
- Доходность операции с удержанием комиссионных при эффективной ставке сложных процентов [см. формулу (4.28)]
\ (1 -183/360 0,5)(1-0,015)
- Доходность без удержания комиссиониых операции при эффективной ставке сложных процентов [см. формулу (4.7)]
^ -1- — у 1 — 183 / 366 • 0,5
- Увеличение доходности операции за счет удержания комиссионных при ставке сложных процентов составит
М = і — і* = 0,851 — 0,778 = 0,073 (7,3%).
3 ,СЛ Э.СЛ а ‘ ‘ 4 ‘
- Доходность операции с удержанием комиссионных при эффективной ставке простых процентов [см. формулу (4.30)]
(1 — 183 / 360 • 0,б)(1 — 0,015)
- Доходность операции без удержания комиссионных при эффективной ставке простых процентов [см. формулу (4.3)]
1э.пр “ 360 _ 18g _ 0 g
- Увеличение доходности операции за счет удержания комиссионных при ставке простых процентов составит
Источник
Доходность ссудных и учетных операций с удержанием комиссионных
Ссудные операции. Доходность ссудных операций (без учета комиссионных) измеряется с помощью эквивалентной годовой ставки сложных процентов (см. параграф 3.3). За открытие кредита, учет векселей и другие операции кредитор часто взимает комиссионные, которые заметно повышают доходность операций, так как сумма фактически выданной ссуды сокращается.
Пусть ссуда в размере D выдана на срок n. При ее выдаче удерживаются комиссионные за операцию (G). Фактически выданная ссуда равна D — G. Пусть для начала сделка предусматривает начисление простых процентов по ставке i. При определении доходности этой операции в виде годовой ставки сложных процентов iЭ исходим из того, что наращение величины D — G по этой ставке должно дать тот же результат, что и наращение D по ставке i. Разумеется, уменьшение фактической суммы кредита связано не только с удержанием комиссионных. Однако для краткости любое удержание денег, сделанное в пользу кредитора, будем называть в этой главе комиссионными.
По определению балансовое уравнение запишем в виде:
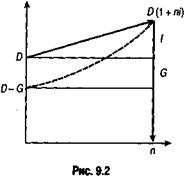
Графическое изображение данной сделки (контур) показано на рис. 9.2. Пусть G = D(1 — g), где g — относительная величина комиссионных в сумме кредита, тогда
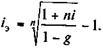
Полученный показатель доходности можно интерпретировать как скорректированную цену кредита.
При расчете iЭ будем полагать, что временная база всегда 365 дней. При начислении процентов на сумму ссуды полагаем, что K = 360 или 365 дней.
Ставка iЭ не фигурирует в условиях операции, она полностью определяется ставкой процентов и относительной величиной комиссионныхпри заданном сроке сделки.
Предположим, что необходимо охарактеризовать доходность в виде ставки простыхпроцентов (iЭП). В этом случае на основе соответствующего балансового уравнения находим
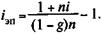
Пример 9.1.При выдаче ссуды на 180 дней под 8% годовых кредитором удержаны комиссионные в размере 0,5% суммы кредита. Какова эффективность ссудной операции в виде годовой ставки сложных процентов? Пусть при начислении процентов K = 365, тогда по формуле (9.2) находим
iЭ = 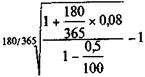
Если ссуда выдается под сложные проценты, то исходное уравнение для определения iЭ имеет вид
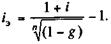
Пример 9.2. В какой мере удержание комиссионных из расчета 1 % суммы кредита увеличивает эффективность ссуды для кредитора при пяти- и десятилетнем сроке?
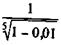
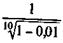
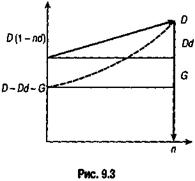
Учетные операции. Если доход извлекается из операции учета по простой учетной ставке, то эффективность сделки без удержания комиссионных определяется по формуле эквивалентной ставки (3.20). При удержании комиссионных и дисконта заемщик получает сумму D — Dd — G. Если дисконт определяется по ставке простых процентов, то эта сумма составит D(1- nd — g). Контур операции показан на рис. 9.3. Балансовое уравнение в данном случае имеет вид
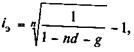
где n — срок, определяемый при учете долгового обязательства.
Для полного показателя доходности в виде iэп находим
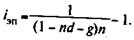
Временная база при расчете iЭ принимается равной 365 дням, в учетной операции — 360 или 365 дням (подробнее см. параграфы 1.3 и 1.6).
Пример 9.3. Вексель учтен по ставке d = 10% за 160 дней до его оплаты. При выполнении операции учета с владельца векселя удержаны комиссионные в размере 0,5%. Доходность операции согласно (9.5) при условии, что временная база учета 360 дней, составит
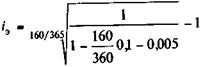
Эффективность без удержания комиссионных — 10,8%.
Во всех рассмотренных случаях искомая ставка iЭ представляет собой частный случай упомянутой выше ПД. Заметим, что влияние комиссионных на iЭ уменьшается по мере увеличения срока сделки.
Удержание комиссионных — не единственная возможность изменения фактической суммы инвестиций по сравнению с номиналом. В практике возможны случаи, когда инвестор несет дополнительные расходы, например приобретая опцион на право купить ценную бумагу. Такие расходы, очевидно, формально можно рассматривать как комиссионные с обратным знаком (-G)и для расчета применять полученные выше формулы (9.2) — (9.6).
Пример 9.4. Всероссийский биржевой банк выпустил в обращение депозитный сертификат (в виде монеты) достоинством 5 тыс. руб. с условиями: продажа по нумизматической стоимости, цена опциона на право покупки 50 руб.; сертификаты принимаются к оплате ВББ по номиналу до 30 декабря 1996 г. и по двойному номиналу через 5 лет, т.е. с 31 декабря 1996 г.
Поставим перед собой задачу определить доходность инвестиций в такой сертификат без учета нумизматической ценности монеты. Инвестор, как было показано, несет дополнительные расходы по приобретению опциона, т.е. G = -50 и, следовательно, g = -50/5000 = -0,01. Учтем также, что в первые пять лет i = 0. Если допустить, что монета будет реализована в качестве платежного средства в ВББ через четыре года после ее выпуска,то получим
iЭ = 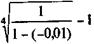
При наступлении права получить двойной номинал имеем 1 + + 5i = 2, отсюда
iЭ = 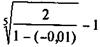
При рассмотрении рисунков 9.2, 9.3 становится очевидным, что контур финансовой операции, основанный на договорной ставке i, может быть дополнен контуром по ставке iЭ. Это позволяет лучше понять сущность ПД, по крайней мере в рамках рассмотренных простых сделок. Кроме того, становится очевидным вклад комиссионных в общий доходпо сделке.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник