Доходность к погашению (Yield to Maturity, YTM)
По сути доходность к погашению является внутренней нормой доходности (англ. Internal Rate of Return) для инвестора, который купил облигацию по рыночной цене и намеревается удерживать ее вплоть до даты погашения (англ. Maturity Date). Другими словами, она является ставкой дисконтирования, использование которой позволит привести все купонные платежи и номинальную стоимость облигации к ее настоящей стоимости (рыночной цене) сегодня. Таким образом, найти доходность к погашению можно решив следующее уравнение.
где P – рыночная стоимость (цена приобретения) облигации;
n – количество купонных платежей при условии, что облигация будет удерживаться до даты погашения;
C – размер купонного платежа;
F – номинальная стоимость облигации;
r – доходность к погашению.
Используя эту формулу необходимо учитывать периодичность осуществления купонных платежей, что определяется условиями эмиссии. Как правило, эти платежи осуществляются каждые полгода, гораздо реже ежегодно или ежеквартально. Поэтому полученную доходность к погашению иногда необходимо скорректировать к годовому выражению. Чтобы лучше разобраться в ситуации рассмотрим ее на примере.
Пример. Инвестор приобрел 5-ти летнюю облигацию за 4875 у.е. При этом ее номинальная стоимость составляет 5000 у.е., а купонная ставка 14% годовых, при условии что купонные платежи осуществляются каждые полгода. Чтобы использовать приведенное выше уравнение нам необходимо рассчитать размер и количество купонных платежей. Поскольку выплаты осуществляются два раза в год, а срок обращения облигации составляет 5 лет, то количество купонных платежей будет равно 10 (5*2). Купонная ставка в 14% годовых предполагает, что эмитент облигации должен ежегодно выплачивать инвестору 700 у.е. (5000*0,14). Однако учитывая тот факт, что выплаты осуществляются два раза в год, размер купонного платежа составит 350 у.е. Таким образом, мы можем подставить полученные данные в уравнение и рассчитать доходность к погашению.
Для решения этого уравнения можно воспользоваться различными финансовыми калькуляторами или использовать функцию «ВСД» Microsoft Excel, для чего исходные данные необходимо представить следующим образом.
Затраты на приобретение облигации, осуществленные в 0-вой точке, необходимо записать в ячейку со знаком «-». По истечении 5-ти лет вместе с последним купонным платежом инвестор получит номинальную стоимость облигации, поэтому в последнюю ячейку необходимо занести их сумму 5350 у.е. (5000+350). В результате мы получим доходность к погашения, равную 7,362%.
Следует отметить, что полученная доходность к погашению выражена в полугодичном выражении. Поэтому чтобы представить ее в годовом выражении необходимо скорректировать ее с учетом сложных процентов. Для условий нашего примера она составит 15.266%.
Существует определенная зависимость между ценой облигации и ее доходностью к погашению.
1. Если доходность к погашению равна купонной ставке, то облигация торгуется по номинальной стоимости.
2. Если доходность к погашению меньше купонной ставки, то рыночная стоимость облигации будет выше номинала, то есть она будет торговаться с премией.
3. Если доходность к погашению больше купонной ставки, то рыночная стоимость облигации будет ниже номинала, то есть она будет торговаться с дисконтом.
Давайте проиллюстрируем эти закономерности на основе данных приведенного выше примера.
Действительно, если облигация будет приобретена за 5000 у.е., то есть за номинальную стоимость, то доходность к погашению будет равна купонной ставке. Если рыночная стоимость облигации будет ниже 5000 у.е., то доходность к погашению будет превышать купонную ставку, и наоборот.
Ограничения в использовании
Доходность к погашению обладает тем же самым недостатком, как и внутренняя норма доходности. Изначально предполагается, что все полученные купонные платежи реинвестируются по ставке равной доходности к погашению, что крайне редко встречается на практике. Другими словами, если купонные платежи будут реинвестироваться по более низкой ставке, то доходность к погашению будет завышенной, а если по более высокой – то заниженной. Учитывая, что ситуация на рынке капиталов постоянно меняется, что приводит к постоянному изменению процентных ставок, полученные результаты расчетов могут использоваться только в течение непродолжительного периода времени.
Источник
Доходность к погашению (Yield to maturity, YTM)
Давно хотел понять, что такое доходность к погашению, но всё никак руки не доходили. Одно дело, когда тебе квик/сайт ММВБ показывает какое-то число, типа 5.25%, и вроде оно и должно быть правильным, но что за этим сто и т? И что это означает на практике? В инете есть сложные формулы доходности, и (если сможешь разобраться) они вроде считают приблизительно то же самое, но, опять же, почему они именно такие, как они получены? Хочется, чтобы этот процент, какой бы он ни был, можно было напрямую сравнивать со ставками банковских вкладов, потому что это просто и понятно.
Зачем нужно уметь считать доходность самому?
- Чтобы проверить, что она на самом деле такая.
- Чтобы учесть налог на купон для корпоративных бумаг, т.к. в квике он не учитывается.
- Чтобы учесть комиссию.
- Чтобы посчитать доходность для бумаг, по к-м нет торгов на бирже (есть на внебирже) и поэтому в квике показывается 0.
- Можно посчитать для любой цены или даты.
Сразу скажу, что самый простой способ посчитать доходность – это использовать функцию ДОХОД в Excel. Для примера я буду использовать еврооблигацию GAZPR-34 на 10.01.18 с ценой 137.5 и НКД 17,7292. В данном случае ф-я ДОХОД получает 4,284% (тут учитывается налог), но при этом она требует очень мало параметров:
ДОХОД(дата покупки; дата погашения; ставка купона; цена;100; 2; 0)*100.
НКД она считает сама. Есть и отдельная функция для подсчета НКД — НАКОПДОХОД(). Кроме того, в Excel есть и другие функции, к-е могут оказаться полезными:
ДАТАКУПОНДО/ДАТАКУПОНПОСЛЕ – определяют дату предыдущего/следующего купона
ЧИСЛКУПОН — число оставшихся купонов.
Сначала я (наверное, как и многие) предполагал, что тут весь фокус в капитализации и реинвестировании купонов, и даже стал считать таким образом доходность в Excel. Цифры получались близкие к тем, что показывал квик, но всё же не те, тем более, что по некоторым бумагам они отличались значительно.
Затем я придумал интервальный способ подсчета, в котором весь период времени до погашения разбивается на интервалы длиной полгода (между купонами), и доходность считается для каждого из них, а затем получается средневзвешенная дох-ть для всего периода. Здесь делается предположение, что цена с момента покупки до погашения равномерно снижается (или увеличивается) до номинала. Зная количество дней до погашения и текущую цену, можно получить предполагаемое изменение цены за 1 день, и за любое число дней, а значит – и в день выплаты каждого купона. А зная последние, можно для каждого интервала получить:
- Сумма вначале (цена)
- Сумма в конце (цена в конце + купон)
- Разница, процент и годовой процент
Для самого 1-го периода ситуация несколько усложняется НКД, но это не принципиально. Далее, получив для каждого интервала годовой процент и зная цену в его начале, можно получить средневзвешенный годовой процент за всё время (используя цену как вес т.к. она всё время меняется). Полученное значение уже больше похоже на то что показывает квик, но и оно немного отличается. Проблема в том, что оно начинает заметно меняться, когда от даты покупки до первого купона остается мало времени, особенно, если учесть комиссию. Причина оказывается в том, что т.к. длина интервала в днях тоже разная её тоже надо учитывать как вес. При добавлении её в расчеты результат перестает зависеть от длины первого интервала. В Excel всё это выглядит примерно так (здесь не учитывается НДФЛ):
Проблема с этим способом состоит в том, что он основан на предположении, что цена идет к номиналу равномерно, а в реальности это не так, и в идеале определение доходности от цены зависеть не должно.
В какой-то момент попался пост на эту тему anatolyutkin «Еврооблигации и депозиты», к-й дал подсказку. На самом деле там всё написано, но т.к. у меня в финансовой области образования нет, то я его сразу осилить не смог, тем более что там в расчётах используется Бином Ньютона и т.п., но всё же я понял основную идею – текущая стоимость. Оказывается, это такой финансовый термин, к-й означает сколько нужно вложить сегодня, чтобы через какое-то время получить заданную сумму. Фокус в том, что обычно расчет производится наоборот – имеем сумму, например 1000р, процент (8%), и через год получаем 1080р. А здесь известно, сколько будет в конце и процент, а найти надо, сколько было вначале.
Ну а дальше основной финт мозгами состоит в том, чтобы понять, что когда вы покупаете облигацию (затраты = текущая цена + НКД), вы как бы открываете много маленьких вкладов на разные сроки. Вкладов столько, сколько вы получите купонов + еще 1 для номинала. Каждый вклад закрывается, когда вы получаете по нему купон, и все вклады имеют одинаковый процент.
Но здесь есть 1 нюанс – считать нужно так, как будто эти вклады имеют капитализацию. Её на самом деле конечно нет, но это нужно делать для того, чтобы полученный процент соответствовал каким-то общепринятым ориентирам. Если нам нужно сравнить доходность с обычными вкладами, то можно использовать годовую капитализацию. С другой стороны,
In a number of major markets (such as gilts) the convention is to quote annualised yields with semi-annual compounding
Что означает, что существует соглашение указывать доходность с полугодичной капитализацией, так что можно посчитать и так. Понятно, что из-за более частой капитализации процент доходности будет немного ниже. В квике, на сайте ММВБ и в функции ДОХОД доходность вычисляется именно так. Формула для расчета начальной суммы отдельного вклада для годовой капитализации выглядит так:
Sum=EndSum / ((1+Rate/100)^Years) / (1+Rate/100*YearPart)
Здесь EndSum – купон или номинал, Rate – искомый процент, Years — число полных лет вклада, YearPart – дробная часть лет. Для полугодичного варианта:
Sum=EndSum / ((1+Rate/200)^YearHalves) / (1+Rate/100* YearHalfPart)
Здесь YearHalves – число полных полугодий, YearHalfPart — дробная часть полугодий. Далее, если просуммировать все начальные суммы этих вкладов, то должно получиться число, равное первоначальным затратам, т.е. текущая цена + НКД. Другими словами, тут нельзя получить формулу типа Rate=… где доходность вычисляется одним выражением – нужно подбирать разные значения до тех пор, пока результат не будет отличаться от требуемого на величину типа 0.00001. В Excel это выглядит так (здесь НДФЛ уже учтен, при этом для простоты в НКД он тоже учтён): 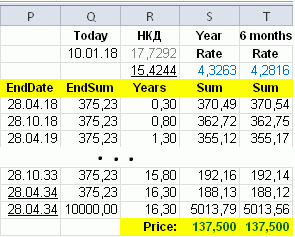
Конечно, так рассчитывать доходность не нужно, это просто для понимания. В интернете также можно найти более простые формулы для расчета доходности без суммирования, в к-х присутствует параметр «общее количество купонных платежей», но при этом не учитывается НКД. Кроме того, на сайте ММВБ есть документ «Методика расчета НКД и доходности» , содержащий формулу доходности с параметром «число дней». Этот параметр делится на число дней в году, т.е. получается число лет, т.о., данная формула получает доходность с годовой капитализацией, и это не та величина, к-я показывается на этом же сайте для конкретных бумаг .
Еще раз скажу про заблуждение насчет реинвестирования – оно в расчете ДП не учитывается:
A common misconception is that the coupons must be reinvested at the yield to maturity… making this assumption is a common mistake in financial literature and coupon reinvestment is not required for YTM formula to hold.
(Вики)
It is a chronic error in that it persists in spite of continued attempts to correct it. For example, Renshaw addressed this error fifty years ago … but the reinvestment assumption continues to be replicated. … successive generations of financial professionals educated with the erroneous text have restated the claim in materials intended to educate investors….
Among the sites containing this claim are Bloomberg.com,… Investopedia.com, Morningstar.com, and even the popularly edited Wikipedia.org…
(«Yield-to-Maturity and the Reinvestment of Coupon Payments»)
Получаемая величина ДП, например 4.3%, означает только процент, к-й начисляется на вложенные средства только пока вы владеете данной ЦБ. Как только вы получили деньги (купон) назад, этот процент начисляться перестает а его новые инвестиции к нему никакого отношения не имеют. Разница только в том, что в случае обычного вклада вы получаете сразу всю сумму назад с процентами, а здесь как бы есть много маленьких вкладов под одинаковый процент и вы получаете их по одному постепенно.
Т.к. нам более привычна ситуация когда вся сумма возвращается сразу, можно попытаться посчитать и т.н. реальную доходность с учетом последующего (ре)инвестирования купонов (необязательно в ту же ЦБ) до погашения. Для каждого купона срок его реинвестирования равен
где EndDate – дата погашения и CouponDate – дата выплаты купона. Сумма, к-я получается в результате реинвестирования купона рассчитывается по формуле:
ReinvSum = Coupon * ((1+ReinvRate/100)^ReinvYears) * (1+ReinvRate/100*ReinvYearPart)
(здесь подразумевается ежегодная капитализация). Если просуммировать все такие суммы, а также последний купон и номинал, то получится итоговая сумма за весь срок до погашения. Зная начальную (Sum1=цена + НКД) и конечную сумму EndSum, а также срок, можно подобрать ставку, к-я даст такой результат, используя ту же формулу:
EndSum = Sum1 * ((1+RealRate/100)^TotalYears) * (1+RealRate/100*TotalYearPart)
Очевидно, что на практике реинвестировать под ту же ставку не получится, поэтому можно просто рассмотреть разные варианты для оценки. Для того же примера с ДП = 4,3263%:
- Если ReinvRate=0 (купоны вообще не инвестируются), то RealRate=2,96%
- Если ReinvRate=3%, то RealRate=3,876%
- Если ReinvRate=Rate=4,3263%, то реальная дох-ть будет такой же
- Если ReinvRate=5%, то RealRate=4,567%
Как видим, ставка реинвестирования влияет на итоговую реальную доходность.
Источник