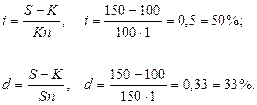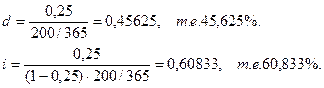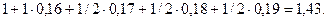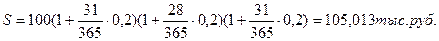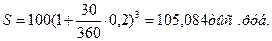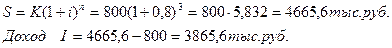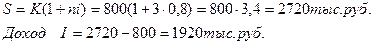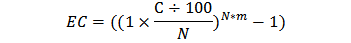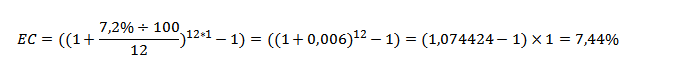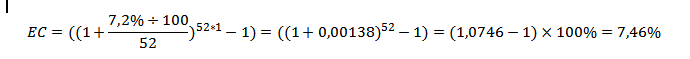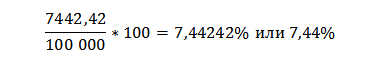Доходность операции с эффективной учетной ставкой

Формулы доходности финансовых операций

Если в формулах наращения по процентной и учетной ставке принять срок n = 1 году, то получим, что

.

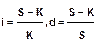
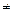
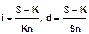
Если n1 году, .

Эти формулы принято называть формулами доходности или эффективности по простой ставке процентов и учетной ставке соответственно.

Предприятие получило кредит на 1 год в размере 100 млн. с условием возврата 150 млн.

Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок.

К = 100 млн., S = 150 млн., n = 1 год. I = ?, d = ?

Решение:

Дисконтная ставка всегда меньше процентной, ибо она учитывает время более жестко.

Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли (или процента) от суммы погасительного платежа. Таким образом, уровень процентной ставки задается в неявном виде. Выведем формулы, с помощью которых можно вычислить значения этих ставок.

Пусть S- размер погасительного платежа (сумма ссуды к концу срока),

d_n – доля этого платежа, определяющая величину дисконта за весь срок ссуды.

К = S(1 – d_n) – реально выдаваемая ссуда в момент заключения договора.

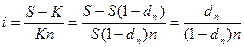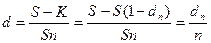Задача 7.

Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней.

Простые переменные ставки

В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.

Если i₁, i₂,… i_k – последовательные во времени простые ставки,

а n_1, n_2,… n_k – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:

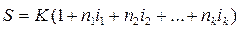Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.

Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года.

Множитель наращения =

Иначе, за 2,5 года начальный капитал увеличился в 1,43 раза.

Реинвестирование

В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!)

В этом случае наращенная сумма для всего срока составит:

(14) k – количество реинвестиций.

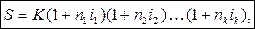
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:

, k – количество реинвестиций.

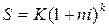
Задача 9.

Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам.

По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам.

По точным процентам:

(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!)

По банковским процентам при условии, что в каждом месяце по 30 дней:

Модуль 2. Сложные проценты

Наращение по сложным процентам

В среднесрочных и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты.

Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов.

Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид

(1) , где i — годовая (номинальная) процентная ставка, n — число лет начисления,

— множитель наращения по сложным процентам.

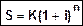
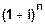
Задача 1.

Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

2. Простые проценты:

За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам.

Задача 2.

Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

Источник

Эффективная ставка по вкладу

Банковские депозиты являются одним из инструментов инвестирования, который приносит гарантированный доход. Они являются самыми низкорисковыми и пассивными, поскольку не требуют вмешательства клиента, а получением прибыли занимается профессиональный участник – финансовая организация. Зачастую, рекламируется для клиентов ставка по вкладу, которая является номинальной, что в сути не отражает реальной прибыли. Эффективная ставка же по вкладу отражает реальную прибыльность вклада. Рассмотрим что это такое более подробнее.

Что такое эффективная ставка по вкладу?

Чтобы оценить настоящий доход, который можно получить от вложения своих денег на депозит, используется эффективная ставка. Она отражает прибыль клиента с учетом капитализации процентов во вклад и всегда будет выше номинальной ставки. Как показывает практика, доход от вклада с капитализацией имеет бОльшую прибыльность, чем вклад без капитализации.

Это происходит из-за того, что проценты при капитализации начисляются с выбранной периодичностью (в месяц, в квартал, в полугодие, в год) и суммируются к основному телу депозита.

Зачем нужна эффективная ставка по вкладу, и чем она полезна для клиента?

Она отражает общий доход за весь срок с учетом причисления процентов к вкладу. Это помогает клиенту оценить его реальный доход и сравнить условия по видам депозитов в одном или нескольких банках. Если владелец депозита желает получить максимальный доход, то ему следует выбирать вклады с ежемесячной капитализацией процентов.

Как это работает? В первый месяц проценты начисляются на сумму вклада и присоединяются к нему. Во второй месяц проценты начисляются уже на сумму вклада+проценты за первый месяц. Следовательно, эта сумма уже будет больше, чем в первый месяц и т.д. В этом случае используется формула сложного процента, т.е. когда идет начисление процентов на увеличивающуюся сумму. Итоговая доходность будет выше исходной процентной ставки.

Формула расчета эффективной ставки.

Чтобы посмотреть наглядно, как идет начисление, нужно воспользоваться формулой расчета эффективного процента по депозиту:

1. ЕС – это эффективная ставка по вкладу, т.е. значение доходности, которое получится при причислении процентов к основному телу вклада за определенный срок
2. С – это номинальная ставка, т.е. то значение, которое обычно указывается в договоре
3. N – это количество периодов капитализации в год (если ежемесячная капитализация, то N=12, если еженедельная, то N=52, если ежеквартальная, то N=4)
4. m – это количество повторений периодов (если на один год, то m=1, если на два года, то m=2 и т.д).

Просчитаем эффективную ставку по вкладу Сбербанка «Управляй» на 100 000 на один год с ежемесячным причислением процентов с номинальной ставкой 7,2%. Ниже представлен ручной расчет, но можно воспользоваться калькулятором депозитов, просто вбив параметры своего вклада.

Если бы депозит открыт на год, а проценты начислялись каждую неделю, то формула выглядела бы следующим образом (берем N=52, т.к. в году 52 недели):

Таким образом, если расположить 100 000 рублей на один год с капитализацией процентов ежемесячно, то эфф.ставка составит 7,44%, что на 0,24% больше номинала. Если капитализация будет производиться еженедельно, то эфф.ставка за год составит 7,46%.

Чтобы проверить это значение на практике, произведем расчет на примере этого же вклада (с ежемесячной капитализацией). Используем формулу для расчета %-ов:

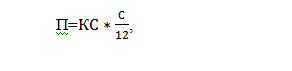
где

• П – сумма начисленных процентов за каждый месяц,
• КС – капитализированная сумма с учетом причисления процентов за предыдущий месяц,
• С – ставка номинальная.

Месяцы	Кап.сумма, руб	Ставка в месяц	Проценты за месяц, руб
1	100 000	0,006	600
2	100600	0,006	603,6
3	101203,6	0,006	607,22
4	101810,82	0,006	610,87
5	102421,69	0,006	614,53
6	103036,22	0,006	618,22
7	103654,43	0,006	621,93
8	104276,36	0,006	625,66
9	104902,02	0,006	629,41
10	105531,43	0,006	633,19
11	106164,62	0,006	636,99
12	106801,61	0,006	640,81
Итого	7442,42

Теперь рассчитаем эфф.ставку. Для этого разделим полученную сумму процентов на первоначальную сумму вклада:

Месяцы	Кап.сумма, руб	Ставка в месяц	Проценты за месяц, руб
1	100 000	0,006	600
2	100600	0,006	603,6
3	101203,6	0,006	607,22
4	101810,82	0,006	610,87
5	102421,69	0,006	614,53
6	103036,22	0,006	618,22
7	103654,43	0,006	621,93
8	104276,36	0,006	625,66
9	104902,02	0,006	629,41
10	105531,43	0,006	633,19
11	106164,62	0,006	636,99
12	106801,61	0,006	640,81
Итого	7442,42

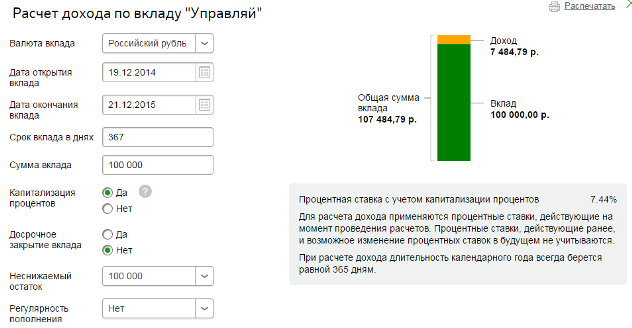
Произведем расчет на калькуляторе Сбербанка:

Как видно из рисунка, суммы практически совпадают. Небольшое различие в 42 рубля связано с тем, что 19.12.2015 г. попадает на выходной день. Это значит, что дата закрытия переносится на следующий рабочий день – 21.12.2015 г.

Как влияют на эффективную ставку операции пополнения вклада или частичного снятия.

При пополнении вклада, его основное тело увеличивается, следовательно, клиент получит больше процентов.
Рассмотрим вариант, когда клиент вносит на третий месяц сумму в 20 000 руб.

Месяцы	Кап.сумма, руб	Ставка в месяц	Проценты за месяц, руб
1	100000	0,006	600
2	100600	0,006	603,6
3	121203,6	0,006	727,2216
4	121930,82	0,006	731,5849
5	122662,41	0,006	735,9744
6	123398,38	0,006	740,3903
7	124138,77	0,006	744,8326
8	124883,60	0,006	749,3016
9	125632,91	0,006	753,7974
10	126386,70	0,006	758,3202
11	127145,02	0,006	762,8701
12	127907,89	0,006	767,4474
Итого	8675,341

Итого, общая сумма процентов получится на 1233 руб. больше.

При частичном снятии суммы, итоговая прибыль уменьшится, следовательно, уменьшится и эфф. ставка.

Таким образом, значимое различие между номинальной и эффективной ставкой заметно, если вклад отлежал продолжительный промежуток времени, а капитализация производилась ежемесячно. Клиент сам вправе выбирать, что ему удобнее в той или иной ситуации.

Источник