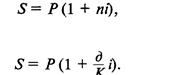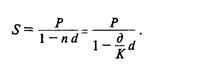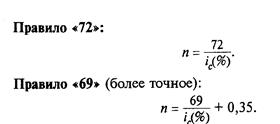Доходность операции при простой ставке ссудного процента
Определение процентной ставки
Уровень процентной ставки является мерой доходности операции, критерием сопоставления альтернатив и выбора наиболее выгодных условий. Из формул
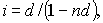
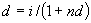
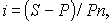
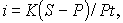
 (3)
(3)
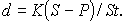
Следует отметить, что срок п, t в этих формулах имеет разный смысл: в (1) и (2) это весь срок операции, а в (3) и (4) — оставшийся срок до погашения.
Определить доходность операции для кредитора, если им предоставлена ссуда в размере 200 тыс. р. на 60 дней и контракт предусматривает сумму погашения долга 210 тыс. р. Доходность выразить в виде простой ставки процентов i и учетной ставки d. Временную базу принять равной К = 360 дней.
По формуле (2.) определим доходность операции в виде простой ставки процентов:
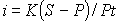
По формуле (4) определим доходность операции в виде простой учетной ставки:
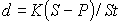
Доходность операции, выраженная в виде простой ставки составляет 30%, а в виде простой учетной ставки – 28,6%.
Источник
Простые ставки ссудных процентов
Простые ставки ссудных (декурсивных) процентов применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет, как правило, срок менее одного года), или когда после каждого интервала начисления кредитору выплачиваются проценты. Естественно, простые ставки ссудных процентов могут применяться и в любых других случаях по договоренности участвующих в операции сторон.
Введем следующие обозначения:
i(%) — простая годовая ставка ссудного процента;
Р — величина первоначальной денежной суммы;
S — наращенная сумма;
п — продолжительность периода начисления в годах;
д — продолжительность периода начисления в днях;
К — продолжительность года в днях. Величина К являетсявременной базой для расчета процентов.
В зависимости от способа определения продолжительности финансовой оперции рассчитывается либо точный, либо обыкновенный (коммерческий) процент.
Простые учетные ставки
При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления (т. е. из наращенной суммы). Эта сумма и считается величиной получаемого кредита (или ссуды). Так как в данном случае проценты начисляются в начале каждого интервала начисления, заемщик, естественно, получает эту сумму за вычетом процентных денег. Такая операция называетсядисконтированием по учетной ставке, а такжекоммерческимилибанковским учетом.
Дисконтом называется доход, полученный по учетной ставке, т. е. разница между размером кредита и непосредственно выдаваемой суммой. Пусть теперь (/(%) — простая годовая учетная ставка;
d — относительная величина учетной ставки;
S — сумма, которая должна быть возвращена;
Р — сумма, получаемая заемщиком.
Тогда, согласно определениям, получаем формулу для определения наращенной суммы:
Пример
Кредит выдается на полгода по простой учетной ставке 40%. Рассчитать сумму, получаемую заемщиком, и величину дисконта, если требуется возвратить 30 000 000 руб.
РешениеПо формуле (2.5) получаем:
Р = 30 000 000 (1 — 0,5 • 0,4) = 24 000 000 руб. Далее:
Д = S — Р = 30 000 000 — 24 000 000 = 6 000 000 руб.
Сложные ставки ссудных процентов
Если после очередного интервала начисления доход (т. е. начисленные за данный интервал проценты) не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулы сложных процентов. Сложные ссудные проценты в настоящее время являются весьма распространенным видом применяемых в различных финансовых операциях процентных ставок.
Основная формула расчета сложного ссудного процента
S=P*(1+i) n
Это основная формула проента применяемая в финансовых расчетах.
Эти правила позволяют определить за какой срок n вложенный капитал увеличится в 2 раза при известной ставке процента i (которая выражается в процентах, а не в долях единицы) Данные правила дают весьма точный результат, отклонения достаточно малы и ими можно пренебречь.
Особые случаи расчета сложного процента
1. Когда в периоде начисления содержится нецелое число интервалов. Например, при ежегодном начислении процента кредит выдается на нецелое число лет
Тогда при расчете по основной формуле мы получим погрешность при возведении в дробную степень.Точный расчет осуществляют по следующей формуле
S=P*(1+i) n a *(1+inb)
Здесь na – целое число интервалов
nb — дробный остаток интервала.
Например, если кредит выдан на 3,5 года при ежегодном начислении процента то na = 3, nb = 0,5
Фактически формула является комбинацией сложного процента (первая скобка) и простого процента (вторая скобка). То есть мы рассчитываем сложный процент за целое число интервалов, а затем рассчитываем простой процент за дробный остаток интервала от всей накопленной суммы
2. Когда процент начисляется несколько раз за временную единицу, в которой выражена ставка процента. Напрмер, дана годовая ставка процента, а процент начисляется раз в полгода, квартал или раз в месяц.
В этом случае формула приобретет следующий вид:
S=P*(1+i/m) n * m
m – количество интервалов начисления в той временной единице, в которой выражена ставка процента
Например, ставка процента годовая. Тогда это количество интервалов начисления в году, то есть сколько раз за год начисляется процент. Если процент начисляется раз в полгода то m=2 (то есть 2 раз за год), если процент начисляется раз в квартал то m=4 (4 раз за год), если процент начисляется раз в месяц то m=12 (12 раз за год) и т.д.
Дата добавления: 2018-03-01 ; просмотров: 1885 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Доходность ссудных и учетных операций с удержанием комиссионных
Ссудные операции. Доходность ссудных операций (без учета комиссионных) измеряется с помощью эквивалентной годовой ставки сложных процентов (см. параграф 3.3). За открытие кредита, учет векселей и другие операции кредитор часто взимает комиссионные, которые заметно повышают доходность операций, так как сумма фактически выданной ссуды сокращается.
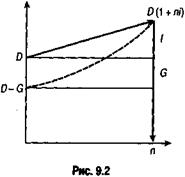
Пусть ссуда в размере D выдана на срок n. При ее выдаче удерживаются комиссионные за операцию (G). Фактически выданная ссуда равна D — G. Пусть для начала сделка предусматривает начисление простых процентов по ставке i. При определении доходности этой операции в виде годовой ставки сложных процентов iЭ исходим из того, что наращение величины D — G по этой ставке должно дать тот же результат, что и наращение D по ставке i. Разумеется, уменьшение фактической суммы кредита связано не только с удержанием комиссионных. Однако для краткости любое удержание денег, сделанное в пользу кредитора, будем называть в этой главе комиссионными.
По определению балансовое уравнение запишем в виде:
Графическое изображение данной сделки (контур) показано на рис. 9.2. Пусть G = D(1 — g), где g — относительная величина комиссионных в сумме кредита, тогда
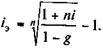
Полученный показатель доходности можно интерпретировать как скорректированную цену кредита.
При расчете iЭ будем полагать, что временная база всегда 365 дней. При начислении процентов на сумму ссуды полагаем, что K = 360 или 365 дней.
Ставка iЭ не фигурирует в условиях операции, она полностью определяется ставкой процентов и относительной величиной комиссионныхпри заданном сроке сделки.
Предположим, что необходимо охарактеризовать доходность в виде ставки простыхпроцентов (iЭП). В этом случае на основе соответствующего балансового уравнения находим
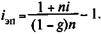
Пример 9.1.При выдаче ссуды на 180 дней под 8% годовых кредитором удержаны комиссионные в размере 0,5% суммы кредита. Какова эффективность ссудной операции в виде годовой ставки сложных процентов? Пусть при начислении процентов K = 365, тогда по формуле (9.2) находим
iЭ = 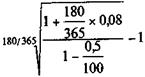
Если ссуда выдается под сложные проценты, то исходное уравнение для определения iЭ имеет вид
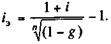
Пример 9.2. В какой мере удержание комиссионных из расчета 1 % суммы кредита увеличивает эффективность ссуды для кредитора при пяти- и десятилетнем сроке?
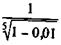
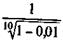
Учетные операции. Если доход извлекается из операции учета по простой учетной ставке, то эффективность сделки без удержания комиссионных определяется по формуле эквивалентной ставки (3.20). При удержании комиссионных и дисконта заемщик получает сумму D — Dd — G. Если дисконт определяется по ставке простых процентов, то эта сумма составит D(1- nd — g). Контур операции показан на рис. 9.3. Балансовое уравнение в данном случае имеет вид
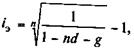
где n — срок, определяемый при учете долгового обязательства.
Для полного показателя доходности в виде iэп находим
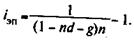
Временная база при расчете iЭ принимается равной 365 дням, в учетной операции — 360 или 365 дням (подробнее см. параграфы 1.3 и 1.6).
Пример 9.3. Вексель учтен по ставке d = 10% за 160 дней до его оплаты. При выполнении операции учета с владельца векселя удержаны комиссионные в размере 0,5%. Доходность операции согласно (9.5) при условии, что временная база учета 360 дней, составит
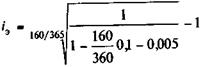
Эффективность без удержания комиссионных — 10,8%.
Во всех рассмотренных случаях искомая ставка iЭ представляет собой частный случай упомянутой выше ПД. Заметим, что влияние комиссионных на iЭ уменьшается по мере увеличения срока сделки.
Удержание комиссионных — не единственная возможность изменения фактической суммы инвестиций по сравнению с номиналом. В практике возможны случаи, когда инвестор несет дополнительные расходы, например приобретая опцион на право купить ценную бумагу. Такие расходы, очевидно, формально можно рассматривать как комиссионные с обратным знаком (-G)и для расчета применять полученные выше формулы (9.2) — (9.6).
Пример 9.4. Всероссийский биржевой банк выпустил в обращение депозитный сертификат (в виде монеты) достоинством 5 тыс. руб. с условиями: продажа по нумизматической стоимости, цена опциона на право покупки 50 руб.; сертификаты принимаются к оплате ВББ по номиналу до 30 декабря 1996 г. и по двойному номиналу через 5 лет, т.е. с 31 декабря 1996 г.
Поставим перед собой задачу определить доходность инвестиций в такой сертификат без учета нумизматической ценности монеты. Инвестор, как было показано, несет дополнительные расходы по приобретению опциона, т.е. G = -50 и, следовательно, g = -50/5000 = -0,01. Учтем также, что в первые пять лет i = 0. Если допустить, что монета будет реализована в качестве платежного средства в ВББ через четыре года после ее выпуска,то получим
iЭ = 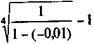
При наступлении права получить двойной номинал имеем 1 + + 5i = 2, отсюда
iЭ = 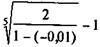
При рассмотрении рисунков 9.2, 9.3 становится очевидным, что контур финансовой операции, основанный на договорной ставке i, может быть дополнен контуром по ставке iЭ. Это позволяет лучше понять сущность ПД, по крайней мере в рамках рассмотренных простых сделок. Кроме того, становится очевидным вклад комиссионных в общий доходпо сделке.
Источник
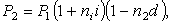
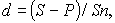 (3)
(3)