Доходность операции для кредитора по простой учетной ставке

Доходность операций

Определение доходности операции по простой процентной ставке наращения при временной базе. Расчет суммы возврата при предоставлении ссуды на условиях ежеквартального начисления процентов по смешанной схеме. Вычисление эффективной процентной ставки.

Рубрика	Финансы, деньги и налоги
Вид	задача
Язык	русский
Дата добавления	02.11.2013
Размер файла	33,4 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

1. Банк учитывает вексель за 210 дней до срока по простой учетной ставке 12%, используя временную базу в 365 дней. Определить доходность такой операции по простой процентной ставке наращения при временной базе, равной 360.

ссуда процентный ставка начисление

S = P * (1 — t/k * d), отсюда:

P/S = 1 — 210/365 *0,12 = 0,93

d = (1 — 0,93) / (210/360) = 0,120 (12 %)

2. Банк предоставил ссуду в размере 10 тыс. руб. на 37 месяцев под 11% годовых на условиях ежеквартального начисления процентов по смешанной схеме. Какую сумму предстоит вернуть банку по истечении срока?

r = 0,12 (количество кварталов в 37 месяцах)

3. Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов (ежегодно, ежемесячно, ежедневно) и номинальной ставке сложных процентов равной 10%. Количество дней в году принять равным 365.

m = 1; 12; 365 дней

4. Срок оплаты векселя составляет 3 месяца по сложной учетной ставке 27%. Оценить доходность операции по эквивалентным номинальной ставке дисконтирования и силе роста, если номинальная ставка начисляется раз в полгода.

Размещено на Allbest.ru

Подобные документы

Определение вексельной суммы, процентной ставки, эквивалентной банковской учетной ставке. Расчет реальной годовой доходности по облигациям при заданных номинальной процентной ставке и уровне инфляции. Ожидаемая реальная доходность держателя векселя.

контрольная работа [26,4 K], добавлен 21.12.2012

Методика определения суммы платежа с применением ставки сложных процентов. Расчет доходности операции для кредитора в виде простой, сложной процентной и учетной ставки. Вычисление предпочтительного варианта вложения денег при заданных процентных ставках.

контрольная работа [38,1 K], добавлен 26.03.2013

Определение суммы процента за кредит при германской и английской практике. Начисление процентов за кредит, погашенный единовременным платежом. Расчет ставки процентов по кредиту с учетом инфляции. Доходность вкладов по годовой ставке сложных процентов.

задача [19,5 K], добавлен 14.11.2009

Вычисление эффективной ставки процента. Определение цены кредита в виде простой годовой учетной ставки и годовой ставки простых процентов, множителя наращения за весь срок договора, процента и суммы накопленного долга, доходности операции для кредита.

контрольная работа [27,6 K], добавлен 21.12.2013

Методика финансовых вычислений в схеме простых процентов с учетом инфляции. Сущность инфляционного обесценения денег. Применение модели американского экономиста И. Фишера. Определение простой процентной ставки при выдаче кредита и наращенной суммы долга.

курсовая работа [489,9 K], добавлен 21.05.2014

Источник

Расчет простых и сложных процентов, процентной ставки банка

Особенности определения суммы, причитающейся в качестве процентов по кредиту, суммы, причитающейся к возврату. Определение процентной ставки банка. Расчет множителя наращения процентов по капиталу за срок договора. Доходность операции для кредитора.

Рубрика	Банковское, биржевое дело и страхование
Вид	контрольная работа
Язык	русский
Дата добавления	19.02.2012

Определить сумму, причитающуюся в качестве процентов по кредиту и сумму, причитающуюся к возврату, если сумма кредита составляет 50000 ден. ед., срок 3 месяца при ставке простых процентов равной 15%, построить график зависимости S(t) суммы долга по простым процентам по времени.

При начислении простых процентов по ставке i за базу берётся первоначальная сумма долга. Наращённая сумма S растёт линейно во времени.

Наращённую сумму можно представить в виде двух слагаемых: первоначальной суммы Р и суммыпроцентов I:

I = 50000 * 3/12*0,15=1875 ден. ед.

S= 50000+1875=51875 ден.ед.

Рис.1. График зависимости S(t) по времени.

В банк положено 50000 руб., а через 1,5 года на счете было 110000 руб. Определите ставку процентов банка, проценты простые точные.

Ставка процента банка составила 80% годовых.

В договоре, рассчитанном на год, принята ставка простых процентов на первый квартал в размере 3% годовых, а на каждый последующий на 0,9 больше, чем в предыдущем. Определить множитель наращения за весь срок договора

Процентные ставки не остаются неизменными во времени, поэтомув кредитных соглашениях предусматриваются дискретно изменяющиеся во времени процентные ставки. В этом случае формула расчёта наращенной суммы принимает следующий вид:

где P — первоначальная сумма; i — ставка простых процентов в периоде с номером t = m ,1;

n — продолжительность t периода начисления по ставке it.

За весь период договора ставка простых процентов составит 1,0435.

Определить доходность операции для кредитора, если им предоставлена ссуда в размере 300000 руб. на 90 дней и договор предусматривает сумму погашения долга 360000 руб. Доходность выразить в виде простой ставки I и ставке d. Временную базу принять равной К=365 дней.

Доходность операции на основе простой ставки называется число, определяемой по формуле:

Доходность операции для кредитора составила 81%.

Определим простую учетную ставку:

Простая учетная ставка составляет 45,22 %.

В договоре зафиксирована переменная ставка сложных процентов, определяемая как 15%годовых, плюс маржа 3% в первый год, 5% — во второй, 6% в третий год. Определить величину множителя наращения

Величина множителя за первый год

Величина множителя за второй год

Величина множителя за третий год

В результате расчета установили, что величина множителя наращения за три года составила 2,0193.

Определить какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку 15% годовых.

Где m- число интервалов начисления процентов = 4.

ЕРR- эффективная годовая ставка=15%

Номинальная ставка при ежеквартальном начислении равна 14,2% годовых.

Рассчитать эквивалентную силу роста при годовой ставке 25%.

Эквивалентная сила роста рассчитывается по формуле:

Эквивалентная сила роста составляет 20% годовых.

На депозит со ставкой 11% годовых помещены денежные средства сроком на 1 год. Инфляция составляет 8% в год. Найти реальную ставку для случая простых и сложных процентов.

Годовая процентная ставка простых процентов, учитывающая инфляцию

Годовая процентная ставка простых процентов, учитывающая инфляцию

Список использованной литературы

процент кредит банк

1. Самаков К.Л. Финансовая математика: сборник задач с решениями: Учебное пособие:- М.: Альфа-М; ИНФРА-М, 2009.

2. Е.М. Четыркин. Финансовая математика: Учебник.-М.: «ДелоЛТД», 2002

3. Финансовая математика: учебное пособие/ Е.В. Ширшов, Н.И. Петрик, А.Г. Тутыгин, Т.В. Меньшикова.-5-е изд., перераб. ми доп. — М.: КНОРУС, 2010

Подобные документы

Особенности расчета процентной ставки при сложном и простом проценте. Сроки выплаты кредита, взятого под простую ставку. Определение величины взноса при начислении процентов ежеквартально по ставке сложных процентов годовых для накопления заданной суммы.

контрольная работа [23,8 K], добавлен 29.10.2012

Срок удвоения капитала при начислении сложных процентов раз в год по процентной ставке. Схема начисления сложных процентов, сравнение эффективной и номинальной ставок. Определение ставки по кредиту с целью получения дохода с учетом темпа инфляции.

курсовая работа [465,6 K], добавлен 26.09.2011

Формула для определения простой ставки процентов по кредиту, компенсирующей ожидаемую инфляцию. Расчет ставки, которую использовал банк при учете векселя. Задача на определение суммы, которую получит владелец депозита, по окончанию срока договора.

контрольная работа [22,4 K], добавлен 19.04.2011

Определение накопленной суммы денег и величины процентных денег по вкладам при английской, французской и германской практиках. Расчет ставки процентов по кредиту с учетом инфляции, погашенной суммы и суммы начисленных процентов. Расчет величины ренты.

контрольная работа [27,9 K], добавлен 05.12.2011

Определение уровня процентной ставки при осуществлении финансовых операций, размера долга для различных вариантов начисления процентов по кредитам. Расчет суммы, полученной владельцем векселя и величины дисконта, эквивалентной годовой учетной ставки.

контрольная работа [24,8 K], добавлен 15.10.2010

Условия открытия депозитного вклада. Определение будущей суммы денег, которую получит клиент банка по окончании срока договора вклада. Определение погашаемой суммы и суммы процентов за кредит по простой ставке процентов 12 и 15 процентов годовых.

контрольная работа [10,8 K], добавлен 25.02.2014

Порядок досрочного востребования суммы вклада. Вклад интересных процентов «Абсолютный лидер тест-драйв». Определение процентной ставки при заключении договора. Порядок начисления и уплаты процентов. Условия пролонгации или досрочного расторжения.

контрольная работа [19,9 K], добавлен 12.10.2014

Определение средневзвешенной ставки процентов по выданным кредитам. Вычисление доходности по кредиту. Анализ структуры активов по степени ликвидности и риска. Расчет чистой процентной маржи и дисбаланса средневзвешенных сроков погашения задолженности.

лабораторная работа [48,3 K], добавлен 13.09.2012

Определение процентов, при которой первоначальный капитал достигнет через 180 дней заданной суммы. Вычисление размеров долга для вариантов начисления процентов. Расчет суммы на счете клиента к концу срока вклада. Определение дисконтированной величины.

контрольная работа [35,9 K], добавлен 15.11.2010

Финансирование оборотного капитала предприятия. Определение суммы погашения кредита и суммы начисленных процентов. Начисление сложных процентов. Расчёт суммы выплат по депозиту и дохода по облигации. Коммерческий вексель с дисконтированной ставкой дохода.

контрольная работа [27,5 K], добавлен 13.01.2014

Источник

Доходность ссудных и учетных операций с удержанием комиссионных

Ссудные операции. Доходность ссудных операций (без учета комиссионных) измеряется с помощью эквивалентной годовой ставки сложных процентов (см. параграф 3.3). За открытие кредита, учет векселей и другие операции кредитор часто взимает комиссионные, которые заметно повышают доходность операций, так как сумма фактически выданной ссуды сокращается.

Пусть ссуда в размере D выдана на срок n. При ее выдаче удерживаются комиссионные за операцию (G). Фактически выданная ссуда равна D — G. Пусть для начала сделка предусматривает начисление простых процентов по ставке i. При определении доходности этой операции в виде годовой ставки сложных процентов i_Э исходим из того, что наращение величины D — G по этой ставке должно дать тот же результат, что и наращение D по ставке i. Разумеется, уменьшение фактической суммы кредита связано не только с удержанием комиссионных. Однако для краткости любое удержание денег, сделанное в пользу кредитора, будем называть в этой главе комиссионными.

По определению балансовое уравнение запишем в виде:

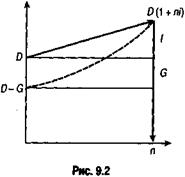
Графическое изображение данной сделки (контур) показано на рис. 9.2. Пусть G = D(1 — g), где g — относительная величина комиссионных в сумме кредита, тогда

(9.2)

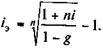
Полученный показатель доходности можно интерпретировать как скорректированную цену кредита.

При расчете i_Э будем полагать, что временная база всегда 365 дней. При начислении процентов на сумму ссуды полагаем, что K = 360 или 365 дней.

Ставка i_Э не фигурирует в условиях операции, она полностью определяется ставкой процентов и относительной величиной комиссионныхпри заданном сроке сделки.

Предположим, что необходимо охарактеризовать доходность в виде ставки простыхпроцентов (i_ЭП). В этом случае на основе соответствующего балансового уравнения находим

(9.3)

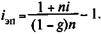
Пример 9.1.При выдаче ссуды на 180 дней под 8% годовых кредитором удержаны комиссионные в размере 0,5% суммы кредита. Какова эффективность ссудной операции в виде годовой ставки сложных процентов? Пусть при начислении процентов K = 365, тогда по формуле (9.2) находим

i_Э = 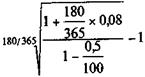= 0,0927, или 9,27%

Если ссуда выдается под сложные проценты, то исходное уравнение для определения i_Э имеет вид

(9.4)

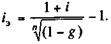
Пример 9.2. В какой мере удержание комиссионных из расчета 1 % суммы кредита увеличивает эффективность ссуды для кредитора при пяти- и десятилетнем сроке?

= 1,002, т.е. на 0,2%;

= 1,001, или 0,1%

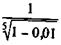
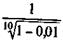
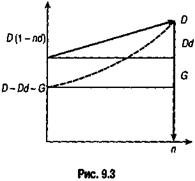
Учетные операции. Если доход извлекается из операции учета по простой учетной ставке, то эффективность сделки без удержания комиссионных определяется по формуле эквивалентной ставки (3.20). При удержании комиссионных и дисконта заемщик получает сумму D — Dd — G. Если дисконт определяется по ставке простых процентов, то эта сумма составит D(1- nd — g). Контур операции показан на рис. 9.3. Балансовое уравнение в данном случае имеет вид

(9.5)

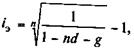
где n — срок, определяемый при учете долгового обязательства.

Для полного показателя доходности в виде i_эп находим

(9.6)

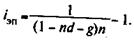
Временная база при расчете i_Э принимается равной 365 дням, в учетной операции — 360 или 365 дням (подробнее см. параграфы 1.3 и 1.6).

Пример 9.3. Вексель учтен по ставке d = 10% за 160 дней до его оплаты. При выполнении операции учета с владельца векселя удержаны комиссионные в размере 0,5%. Доходность операции согласно (9.5) при условии, что временная база учета 360 дней, составит

= 0,123, т. е. 12,3%.

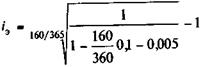
Эффективность без удержания комиссионных — 10,8%.

Во всех рассмотренных случаях искомая ставка i_Э представляет собой частный случай упомянутой выше ПД. Заметим, что влияние комиссионных на i_Э уменьшается по мере увеличения срока сделки.

Удержание комиссионных — не единственная возможность изменения фактической суммы инвестиций по сравнению с номиналом. В практике возможны случаи, когда инвестор несет дополнительные расходы, например приобретая опцион на право купить ценную бумагу. Такие расходы, очевидно, формально можно рассматривать как комиссионные с обратным знаком (-G)и для расчета применять полученные выше формулы (9.2) — (9.6).

Пример 9.4. Всероссийский биржевой банк выпустил в обращение депозитный сертификат (в виде монеты) достоинством 5 тыс. руб. с условиями: продажа по нумизматической стоимости, цена опциона на право покупки 50 руб.; сертификаты принимаются к оплате ВББ по номиналу до 30 декабря 1996 г. и по двойному номиналу через 5 лет, т.е. с 31 декабря 1996 г.

Поставим перед собой задачу определить доходность инвестиций в такой сертификат без учета нумизматической ценности монеты. Инвестор, как было показано, несет дополнительные расходы по приобретению опциона, т.е. G = -50 и, следовательно, g = -50/5000 = -0,01. Учтем также, что в первые пять лет i = 0. Если допустить, что монета будет реализована в качестве платежного средства в ВББ через четыре года после ее выпуска,то получим

i_Э = 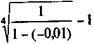= -0,002, т.е. — 0,2%.

При наступлении права получить двойной номинал имеем 1 + + 5i = 2, отсюда

i_Э = 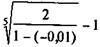= 0,1464, т. е. 14,64%.

При рассмотрении рисунков 9.2, 9.3 становится очевидным, что контур финансовой операции, основанный на договорной ставке i, может быть дополнен контуром по ставке i_Э. Это позволяет лучше понять сущность ПД, по крайней мере в рамках рассмотренных простых сделок. Кроме того, становится очевидным вклад комиссионных в общий доходпо сделке.

Источник