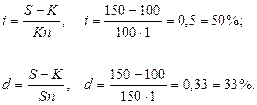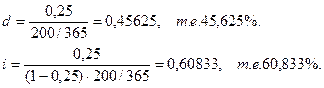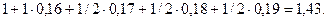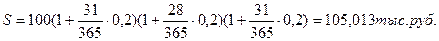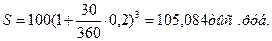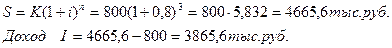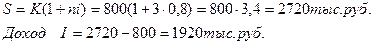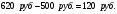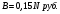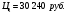Формулы доходности финансовых операций



Если в формулах наращения по процентной и учетной ставке принять срок n = 1 году, то получим, что
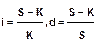
Если n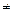
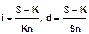
Эти формулы принято называть формулами доходности или эффективности по простой ставке процентов и учетной ставке соответственно.
Предприятие получило кредит на 1 год в размере 100 млн. с условием возврата 150 млн.
Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок.
К = 100 млн., S = 150 млн., n = 1 год. I = ?, d = ?
Решение:
Дисконтная ставка всегда меньше процентной, ибо она учитывает время более жестко.
Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли (или процента) от суммы погасительного платежа. Таким образом, уровень процентной ставки задается в неявном виде. Выведем формулы, с помощью которых можно вычислить значения этих ставок.
Пусть S- размер погасительного платежа (сумма ссуды к концу срока),
dn – доля этого платежа, определяющая величину дисконта за весь срок ссуды.
К = S(1 – dn) – реально выдаваемая ссуда в момент заключения договора.
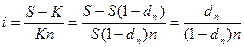 |
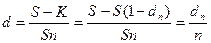 |
Задача 7.
Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней.
Простые переменные ставки
В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.
Если i1, i2,… ik – последовательные во времени простые ставки,
а n1, n2,… nk – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:
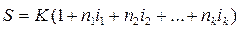 |
Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.
Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года.
Множитель наращения =
Иначе, за 2,5 года начальный капитал увеличился в 1,43 раза.
Реинвестирование
В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!)
В этом случае наращенная сумма для всего срока составит:
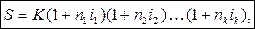
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:
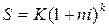
Задача 9.
Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам.
По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам.
По точным процентам:
(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!)
По банковским процентам при условии, что в каждом месяце по 30 дней:
Модуль 2. Сложные проценты
Наращение по сложным процентам
В среднесрочных и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты.
Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов.
Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид

(1) 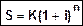
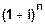
Задача 1.
Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.
2. Простые проценты:
За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам.
Задача 2.
Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.
Источник
Задачи к зачёту / РЦБ- ДОХОД И ДОХОДНОСТЬ
ДОХОД И ДОХОДНОСТЬ
Курс пакета акций из 800 штук вырос за год на 60% и составил 22 000 руб., дивиденд выплачивается раз в полугодие в размере 6 руб. на акцию. Определить полную доходность пакета акций за год.
Доход по дивидендам за год =
Начальная стоимость пакета акций = 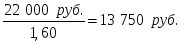
Полная доходность пакета акций

Депозитный сертификат был куплен за 20 000 руб. за восемь месяцев до его погашения и продан за 22 000 руб. за пять месяцев до погашения. Определите доходность этой операции в процентах годовых.
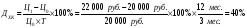
Дилер владел финансовым инструментом 18 дней и получил в этот период купонный доход 1 200 руб., рыночная цена финансового инструмента в течение периода оставалась неизменной – 14 000 руб. Определите доходность этой операции в процентах годовых.
Доходность в процентах годовых:

Курс облигации вырос за год на 20% и составил 8 000 руб., процент выплачивается раз в полугодие в размере 600 руб. Определить полную доходность облигации за год.
Начальный курс облигации = 
Процентный доход по облигации за год 
Полная доходность облигации за год:

Определите совокупный доход по акции, если известно, что акция приобретена по номинальной стоимости 500 руб. при ставке дивиденда 15% годовых. Рыночная цена акции через год после выпуска составила 620 рублей.
Совокупный доход = доход от изменения стоимости акции + дивидендный доход.
Капитализированный доход =
Дивидендный доход = 
Совокупный доход =
Какова будет доходность операции в процентах годовых, если инвестор купил по номиналу, а через два месяца продал на 15% дороже пакет облигаций с купоном 12% годовых с ежемесячной выплатой процентов по купону?
Пусть N – номинал облигации. Тогда:
Купонные платежи за период в 2 месяца = 2% от N= 0,02N
Цена продажи пакета облигаций = 1,15 N
Доходность операции в процентах за период = ((0,15N + 0,02N)/ N ) х 100% = 17%
Доходность в % годовых = (17/2) х 12 = 102%
Привилегированная акция с дивидендом 15% приобретена по цене, равной 2,75 номинальной стоимости, и продана через год за 21 000 руб., обеспечив полную доходность в 70%. Определите, за какую цену была приобретена акция.
Обозначим за N номинал акции. Тогда:
цена покупки акции 
выплата дивидендов по акции
Используя формулу доходности акции, 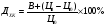
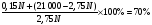
Цена покупки
Определите доходность акции в процентах, если известно, что акция приобретена по номинальной стоимости 500 руб. при ставке дивиденда 15,25% годовых. Рыночная цена акции через восемь месяцев после выпуска составила 620 рублей.
Выплата дивидендов за 8 месяцев 
Доходность 
Акция, номиналом 24 000 руб. со ставкой годового дивиденда 14% приобретена по номиналу и продана через год, обеспечив её владельцу 0,4 руб. дохода с каждого инвестируемого рубля.
Определить цену акции при продаже.
Выплата дивидендов 
За 
Используя формулу доходности акции, 


Какова будет доходность операции в процентах годовых, если инвестор купил по номиналу, а через четыре месяца продал на 18% дороже пакет акций с дивидендом 12% годовых с ежемесячной выплатой процентов?
Обозначим за N номинал акции.
Выплата дивидендов за период владения акцией 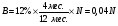
Цена продажи пакета акций 
Доходность операции в процентах годовых

Облигация номиналом 100 руб. с купонной ставкой 10% годовых и периодом обращения – 1 год имеет рыночную цену, равную 75.0. Рассчитать текущую рыночную доходность и доходность к погашению.
Текущая рыночная доходность 


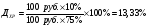
Доходность к погашению 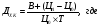



Рассчитать накопленный купонный доход по облигации с купонной ставкой 10% годовых, если с даты купонной выплаты прошло 3 месяца.
Решение: Накопленный купонный доход
Источник