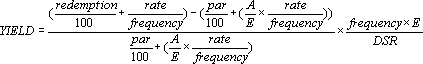Доходность облигации формула эксель

Excel для финансиста

Поиск на сайте

Расчёт эффективной доходности облигации к погашению

Эффективная доходность облигации отличается от простой тем, что в расчёт доходности включен доход от возможного реинвестирования купонного дохода в эту же ценную бумагу. Естественно, эффективная доходность больше простой.

Расчёт эффективной доходности существенно сложнее расчёта простой доходности. В Excel есть два инструмента, немного отличающиеся результативностью.

Самый простой инструмент — функция ДОХОД, у неё 7 аргументов:

• дата покупки облигации;
• дата погашения;
• процентная ставка купонных выплат в %;
• текущая цена покупки («грязная» цена), приведённая к 100% от номинала (если облигация сейчас стоит 1078 руб. с учётом НКД, делим на 10, чтобы получилось 107,8);
• цена погашения (обычно равна номиналу, если нет амортизации или оферты с особыми условиями);
• базис — способ вычисления дня. В формуле использован фактический базис (один день равен календарному), подробнее о вариантах базиса смотрите в справке Excel.

Скачайте файл с примером: doh_obl_eff. В ячейке С24 рассчитана доходность облигации ОФЗ-26218-ПД при покупке на дату 25.05.2018. Формула имеет вид: «=ДОХОД(СЕГОДНЯ();C6;C9;C15/10;100;2;1)»:

(Исходные данные для расчёта можно взять на специализированных сайтах типа rusbonds.ru, cbonds.info, bonds.finam.ru и многих других).

Как видим, эффективная доходность выше простой, как и ожидалось.

Рассмотрим теперь более универсальный метод расчёта. Ограничение функции ДОХОД в том, что она работает для случаев периодических выплат купонов (2,4,6 в год), причём по фиксированной ставке, и не может быть прямо использована в случаях частичной амортизации облигации. В более сложных случаях лучше использовать функцию ЧИСТВНДОХ, которая рассчитывает эффективную доходность на основе финансовых потоков.

В файле примера справа создана таблица финансовых потоков. Первая строчка в ней — операция покупки облигации по «грязной» цене, сумма обязательно должна быть отрицательным значением. Далее перечислены операции по выплате купонов, данные также скопированы с сайта rusbonds, за исключением уже выплаченных купонов. Если по облигации предусмотрена амортизация (частичное погашение номинала), то эти операции также нужно будет отразить в таблице. Самая последняя операция — погашение облигации. Ещё ниже рассчитана прибыль как сумма всех финансовых потоков (платежей и поступлений).

В ячейке G37 рассчитана эффективная доходность облигации к погашению с помощью функции ЧИСТВНДОХ. Как видим, формула имеет очень простой вид: «=ЧИСТВНДОХ(G4:G34;F4:F34;8%)» В ней три аргумента: диапазон дат операций, суммы операций и третий необязательный аргумент — ориентировочное значение ответа, для облегчения работы алгоритма Excel.

расчет эффективной доходности облигации двумя методами

Скачать пример расчёта эффективной доходности облигации ОФЗ: doh_obl_eff

Отметим, что для малого горизонта инвестирования (до 3 лет) рассчитывать эффективную доходность облигации — не очень информативное занятие, так как реинвестировать купонный доход в эту же ценную бумагу вряд ли получится. Зачастую нагляднее рассчитывать простую эффективность облигации. Пример расчёта простой эффективность облигации ОФЗ в Excel был рассмотрен нами ранее. Смотрите статью: Расчет простой доходности облигации к погашению

Источник

Функция ДОХОД

В этой статье описаны синтаксис формулы и использование функции ДОХОД в Microsoft Excel.

Описание

Возвращает доходность ценных бумаг, по которым производятся периодические выплаты процентов. Функция ДОХОД используется для вычисления доходности облигаций.

Синтаксис

ДОХОД(дата_согл; дата_вступл_в_силу; ставка; цена; погашение, частота; [базис])

Важно: Даты должны быть введены с использованием функции ДАТА или как результат вычисления других формул и функций. Например, для указания даты 23 мая 2008 г. воспользуйтесь выражением ДАТА(2008,5,23). Если ввести даты как текст, это может привести к возникновению проблем.

Аргументы функции ДОХОД описаны ниже.

Дата_согл — обязательный аргумент. Дата расчета за ценные бумаги (дата продажи ценных бумаг покупателю, более поздняя, чем дата выпуска).

Дата_вступл_в_силу — обязательный аргумент. Срок погашения ценных бумаг. Эта дата определяет момент, когда истекает срок действия ценных бумаг.

Ставка — обязательный аргумент. Годовая процентная ставка для купонов по ценным бумагам.

Цена — обязательный аргумент. Цена ценных бумаг на 100 рублей номинальной стоимости.

Погашение — обязательный аргумент. Выкупная стоимость ценных бумаг на 100 рублей номинальной стоимости.

Частота — обязательный аргумент. Количество выплат по купонам за год. Для ежегодных выплат частота равна 1, для полугодовых — 2, для ежеквартальных — 4.

Базис — необязательный аргумент. Используемый способ вычисления дня.

Способ вычисления дня

Американский (NASD) 30/360

Замечания

В приложении Microsoft Excel даты хранятся в виде последовательных чисел, что позволяет использовать их в вычислениях. По умолчанию дате 1 января 1900 года соответствует номер 1, а 1 января 2008 года — 39448, так как интервал между этими датами составляет 39 448 дней.

Дата соглашения является датой продажи покупателю купона, например облигации. Срок платежа представляет собой дату истечения срока действия купона. Предположим, например, что облигация со сроком действия 30 лет выпущена 1 января 2008 г. и приобретена покупателем через шесть месяцев после выпуска. Датой выпуска будет 1 января 2008 г., датой расчета — 1 июля 2008 г., а срок погашения такой облигации наступит 1 января 2038 г., то есть через 30 лет после даты выпуска.

Значения аргументов «дата_согл», «дата_вступл_в_силу», «частота» и «базис» усекаются до целых.

Если «дата расчета» или «дата погашения» не является допустимой датой, возвращается #VALUE! значение ошибки #ЗНАЧ!.

Если ставка 4, возвращается #NUM! значение ошибки #ЗНАЧ!.

Если «≥» является сроком погашения, то доход возвращает #NUM! значение ошибки #ЗНАЧ!.

Если только один или менее периодов купона укладываются до даты погашения, функция ДОХОД вычисляется следующим образом:

A = количество дней от начала периода купона до даты расчета (накопленные дни).

DSR = количество дней от даты расчета до даты погашения.

E = количество дней в периоде купона.

Если до погашения укладывается более одного периода купона, функция ДОХОД вычисляется итеративным методом (не более 100 итераций). Используется метод Ньютона на основе формулы для функции ЦЕНА. Доходность меняется до тех пор, пока вычисляемая цена для данной доходности не станет близкой к значению аргумента «цена».

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Источник

Как рассчитать доход по облигациям, используя функции Excel

Excel предлагает ряд функций, используемых для вычисления различных финансовых показателей облигаций. Облигацией называется финансовый инструмент, в котором покупатель выступает в роли заимодателя, а учреждение или государство, выпустившее облигации, — в роли заемщика. Однако многие функции, связанные с облигациями, выходят за рамки материала настоящей книги. В этой статье представлены примеры некоторых наиболее распространенных функций.

Некоторые свойства облигаций являются также и аргументами функций, связанных с облигациями.

• Расчетный день. Дата, в которую долговые обязательства переходят к покупателю.
• Срок погашения. Дата, в которую заем (представленный облигацией) возвращается покупателю.
• Ставка (также называемая купоном). Процентная ставка, которую выпустивший облигацию выплачивает покупателю.
• Доходность. Норма прибыли, получаемая покупателем. Включает в себя выплаты по процентам и дисконт.
• Погашение. Выкупная стоимость ценных бумаг за 100 долларов номинальной стоимости.
• Частота. Количество выплат дивидендов за год.

Оценка облигаций

Предприятия, выпускающие ценные бумаги, устанавливают перечисленные выше показатели, основываясь на текущей рыночной конъюнктуре. Когда конъюнктура меняется, стоимость облигаций тоже изменяется.

Для примера предположим, что некоторая компания выпустила облигации с номинальной стоимостью 100 долларов, сроком погашения 10 лет и 6%-ной ставкой, выплачиваемой дважды в год.

• Если процентная ставка по кредитам растет, ставка в 6% становится не такой уж и привлекательной. Покупатели уже не захотят платить 100 долларов за облигацию — они будут их покупать за меньшую сумму.
• Если процентная ставка по кредитам падает, ставка в 6% становится привлекательной. В данном случае покупатели готовы платить больше номинальной стоимости.

Функция ЦЕНА вычисляет сумму, которую покупатели потенциально готовы заплатить за облигацию в ожидании определенного дохода. Синтаксис этой функции таков: ЦЕНА(расчетный_день;срок_погашения;ставка;доходность;погашение;частота;базис ). Учитывая приведенные выше факты, инвестор, желающий получить 7,5% годовых, должен использовать следующую формулу для вычисления приемлемой цены облигации, срок погашения которой наступает через 8 лет: =ЦЕНА(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;,075;100;2) .

Результатом этой формулы будет 91,10 долларов — именно такую сумму стоит заплатить за облигацию номиналом в 100 долларов с шестью процентами годовых, чтобы прибыльность составила 7,5%. Каждый год инвестор будет получать 6%*100 долларов, плюс при погашении облигации он получит дополнительную прибыль в 8,90 долларов. Эти два компонента — проценты и дисконт — формируют доходность облигаций. Фактическая дата выпуска облигации может отличаться от даты ее покупки инвестором. Облигации выпускают многие организации, так производитель кондиционеров кватро клима имеет достаточно высокую ликвидность своих ценных бумаг, которая основывается на качестве продукции.

В рассмотренном примере облигации были выпущены за два года до их покупки, следовательно, инвестор будет получать за них проценты только в течение 8 лет. Если же процентная ставка упала с момента выпуска и инвестору достаточно 5,2%, формула слегка изменится: =ЦЕНА(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;,052;100;2) . При этих обстоятельствах инвестор может заплатить за стодолларовую облигацию 105,18 долларов. На рис. 11.17 эти вычисления показаны на рабочем листе.

Вычисление доходности

В предыдущем примере инвестор знал необходимую ему доходность и вычислял такую цену облигации, чтобы получить ее. Если же, наоборот, он знает цену облигации, то функция ДОХОД поможет вычислить прибыльность инвестиций. Синтаксис этой функции следующий: ДОХОД (расчетный_день;срок_погашения;ставка;цена_покупки;номинал;частота;базис) .

Рис. 1. Использование функции ЦЕНА

Инвестор все еще заинтересован в покупке десятилетней облигации с 6 процентами, выплачиваемыми дважды в год, однако на этот раз он хочет заплатить всего 93,95 долларов за стодолларовую облигацию. Следующая формула вычисляет процентную ставку за восемь лет, оставшихся до даты погашения: =ДОХОД(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;93,95;100;2 ). Если инвестор заплатит за облигацию 93,95 долларов, то получит от своих инвестиций 7%. Если бы он заплатил за облигацию больше ста долларов, то получил бы от инвестиций меньше 6% (рис. 2).

Рис. 2. Когда цена выше номинальной стоимости облигации, прибыльность ниже купона

Источник

Excel для финансиста

Поиск на сайте

Расчет простой доходности облигации к погашению

Простая доходность облигации — это доходность, рассчитанная в %годовых и зависящая от суммы купонного дохода по облигации и разницы в стоимости самой облигации в моменты покупки и продажи. От эффективной доходности отличается тем, что в расчёт не принимается возможность реинвестирования полученного купонного дохода в данную облигацию.

Считаю, что простую доходность облигации уместно использовать, если выбранный срок инвестирования в облигацию невысок (например, до 2 лет) и сумма инвестирования невелика. В таком случае полученного купонного дохода просто не хватит для реинвестирования, и эффективную доходность считать нет смысла.

В данном примере разберём расчёт простой доходности облигации к погашению на примере одной из популярных государственных облигаций (ОФЗ) ОФЗ-26218-ПД. Расчёт других облигаций (муниципальных и корпоративных) ничем принципиально не отличается от расчёта доходности ОФЗ.

Пример представлен для случая покупки ОФЗ через брокерскую контору, принцип расчёта доходности так называемых «народных ОФЗ«, приобретаемых через банки, немного другой (есть дополнительные комиссии и условия досрочного возврата) и будет рассмотрен отдельно.

Для расчёта необходимо знать следующие данные:

• номинал облигации (с учётом прошедшей амортизации),
• дату погашения облигации (в этом простом примере не будем рассматривать доходность к оферте),
• ставка купонов (в % годовых),
• сколько купонов в год выплачивается (при равномерной выплате),
• дату последнего выплаченного купона,
• текущая рыночная цена (в % от номинала).

Всю эту информацию можно найти на специализированных сайтах типа rusbonds.ru, cbonds.info, bonds.finam.ru и многих других.

Итак, расчёт простой доходности облигации к погашению ОФЗ-26218-ПД. Это облигация подходит для простого расчёта, так как есть постоянная доходность (размер купона не меняется) и нет амортизации (то есть номинал неизменен). Для случаев амортизируемых облигаций и переменных купонов лучше использовать другие способы, которые рассмотрим отдельно.

В первых строках размещена общая информация об облигации. В ячейке С7 рассчитывается срок до погашения простой формулой «=C6-СЕГОДНЯ()«.

Обратите внимание, что пример сохранён 25.05.2017, в другой день все расчёты будут иными.

В строке 11 рассчитывается число купонов для погашения формулой «=ОКРУГЛВНИЗ(C7/365;0)*C10+1«: вычисляем количество полных лет до погашения, умножаем на количество купонов в год и добавляем 1 (так как последний купон выплачивается в момент погашения).

В строке 13 рассчитывается накопленный купонный доход (НКД) формулой «=(СЕГОДНЯ()-C12)/365*C9*C5«: он зависит от текущей даты, даты последней выплаты купона, купонной доходности и номинала.

С помощью рассчитанного НКД и цены, по которой облигация торгуется на рынке («чистой цены»), рассчитывается так называемая «грязная цена» — стоимость, которую необходимо заплатить за покупку облигации (без учёта брокерских комиссий). Это сумма инвестиций.

В строках 17-20 рассчитывается доход от инвестирования в облигацию ОФЗ, равный доходу от погашения облигации плюс купонный доход за всё время инвестирования.

В строке 22 рассчитана прибыль, равная разности дохода и сумме инвестиций. В строке 23 — она же в процентном виде. Видим, что за время инвестирования сумма инвестиций более чем удвоилась, но срок очень долгий (14 лет) и простая доходность к погашению составила всего лишь 7,35%.

Эту таблицу можно использовать для расчёта простой доходности к погашению любых облигаций, которые имеют фиксированный купон и не предусматривают амортизацию номинала. Для более сложных случаев стоит составить таблицу платежей и поступлений (финансовых потоков) и использовать функцию Excel ЧИСТВНДОХ, как это сделано в следующем примере расчёта эффективной доходности облигации ОФЗ, смотрите соответствующую статью Расчёт эффективной доходности облигации к погашению.

Скачать пример расчёта простой доходности облигации ОФЗ к погашению : doh_obl_prost

Источник