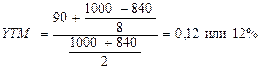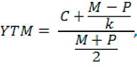Доходность облигации без права досрочного погашения

Финансовый менеджмент: Учебник

Глава 5. Финансовые решения в отношении активов хозяйствующего субъекта

5.2. Финансовые активы; оценка и управление

5.2.7. Доходность облигации без права досрочного погашения

Мы рассмотрели способы оценки стоимости финансовых активов. Другими важными критериями принятия решения о целесообразности покупки или продажи активов, являются показатели доходности.

Доходность входит в число показателей эффективности и используется применительно к финансовым активам и капиталу. Это относительный показатель, рассчитываемый соотнесением дохода (D), генерируемого данным финансовым активом, и величины инвестиции (IC) в этот актив, т.е. в наиболее общем виде он может быть представлен следующим образом:

В зависимости от вида финансового актива в качестве дохода D чаще всего выступают дивиденд, процент, прирост капитализированной стоимости.

Таким образом, существуют различные варианты расчета доходности. Этот показатель измеряется в процентах или долях единицы; первый измеритель используется для вербальной или описательной характеристики финансового актива, второй — при проведении расчетов.

Оценка стоимости облигации без права досрочного погашения выполняется по формуле (5.12); эта же формула, как показано в предыдущем разделе, может использоваться для оценки доходности отзывной облигации. Предполагается, что в формуле (5.12) известны все показатели, кроме r.

Разрешая уравнение относительно г, определяем общую доходность данной облигации. Этот показатель в отечественной финансовой прессе иногда называется доходностью к погашению и обозначается YТМ.

Очевидно, что в общем случае разрешить уравнение (5.12) относительно r можно на компьютере либо на специализированном финансовом калькуляторе. Расчеты вручную возможны, но чрезвычайно затруднены. Кроме того, известна формула, позволяющая получать приблизительную оценку доходности купонной облигации без права досрочного погашения при помощи обычного калькулятора. Этот показатель рассчитывается отношением среднегодового дохода (годовой процент плюс часть разницы между нарицательной стоимостью и ценой покупки облигации) к средней величине инвестиции и дает приблизительную оценку показателя r в формуле (5.12):

где М — номинал облигации;

Р — текущая цена (на момент оценки);

С — купонный доход;

k — число лет, оставшихся до погашения облигации.

Пример. Рассчитать норму дохода облигации нарицательной стоимостью 100 тыс.руб. с годовой купонной ставкой 9%, имеющей текущую рыночную стоимость 84 тыс.руб; облигация будет приниматься через 8 лет.

Решение. По формуле (5.15) имеем:

Таким образом, приблизительная доходность данной облигации составляет 12%.

Источник

13.1.2. Доходность облигации

Проанализируем формулу (13.4), считая, что речь идет об облигации с годовым купонным доходом. В числителе дроби представлен годовой доход, состоящий из купонного дохода (С^) и части капитализированного дохода, приходящейся на один год, оставшийся до погашения, (М — Р0) /т. В знаменателе дроби — среднегодовая инвестиция, рассчитанная как средняя арифметическая из значёний инвестиции соответственно на начало и конец финансовой операции. Таким образом, в модели (13.4) действитёльно представлен показатель эффективности — процентная ставка (в долях единицы), соответствующая длине базисного периода.

Рассчитать доходность облигации Нарицательной стоимостью 1000 руб., с годовой купонной ставкой 9%, имеющей текущую рыночную цену 840 руб.; облигация будет приниматься к погашению через 8 лет.

Соответствующий денежный поток, представленный для наглядности на рис. 13.5, показывает, что в момент времени 0 имеет место отток денежных средств в размере 840 руб. (покупка облигации); в последующие восемь лет держатель облигации будет получать в конце очередного года купонный доход в сумме 90 руб., кроме того, при погашении об

? выплачена держателю облигации в случае досрочного ее погашения, и 2) срока защиты от досрочного погашения (первые т базисных периодов с момента эмиссии, в течение которых отзыв облигации с рынка запрещен). Для подобной облигации можно рассчитать значения доходности на момент ее естественного погашения и на конец т-то базисного периода; все зависит от того, с какой вероятностью инвестор (аналитик) оценивает возможность досрочного погашения.

Доходность конвертируемой облигации. Для оценки ожидаемой доходности конвертируемой облигации можно воспользоваться алгоритмами, используемыми в случае с облигациями с правом досрочного погашения, в которых выкупная цена заменена ожидаемой конверсионной стоимостью. Основным моментом анализа является установление прогнозной оценки стоимости базисного актива на тот или иной момент времени.

Источник

Доходность облигации без права досрочного погашения

Доходность облигаций

В условиях эффективного рынка все облигации одного класса теоретически должны иметь примерно одинаковую доходность.

Доходность облигации без права досрочного погашения в отечественной финансовой прессе иногда называется доходностью к погашению и обозначается YTM по аналогии с англоязычной терминологией (Yield to Maturity, YTM).

Этот показатель рассчитывается отношением среднегодового дохода (годовой процент плюс часть разницы между нарицательной стоимостью и ценой покупки облигации) к средней величине инвестиции и дает приблизительную оценку показателя r в формуле:

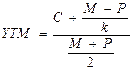где: M – номинал облигации; P – текущая цена (на момент оценки); C – купонный доход; k – число лет, оставшихся до погашения облигации.

Достоинством показателя YTM, как и любого другого показателя эффективности, является возможность использования его в сравнительном анализе при выборе вариантов инвестирования средств в те или иные облигации.

Пример.Рассчитать доходность облигации нарицательной стоимостью 1000 руб. с годовой купонной ставкой 9%, имеющей текущую рыночную цену 840 руб.; облигация будет приниматься к погашению через 8 лет.

Подставляя эти данные в уравнение и разрешая его относительно r, можно найти искомую доходность, равную 12,25%. При отсутствии финансового специализированного калькулятора можно воспользоваться формулой:

Таким образом, доходность данной облигации составляет приблизительно 12%. Видно, что формула обеспечивает достаточную точность расчетов.

В некоторых отечественных пособиях по финансовому анализу для оценки эффективности инвестирования в облигации рекомендуют ориентироваться на показатель текущей или дивидендной доходности (k_d), под которым понимается отношение дохода, получаемого ежегодно по купонной ставке, к фактическим затратам на приобретение облигации:

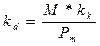где: M – номинал облигации; P_m – текущая цена (на момент оценки); k_k – купонная ставка.

Так, в условиях предыдущего примера текущая доходность облигации составляет:

Показатель текущей доходности облигации не может использоваться в качестве обобщенной характеристики и критерия при анализе целесообразности инвестирования в данные облигации. Он дает искаженную оценку реальной (то есть общей) доходности облигации, поскольку в этом случае не учтен доход ее держателя, полученный от приобретения облигации с дисконтом.

Поэтому более правильным является ориентация на показатель YTM.

Наконец, еще одной характеристикой доходности облигации является показатель купонной доходности, рассчитываемый по следующей формуле:

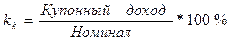Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Доходность облигации без права досрочного погашения

Рт = 2:77 + 777 = CFFM4(r%,n) + MFM2(r%,n), (20.6)

I ‘io CF — сумма регулярно выплачиваемого процентного дохода за базисный период;

п — число базисных периодов до погашения облигации;

М — нарицательная стоимость облигации;

Р,„ — рыночная цена облигации на момент ее приобретения (фактического или условного).

Разрешая уравнение (20.6) относительно г, определяем общую доходность данной облигации. Этот показатель иногда называют доходностью к погашению и обозначают YTM — по аналогии с англоязычной терминологией (Yield to Maturity). Именно этот показатель публикуется обычно в газете «Финансовые известия». Отметим, что в условиях эффективного рынка все облигации одного класса должны иметь примерно одинаковую доходность.

Очевидно, что в общем случае разрешить уравнение (20.6) относительно г можно с помощью компьютера либо финансового калькулятора. Кроме того, известна формула, позволяющая получать приблизительную оценку доходности купонной облигации без права досрочного погашения с помощью обычного калькулятора. Этот показатель рассчитывается отношением среднегодового дохода (годовой процент плюс часть разности нарицательной стоимости и цены покупки облигации) к средней величине инвестиции и дает приблизительную оценку показателя YTM, найденного но формуле (20.6)(20.7)

где С? — купонный доход за базисный период;

А/ — нарицательная стоимость облигации;

т — число базисных периодов, оставшихся до погашения облигации;

Ра — рыночная цена облигации на момент ее приобретения.

Проанализируем формулу (20.7), считая, что речь идет об облигации с годовым купонным доходом. В числителе дроби представлен годовой доход, состоящий из купонного дохода (СО и части капитализированного дохода, приходящейся на один

год, оставшийся до погашения

знаменателе дроби — среднегодовая

инвестиция как средняя арифметическая значений инвестиции соответственно на начало и конец финансовой операции. Имеем показатель эффективности.

Уместно сделать два замечания. Во-первых, формула (20.7) в известном смысле является универсальной и может использоваться, когда базисный период отличен от года. В этом случае т будет выражать число базисных периодов, а ставка, рассчитанная по (20.7), будет выражать ставку за базисный период. Для нахождения показателя УТМ в этом случае надо перейти к годовой ставке (например, если речь идет об облигации с полугодовой выплатой купона, то значение ставки, найденной по формуле (20.7), надо умножить на 2). Во-вторых, в условиях нормально функционирующей экономики, для которой, как известно, не характерны аномально высокие процентные ставки; формула (20.7) дает хорошее приближение.

Достоинством показателя УТМ, как и любого другого показателя эффективности, является возможность использования его в сравнительном анализе (при выборе вариантов инвестирования в те или иные облигации).

Рассчитать доходность облигации нарицательной стоимостью 1000 руб., с годовой купонной ставкой 9%, имеющей текущую рыночную цепу 840 руб. Облигация будет приниматься к погашению через 8 лет.

Соответствующий денежный поток, представленный для наглядности на рис. 20.5, показывает, что в момент временя 0 имеет место отток денежных средств в размере 840 руб. (покупка облигации); в последующие 8 лет держатель облигации будет получать в конце очередного года купонный доход в сумме 90 руб..

90 90 90 90 90 90 90

Рис. 20.5. Денежный поток для срочной купонной облигации

Подставляя эти данные в уравнение (20.6) и решая его относительно г, можно найти доходность, равную 12,25%. При отсутствии финансового с пециал из про ванного калькулятора можно воспользоваться формулой (20.7).

™ = 1000+840 = °’12’ или 12%-

Таким образом, доходность данной облигаиии составляет приблизительно 12%. Видно, что формула (20.7) обеспечивает достаточную точность расчетов.

Еще одной весьма распространенной характеристикой доходности облигации является купонная доходность, рассчитываемая соотнесением купонного дохода к номиналу. На самом деле этот показатель не рассчитывается, а задается в виде купонной ставки. Значимость этого показателя для оценки доходности облигации невысока. Ставка дает оценку доходности облигации лишь в момент ее эмиссии; в дальнейшем она используется для расчета купонного дохода.

Источник

Доходность облигации без права досрочного погашения (синонимы: общая доходность, доходность к погашению)

Оценка стоимости подобной облигации выполняется по формуле (4). Эта же формула может использоваться для оценки доходности отзывной облигации. Предполагается, что в данной формуле известны все показатели кроме r. Разрешая уравнение относительно r, определяем общую доходность данной облигации. Этот показатель в отечественной финансовой прессе называется доходностью к погашению и обозначается YTM (Yield to Maturity).

В общем случае разрешить уравнение (4) относительно r можно лишь с помощью компьютера, либо специализированного финансового калькулятора. Кроме того, известна формула, позволяющая получать приблизительную оценку доходности купонной облигации без права досрочного погашения с помощью обычного калькулятора. Этот показатель рассчитывается отношением среднегодового дохода (годовой процент плюс часть разницы между нарицательной стоимостью и ценой покупки облигации) к средней величине инвестиции и дает приблизительную оценку показателя YTM:

(11)

где M — номинал облигации;

Р — текущая цена (на момент оценки);

С — купонный (регулярный) доход;

k — число лет (базовых периодов), оставшихся до погашения облигации.

Пример. Рассчитать доходность облигации нарицательной стоимостью 1000 руб. с годовой купонной ставкой 9%, имеющей текущую рыночную цену 840 руб.; облигация будет приниматься к погашению через 8 лет.

Соответствующий денежный поток, представленный для наглядности на рис.6, показывает, что в момент времени 0 имеет место отток денеж­ных средств в размере 840 руб.; в последующие восемь лет держатель об­лигации будет получать в конце каждого очередного года купонный доход в сумме 90 руб. (1000 х 9%), кроме того, при погашении облигации он получит еще 1000 руб.

Рис. 6. Денежный поток для срочной купонной облигации

Подставляя эти данные в уравнение (4) и разрешая его относи­тельно r, можно найти искомую доходность, равную 12,25%. При от­сутствии финансового специализированного калькулятора можно вос­пользоваться формулой (11):

YTM = [90+ (1000-840)/ 8] / [(1000 + 840)/ 2 = 0,1196 или 11,96%.

Таким образом, доходность данной облигации составляет прибли­зительно 12%. Видно, что формула (11) обеспечивает достаточную точность расчетов.

Часто для оценки эффективности инвестирования в облигации рекомендуется ориентироваться на показатель текущей, или дивидендной, доходнос­ти (k_d), под которым понимается отношение дохода, получаемого еже­годно по купонной ставке, к фактическим затратам на приобретение облигации:

М х k_к / Рm (12)

где М — номинальная стоимость облигации;

Рт — текущая рыночная цена облигации;

kк — купонная ставка, %.

Так, в условиях предыдущего примера текущая доходность облига­ции составляет:

k_d = 1000 х 9% / 840 = 10,7% .

Из формулы (12) видно, что показатель текущей доходности не может использоваться в качестве обобщенной характеристики и кри­терия при анализе целесообразности инвестирования в данные об­лигации. Он дает искаженную оценку реальной (т.е. общей) доход­ности облигации, поскольку в этом случае не учтен доход ее держа­теля, полученный от приобретения облигации с дисконтом. Поэтому более правильным является ориентация на показатель YTM.

Наконец еще одной характеристикой доходности облигации явля­ется показатель купонной доходности, рассчитываемый по следую­щей формуле:

Kк = Купонный доход / Номинал (13)

Чаще всего этот показатель не рассчитывается, а задается в виде купонной ставки. Значимость этого показателя для оценки доходнос­ти облигации невысока: эта ставка дает оценку доходности облигации лишь в момент ее эмиссии; в дальнейшем она использует­ся в основном для расчета купонного дохода.

Источник