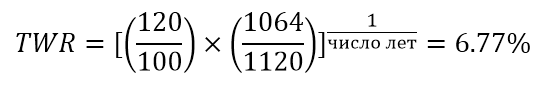Доходность mwr что это

Реальная доходность портфеля: расчет и смысл

Некоторое время назад я писал статью о расчете рыночной доходности. Статья несомненно важная и рекомендуется всем, кто имеет дело с инвестициями, поскольку очень многие считают доходность либо неправильно (обычно новички, в частности путая среднеарифметические и среднегеометрические данные), либо намеренно завышают результат (обычно инвестиционные фонды, экстраполируя удачные квартальные показатели в будущее).

Тем не менее у приведенных расчетов есть недостаток. Дело в том, что разовое инвестирование одной суммы (без промежуточных вводов и выводов до выхода из рынка) это скорее гипотетический подход. Даже если не брать во внимание купонные выплаты и дивиденды, которые не всегда могут быть сразу же реинвестированы, реальное инвестирование предполагает периодические вводы и выводы средств, что плохо вписывается в представленные по ссылке формулы.

Два вида доходности: TWR и MWR

Представим такую ситуацию. Мы инвестировали в рынок 100 долларов, которые за год выросли на 20%. Соответственно, у нас на счету оказалось $120. Довольные результатом, мы вносим теперь 1000 долларов. Однако рынок ведет себя иначе: на следующий год он падает на 5%. Следовательно, наша конечная сумма оказывается равна 1120 × (1 – 0.05) = $1064. А как подсчитать полученную доходность?

В этом случае есть два способа:

• TWR (Time Weighted Return / доходность, взвешенная по времени)
• MWR (Money Weighted Retutn / доходность, взвешенная по деньгам)

Разберемся с ними отдельно.

1. TWR

Считается более традиционной, хотя это можно оспорить. Для ее расчета инвестиционный процесс разбивается на интервалы, в которых происходят ввод или вывод средств, таким образом нивелируя их влияние на результат. В нашем случае инвестиции разбиты на два равных годовых отрезка (число лет =2):

Фактически TWR отражает доходность неизменной суммы инвестора с начала инвестиций без пополнений и снятий. Но насколько логичен этот результат у нас? На первом отрезке мы заработали $20, однако на втором потеряли 1064 – 1120 = $56. Т.е. фактически у нас убыток, вызванный многократным увеличением вклада при последующем снижении рынка, а TWR считает нам плюс, игнорируя абсолютное значение взноса.

2. MWR

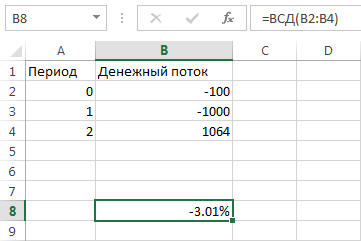
Учесть этот недостаток TWR может доходность, взвешенная по деньгам. Она отражает движение денежных средств и может быть посчитана при помощи функции ВСД в Excel. Для этого нам нужны вносимые средства со знаком «минус» и конечный результат на счете. Для случая выше расчет следующий:

Итого, MWR = – √1 + (3.01%/100%) = –1.49%. Корень означает степень ½, где 2 — число лет инвестиций. Как видно, доходность по деньгам более адекватно описывает поведение нашего реального счета, хотя для ее вычисления мы прописываем только ввод средств и конечный результат. MWR и TWR встречаются в аналитике зарубежных брокеров и в сервисах расчета инвестиционных портфелей.

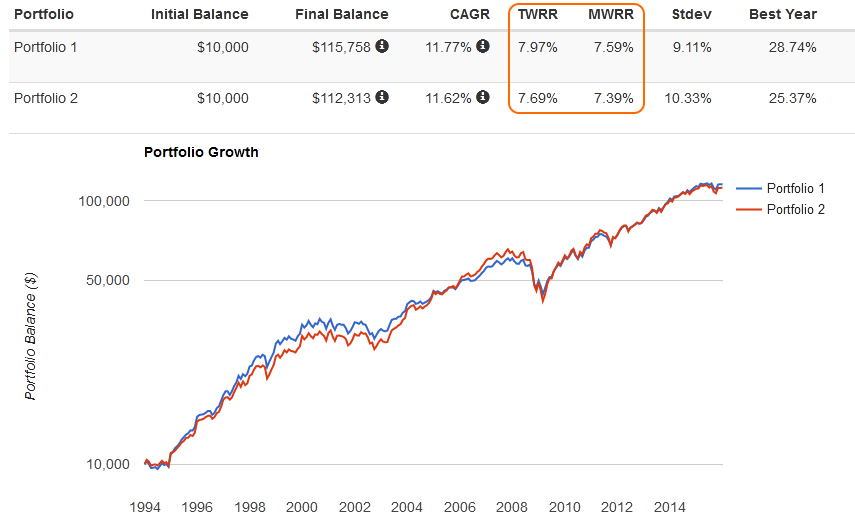
CAGR (Compound Annual Growth Rate) в данном случае включает в результат все вносимые инвестором средства (ежегодно $1000), не отделяя их от рыночной доходности – поэтому результат получается заметно лучше.

Итоги

Наша ситуация вполне могла быть обратной: вначале мы получаем заметный минус на малую сумму, затем вносим гораздо больше и фиксируем небольшой плюс. Нетрудно рассчитать, что тогда TWR будет отрицательной, а MWR положительной. Можно сказать, что TWR описывает стратегию инвестора в целом, тогда как MWR включает в нее движения средств — таким образом, удачно влив крупную сумму перед периодом роста можно заметно улучшить доходность стратегии. И наоборот.

Учет инвестиций с помощью ЧИСТВНДОХ

Проблема функции ВСД в том, что она верна для периодических денежных потоков, поступающих и/или убывающих через равные промежутки времени. Однако понятно, что в реальных инвестициях ввод/вывод средств обычно происходит в спонтанном режиме. В этом случае для расчета доходности портфеля можно воспользоваться функцией ЧИСТВНДОХ.

Вся подобная статистика должна содержаться в брокерском отчете. Вычисления выполняются с помощью итерационного метода, подробное описание функции можно найти здесь .

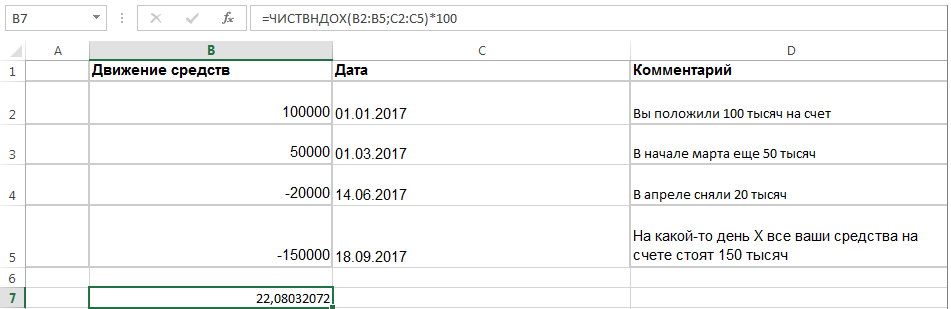
Основными в расчете являются две колонки: значений (введенных и выведенных средств) и соответствующих дат, когда происходил ввод или вывод денег. Обратите внимание, что общая стоимость активов указывается со знаком минус. После чего в произвольную ячейку, где требуется результат, нужно ставить следующую формулу:

В2:B5 — диапазон ячеек со значениями введенных или выведенных средств

С2:С5 — диапазон ячеек с датами, когда происходил ввод или вывод

Умножение на 100 позволяет получить результат в процентах. Для примера выше средняя годовая доходность будет ≈ 22.1%.

🔔 При инвестициях меньше года подобный расчет является некорректным. Кроме того, поскольку на рынке периодически возникают пузыри (доткомов на рынке США в 1995-2000 годах или российских активов на росте нефти в 2000-2008), а также бывают затяжные кризисы (обычно именно после пузырей — например Великая Депрессия 30-х или Япония после 1990 года), то для более адекватной оценки портфеля гораздо лучше подходят временные интервалы в несколько лет, чем за 1-2 года.

В заключении пример доходности инвестиционного портфеля одного моего клиента:

Источник

Ставка доходности, взвешенная по деньгам

Что такое Ставка доходности, взвешенная по деньгам?

Ставка доходности, взвешенная в денежном выражении (MWRR), является показателем эффективности инвестиций. MWRR рассчитывается путем нахождения нормы прибыли, которая устанавливает текущие значения всех денежных потоков, равные стоимости первоначальных инвестиций. MWRR эквивалентен внутренней норме доходности (IRR).

Ключевые моменты:

• Ставка доходности, взвешенная по денежным средствам (MWRR), является показателем эффективности инвестиций.
• MWR рассчитывается путем нахождения нормы прибыли, которая устанавливает текущие значения всех денежных потоков, равные стоимости первоначальных инвестиций.
• Ставка доходности, взвешенная в денежном выражении, эквивалентна внутренней норме доходности.
• MWR устанавливает начальную стоимость инвестиции, равную будущим денежным потокам, таким как добавленные дивиденды, снятие средств, депозиты и выручка от продажи.

Понимание нормы прибыли, взвешенной по деньгам

Формула для MWRR Is

пVОзнак равнопVязнак равноCF0+CF1(1+ярр)+CF2(1+ярр)2+CF3(1+ярр)3+…CFп(1+ярр)пжчере:пVОзнак равноPV OutflowsпVязнак равноPV InflowsCF0знак равноЯпятялсычоутлуогянvEсектмент CF1,CF2,CF3,…CFпзнак равноCAсекч еложеNзнак равноEach periodяррзнак равноИнитиал рате оф ретурн\begin &PVO = PVI = CF_ <0>\, +\, \frac><(1\, +\, IRR)>\, +\, \frac><(1\, +\, IRR)^<2>>\,\\ &\qquad\quad\, +\, \frac><(1\, +\, IRR)^<3>>\,\, +\,… \frac><(1\, +\, IRR)^>\,\\ &\textbf\\ &PVO = \text\\ &PVI = \text\\ &CF_0 = \text\\ &CF_1, CF_2, CF_3, … CF_n = \text\\ &N = \text\\ &IRR = \text\\ \end​PVO=PVI=CF0​+(1+IRR)

How to Calculate the Money-Weighted Rate of Return

1. To calculate IRR using the formula, set net present value equal to zero and solve for the discount rate (r), which is the IRR.
2. However, because of the nature of the formula, IRR cannot be calculated analytically and must instead be calculated either through trial and error or using software programmed to calculate IRR.

What Does the Money-Weighted Rate of Return Tell You?

There are many ways to measure asset returns, and it is important to know which method is being used when reviewing asset performance. The MWRR incorporates the size and timing of cash flows, so it is an effective measure of portfolio returns.

The MWRR sets the initial value of an investment to equal the future cash flows, such as dividends added, withdrawals, deposits, and sale proceeds. In other words, the MWRR helps determine the rate of return needed to start with the initial investment amount factoring all of the changes to cash flows during the investment period including the sale proceeds.

Cash Flows and the Money-Weighted Rate of Return

As stated earlier, the MWRR for an investment is identical in concept to the IRR. In other words, it is the discount rate on which the net present value (NPV) = 0, or the present value of inflows = present value of outflows.

It’s important to identify the cash flows in and out of a portfolio including the sale of the asset or investment. Some of the cash flows that an investor might have in a portfolio include:

Outflows

• The cost of any investment purchased
• Reinvested dividends or interest
• Withdrawals

Inflows

• The proceeds from any investment sold
• Dividends or interest received
• Contributions

Example of the Money-Weighted Rate of Return

Each inflow or outflow must be discounted back to the present using a rate (r) that will make PV (inflows) = PV (outflows).

Let’s say an investor buys one share of a stock for $50 that pays an annual $2 dividend and sells it after two years for $65. The MWRR will be a rate that satisfies the following equation:

PV Outflows=PV Inflows=$21 + r + $2(1 + r)2 + $65(1 + r)3=$50\begin &PV \text< Outflows>\\ &\qquad= PV \text < Inflows>= \frac<\$2><1\ +\ r>\ +\ \frac<\$2><(1\ +\ r)^2>\ +\ \frac<\$65><(1\ +\ r)^3>\\ &\qquad= \$50 \end​PV Outflows=PV Inflows=1 + r

Solving for r using a spreadsheet or financial calculator, we have an MWRR of 11.73%.

The Difference Between Money-Weighted Rate of Return and Time-Weighted Rate of Return

The money-weighted rate of return is often compared to the time-weighted rate of return (TWRR), but the two calculations have distinct differences. The TWRR is a measure of the compound rate of growth in a portfolio. The TWRR measure is often used to compare the returns of investment managers because it eliminates the distorting effects on growth rates created by inflows and outflows of money.

It can be difficult to determine how much money was earned on a portfolio because deposits and withdrawals distort the value of the return on the portfolio. Investors can’t simply subtract the beginning balance, after the initial deposit, from the ending balance since the ending balance reflects both the rate of return on the investments and any deposits or withdrawals during the time invested in the fund.

The TWRR breaks up the return on an investment portfolio into separate intervals based on whether money was added or withdrawn from the fund. The MWRR differs in that it takes into account investor behavior via the impact of fund inflows and outflows on performance but doesn’t separate the intervals where cash flows occurred like the TWRR. Therefore, cash outlays or inflows can impact the MWRR. If there are no cash flows, then both methods should deliver the same or similar results.

Limitations of Using Money-Weighted Rate of Return

The MWRR considers all the cash flows from the fund or contribution, including withdrawals. Should an investment extend over several quarters, for example, the MWRR lends more weight to the performance of the fund when it is at its largest. Hence, the description “money-weighted.”

The weighting can penalize fund managers because of cash flows over which they have no control. In other words, if an investor adds a large sum of money to a portfolio just before its performance rises, it equates to positive action. This is because the larger portfolio benefits more (in dollar terms) from the growth of the portfolio than if the contribution had not been made.

On the other hand, if an investor withdraws funds from a portfolio just prior to a surge in performance, it equates to a negative action. The now-smaller fund sees less benefit (in dollar terms) from the growth of the portfolio than if the withdrawal had not occurred.

Источник

Требуемая доходность | Required Rate of Return

Прибыль и доходность ценных бумаг

Определение 1
Доходность ценных бумаг представляет собой относительный показатель эффективности от капиталовложений, выражающий отношение годового дохода компаний к рыночной цене акций.

В соответствии с видами ценных бумаг, финансовых инструментов и системы подсчета принято различать несколько разновидностей доходности:

• Внутренняя норма, представляющая собой процентную ставку, которую рассчитывают на основе расчета потока платежей, учитывая временной фактор.
• Годовая процентная доходность или сложный процент за год, который условно начисляется один раз и выражается в доходной ставке.
• Доходность к погашению, выражающая внутреннюю доходность удержания долговых ценных бумаг до момента полного их погашения.
• Текущая доходность ценной бумаги, используемая очень редко по причине ряда недостатков.

Готовые работы на аналогичную тему

• Курсовая работа Прибыль ценных бумаг 450 руб.
• Реферат Прибыль ценных бумаг 220 руб.
• Контрольная работа Прибыль ценных бумаг 220 руб.

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

5.3. Требуемая доходность инвестиций

Г.Я. Гольдштейн, А. Н. Гуц Экономический инструментарий принятия управленческих решений

Учебное пособие для магистрантов направления 521500 «Менеджмент» (МВА). Таганрог: ТРТУ, 1999

Предыдущая

Оглавление

Следующая

5. ОСНОВЫ РИСК-МЕНЕДЖМЕНТА

Соединение концепций рыночной линии и кривых индифферентности позволяет определить точку оптимальной инвестиции для данного инвестора. При поиске инвестиционных возможностей потенциальный инвестор движется, как правило, от поиска высокой доходности к компромиссу между тем, что ему хотелось бы, к тому, что предлагает рынок, то есть от кривых индифферентности, расположенных выше, к тем, которые пониже. Приемлемой инвестицией является точка, которая одновременно имеется на рынке и принадлежит к одной из кривых индифферентности на разных уровнях ожидания инвестора. Оптимальной точкой является точка касания кривой индифферентности и самой верхней из альтернатив, предлагаемых рынком, как это показано на рис.5

Рис.5. Кривые индифферентности и рыночная линия

Теперь у нас есть теоретическая база для рассмотрения требуемой прибыльности инвестиции. Сначала определяется уровень риска, потом – уровень доходности. И наконец, сводя их вместе, инвестор получает возможность оптимизировать рост рискованности с ростом доходности. Этот подход все еще не является общепринятым. Многие, инвесторы пользуются средневзвешенной стоимостью долга и капитала

. Далее будут рассмотрены и сравнены все три подхода.

СТРУКТУРА И СТОИМОСТЬ КАПИТАЛА

Структура капитала фирмы может быть определена как смесь заемных фондов и паевого капитала, используемая для финансирования ее активов. Иногда краткосрочные заимствования исключаются из капитала. Однако, если краткосрочные заимствования осуществляются на постоянной основе, как ролловерный (автоматически возобновляемый на новый строк) кредит, его можно включить в состав капитала при анализе структуры финансирования, что мы и делаем в дальнейшем изложении.

Под стоимостью капитала (синоним – средневзвешенная требуемая доходность, СТД) понимается ставка доходности, которую требует инвестор на свой инвестированный капитал. Средневзвешенная стоимость капитала – это методика измерения требуемой доходности по каждой компоненте капитала фирмы в отдельности. Стоимость каждой компоненты заемного капитала и величина дохода каждой составляющей собственного капитала по отдельности умножается на свой весовой коэффициент. Затем взвешенные таким образом компоненты складываются, образуя совокупный требуемый доход, которого достаточно для обслуживания долга, выплаты дивидендов держателям привилегированных акций и достаточной компенсации держателям простых акций за то, что они принимают на себя риск.

Етр=Дрын Кi (1-Нк)+ПрынКпа+ОрынКд

где Етр – совокупная требуемая доходность фирмы; Кi – доналоговая стоимость долга; Нк – ставка корпоративного налога фирмы; Кпа – требуемая ставка доходности привилегированных акций; Кд – требуемая ставка доходности обычных акций;

Дрын, Прын, Орын – процентные доли долга, привилегированных акций и обыкновенных акций в капитале фирмы по текущим рыночным ценам, соответственно.

Рассмотрим фирму с 15 млн. руб. долга под 14%, 10 млн. руб. привилегированных акций с доходностью 15% и 4,5 млн. обычных акций с текущей рыночной стоимостью по 20 руб. за акцию. Текущая доходность обычных акций составляет 17% и корпоративная ставка налога на фирму равна 40%. Какова СТД фирмы?

Для вычисления структуры капитала фирмы нужно знать суммарную стоимость фирмы. В данном случае ее можно подсчитать как сумму:

Vрын= Дрын+ Прын+ Орын,

где Vрын — суммарная стоимость фирмы на рынке,

Дрын, Прын, Орын — рыночная стоимость долга, привилегированных акций и обыкновенных акций, соответственно.

В нашем примере

Vрын = 15 000 000 + 10 000 000 + 4 500 000 . 20 = 115 000 000 рублей.

Средневзвешенная требуемая доходность фирмы будет равна:

Етр=15 000:115 000 . 0,14 . (1-0,40)+10 000:115 000 . 0,15+

+90 000:115 000 . 0,17=0,157.

Формула СТД дает величину требуемой совокупной доходности при известной структуре капитала фирмы. Расчет стоимости и доходности каждой компоненты капитала в отдельности (долга, привилегированных и обычных акций) будут рассмотрены ниже.

В большинстве случаев стоимость доли фирмы известна. В западной практике для получения стоимости долга этой или аналогичной фирмы используются данные газеты Wall Street Journal, бюро кредитного рейтинга Dun & Bradstreet, компьютерного информационного агентства Bloomberg, Интернет и других подобных весьма многочисленных источников. В российской современной практике эти источники становятся все более доступными и содержательными. Например, Dun & Bradstreet уже давно имеет офис в Москве, Интернет доступен практически всем квалифицированным людям. Стоимость своего заемного капитала фирма может уточнить со своим банком. Для расчета СТД требуется знать эффективную стоимость долга, которая определяется как фактическая стоимость с учетом всех релевантных факторов. В основном требуется сделать два уточнения величины простой банковской ставки:

1. Рыночные, а не бухгалтерские стоимости. В балансе бухгалтеры указывают стоимости по номиналу, а рынок дает свои колеблющиеся котировки на все элементы капитала, в том числе и на банковский процент.

2. Чистые поступления. Новый заем приносит меньше денег, чем его номинал, потому что самооформление нового займа стоит денег. Это значит, что новый долг с такой же процентной ставкой стоит дороже старого долга. Для вычисления эффективной стоимости долга нужно учитывать лишь фактические, а не номинальные поступления денег.

Для вычисления эффективной стоимости заемного капитала фирмы используется формула:

Кi = (Суммарные годовые процентные платежи) : Дрын.

Рассмотрим фирму со следующими составляющими заемного капитала:

Вид заимствования	Годовая стоимость	Балансовая стоимость в рублях	Рыночная стоимость или чистые поступления в рублях
Счета к оплате	0	8 500 000	8 500 000
Краткосрочные обязательства	0,150	4 000 000	4 000 000
Долгосрочные облигации	0,145	15 000 000	13 000 000
Новые долгосрочные займы	0,162*	6 000 000	31 000 000

*Годовая стоимость нового займа рассчитывается по формуле, которая амортизирует выпускные комиссионные за весь жизненный период долга. В данном случае мы не рассматриваем эту методику, но читатель должен осознавать, что стоимость нового займа включает стоимость выпуска нового займа.

Если фирма продержит точно такую структуру заемного капитала в течение года, то ей придется заплатить годовые процентные платежи в сумме 3747000 рублей:

8500000 . 0 + 4000000 . 0,150 + 15000000 . 0,145 + 6000000 . 0,162 =

Разделив эту сумму на рыночную стоимость долга, получим доналоговую стоимость заемного капитала в 12,1% годовых:

Кi = 3747000 : 31000000 = 0,121.

ТРЕБУЕМАЯ ДОХОДНОСТЬ ПРИВИЛЕГИРОВАННОЙ АКЦИИ

Требуемая доходность привилегированной акции рассчитывается подобно стоимости долга:

Кпа = Дивиденд / Рыночная стоимость акции = 100 . 0,15 : 120 = 0,117.

ТРЕБУЕМАЯ ДОХОДНОСТЬ ПРОСТОЙ АКЦИИ

Поскольку покупатель простой акции рассчитывает не на фиксированный доход, а на долю в успехах фирмы, оценить доходность этой ценной бумаги сложно.

Прежде всего необходимо определиться, с какой точки зрения проводится оценка прибыльности – с позиций продолжающегося бизнеса (а going concern) или с позиций ликвидации бизнеса (liquidation value). Для pacчета прибыльности следует соотнести сегодняшнюю стоимость будущих денежных потоков, генерируемых акцией, и сегодняшнюю требуемую стоимость акции (Ке):

Ке = Заработки на акцию / Рыночная цена акции.

Теоретически понятно, что рыночная цена, в принципе, равна сегодняшней стоимости всех дивидендов, которые поступят на акцию от сегодняшнего дня по бесконечности:

Рцпа=PV(div1 + div2 + div3 + … + divn).

Как можно оценить бесконечный денежный поток дивидендов? Можно предположить, что дивиденды будут постоянно расти с постоянной ставкой, которая, как можно предположить, будет расти пропорционально удержанной прибыли:

где g – ставка роста дивидендов;

Да — доход на одну акцию;

Ц рпа– рыночная цена простой акции;

Пу – поля удержанной прибыли в чистой прибыли компании.

При этом подходе не учитываются продажи новых акций и новые заимствования.

В начале 60-х годов американский ученый Майрон Гордон разработал модель оценки стоимости акций /12 /.

Црпа = divтек /(Ке — g),

где divтек – текущая ставка дивидендов.

Формула не противоречит здравому смыслу: акционер либо получает дивиденды, придерживая рост фирмы и стоимость обыкновенных акций; либо позволяет фирме расти за счет удержанной прибыли и таким образом увеличивать стоимость акций. Но это справедливо лишь для теоретического предположения, что темп роста фирмы соответствует доле удержанной прибыли. Увы, это не всегда так.

КАК ОПРЕДЕЛЯТЬ ТРЕБУЕМУЮ ДОХОДНОСТЬ

Подводя итог рассмотренным в данной главе методикам, можно предложить рассчитывать приемлемую величину требуемой ставки доходности (в процентах) как средневзвешенную величину трех компонент:

– стоимости долга (Кi) (взвешенной на долю заемного капитала в обязательствах фирмы);

– взвешенной на соответствующую долю стоимости привилегированных акций (Кпа );

– взвешенную доходность обыкновенных акций (Ке).

Эта методика дает удовлетворительные результаты при нормальных уровнях доходности, что характерно для большинства фирм. Она проста и логична. Она неплохо отражает перемены в структуре обязательств фирмы. При умеренном заимствовании она также дает хорошие результаты.

Эта модель не пригодна: – при сильных отклонениях структуры капитала или доходности фирмы от среднерыночных значений, что характерно для оригинальных бизнесов и венчурных проектов; – при сильных отклонениях риска проекта от умеренных.

Концепция требуемой доходности чрезвычайно важна при принятии финансовых решений. Можно применять ту или иную теоретическую модель, однако лицам, принимающим решения, следует ориентироваться не только на расчеты по формулам или среднеотраслевые значения. Этот жизненно важный для фирмы показатель следует уточнять, уточнять и уточнять… От того, насколько удачно он будет выбран, зависит не ввяжется ли фирма в убыточную аферу, или не упустит ли она свой шанс.

Предыдущая

Оглавление

Следующая

Реальная доходность портфеля: расчет и смысл

Некоторое время назад я писал статью о расчете рыночной доходности. Статья несомненно важная и рекомендуется всем, кто имеет дело с инвестициями, поскольку очень многие считают доходность либо неправильно (обычно новички, в частности путая среднеарифметические и среднегеометрические данные), либо намеренно завышают результат (обычно инвестиционные фонды, экстраполируя удачные квартальные показатели в будущее).
Тем не менее у приведенных расчетов есть недостаток. Дело в том, что разовое инвестирование одной суммы (без промежуточных вводов и выводов до выхода из рынка) это скорее гипотетический подход. Даже если не брать во внимание купонные выплаты и дивиденды, которые не всегда могут быть сразу же реинвестированы, реальное инвестирование предполагает периодические вводы и выводы средств, что плохо вписывается в представленные по ссылке формулы.

Два вида доходности: TWR и MWR

Представим такую ситуацию. Мы инвестировали в рынок 100 долларов, которые за год выросли на 20%. Соответственно, у нас на счету оказалось $120. Довольные результатом, мы вносим теперь 1000 долларов. Однако рынок ведет себя иначе: на следующий год он падает на 5%. Следовательно, наша конечная сумма оказывается равна 1120 × (1 – 0.05) = $1064. А как подсчитать полученную доходность?

В этом случае есть два способа:

• TWR (Time Weighted Return
  / доходность, взвешенная по времени)
• MWR (Money Weighted Retutn
  / доходность, взвешенная по деньгам)

Разберемся с ними отдельно.

Считается более традиционной, хотя это можно оспорить. Для ее расчета инвестиционный процесс разбивается на интервалы, в которых происходят ввод или вывод средств, таким образом нивелируя их влияние на результат. В нашем случае инвестиции разбиты на два равных годовых отрезка (число лет =2):

Фактически TWR отражает доходность неизменной суммы инвестора с начала инвестиций без пополнений и снятий. Но насколько логичен этот результат у нас? На первом отрезке мы заработали $20, однако на втором потеряли 1064 – 1120 = $56. Т.е. фактически у нас убыток, вызванный многократным увеличением вклада при последующем снижении рынка, а TWR считает нам плюс, игнорируя абсолютное значение взноса.

Учесть этот недостаток TWR может доходность, взвешенная по деньгам. Она отражает движение денежных средств и может быть посчитана при помощи функции ВСД в Excel. Для этого нам нужны вносимые средства со знаком «минус» и конечный результат на счете. Для случая выше расчет следующий:

Итого, MWR = – √1 + (3.01%/100%) = –1.49%. Корень означает степень ½, где 2 — число лет инвестиций. Как видно, доходность по деньгам более адекватно описывает поведение нашего реального счета, хотя для ее вычисления мы прописываем только ввод средств и конечный результат. MWR и TWR встречаются в аналитике зарубежных брокеров и в сервисах расчета инвестиционных портфелей.

CAGR (Compound Annual Growth Rate) в данном случае включает в результат все вносимые инвестором средства (ежегодно $1000), не отделяя их от рыночной доходности – поэтому результат получается заметно лучше.

Итоги

Наша ситуация вполне могла быть обратной: вначале мы получаем заметный минус на малую сумму, затем вносим гораздо больше и фиксируем небольшой плюс. Нетрудно рассчитать, что тогда TWR будет отрицательной, а MWR положительной. Можно сказать, что TWR описывает стратегию инвестора в целом, тогда как MWR включает в нее движения средств — таким образом, удачно влив крупную сумму перед периодом роста можно заметно улучшить доходность стратегии. И наоборот.

Учет инвестиций с помощью ЧИСТВНДОХ

Проблема функции ВСД в том, что она верна для периодических денежных потоков, поступающих и/или убывающих через равные промежутки времени. Однако понятно, что в реальных инвестициях ввод/вывод средств обычно происходит в спонтанном режиме. В этом случае для расчета доходности портфеля можно воспользоваться функцией ЧИСТВНДОХ.

Вся подобная статистика должна содержаться в брокерском отчете. Вычисления выполняются с помощью итерационного метода, подробное описание функции можно найти здесь.

Основными в расчете являются две колонки: значений (введенных и выведенных средств) и соответствующих дат, когда происходил ввод или вывод денег. Обратите внимание, что общая стоимость активов указывается со знаком минус. После чего в произвольную ячейку, где требуется результат, нужно ставить следующую формулу:

В2:B5 — диапазон ячеек со значениями введенных или выведенных средств

С2:С5 — диапазон ячеек с датами, когда происходил ввод или вывод

Умножение на 100 позволяет получить результат в процентах. Для примера выше средняя годовая доходность будет ≈ 22.1%.

Источник