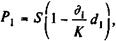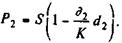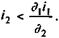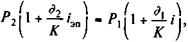Доходность купли-продажи финансовых инструментов
Краткосрочные финансовые инструменты денежно-кредитного рынка — векселя, тратты, различные депозитные сертификаты и т.д. — могут быть проданы до наступления срока их оплаты. Владелец при этом получает некоторый доход, а в неблагоприятных условиях несет убытки.
Покупка и продажа векселя (простая учетная ставка). Если вексель или другой вид долгового обязательства через некоторое время после его покупки и до наступления срока погашения продан, то эффективность этой операции можно измерить в виде простых или сложных процентов. Финансовая результативность операции здесь связана с разностью цен купли-продажи, которые в свою очередь определяются сроками этих актов до погашения векселя и уровнем учетных ставок. Покажем это. Пусть номинал векселяравен S руб. Он был куплен (учтен) по учетной ставке d1 за 
Цена в момент покупки составила
где K — временная база учета.
За 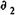
Инвестиции в начале операции составили, таким образом, P1 руб., отдача от них P2 руб. Операция продолжалась 

Отсюда доходность купли-продажи векселя (в виде ставки простых процентов)

Выразив p1 и P2 через определяющие эти величины параметры, находим

Для того чтобы операция не была убыточной, необходимо, чтобы

Заменив в формуле (9.11) P2 и P1 на адекватные выражения, находим

Очевидно, что реальная доходность (т.е. когда iЭ > 1), как и в случае с простыми процентами, будет иметь место, если 
а) покупается по номиналу, продается за 
б) покупается после выпуска и погашается в конце срока;
в) покупается и продается в пределах объявленного срока.
Для варианта а получим знакомое равенство (9.7):

однако символы здесь имеют другое содержание, а именно: Р1 — номинал, P2 — цена продажи, 
Доходность владения сертификатом в течение 

В случае когда измерителем эффективности выступает сложная процентная ставка и заданы цены, получим формулу, аналогичную (9.11). Если расчет основан на уровнях процентных ставок, то

Отметим, что доходность операции имеет место только в том случае, когда 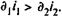
Перейдем теперь к варианту б. Здесь справедливо равенство
i —объявленная процентная ставка.
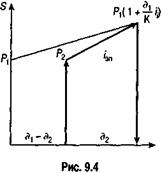
Контур для данного уравнения приведен на рис. 9.4. Из приведенного равенства получим значение iЭП при заданной величине P2:

Если в качестве измерителя эффективности принята ставка сложных процентов, то

Рассмотрим вариант в. Здесь покупка производится спустя некоторое время после выпуска сертификата, а его продажа — до момента погашения. В этом случае опять приходим к уравнению (9.7), в котором P1 означает цену приобретения (а не номинал). Отсюда для расчета iЭП и iЭ пригодны формулы (9.8) — (9.11).
Как видим, на величины iЭП и iЭ в вариантах а, в влияют как срок владения инструментом, так и колебания процентных ставок.
Пример 9.6. Операция заключается в покупке сертификата за 1020 тыс. руб. за 160 дней до его выкупа. Инструмент был продан за 1060 тыс. руб. через 90 дней. Какова доходность операции, измеренная в виде простой и сложной ставок? Исходные данные: Р1 = 1020, P2 = 1060, 


Пусть временная база простых процентов равна 365 дням, тогда по формуле (9.8) находим
iЭП = 
iЭ = 
Величину iЭ можно определить и непосредственно по формуле (9.11):
iЭ = 
Пример 9.7. Финансовый инструмент, приносящий постоянный процент, куплен за 200 дней до срока его погашения и продан через 100 дней. В момент покупки процентная ставка на рынке была равна 10%, в момент продажи — 9,8%. Доходность операции купли-продажи в виде годовой ставки сложных процентов равна согласно (9.14)
iЭ = 
Пример 9.8. Сертификат с номиналом 100 тыс. руб. с объявленной доходностью 12% годовых (простые проценты) сроком 720 дней куплен за 110 тыс. руб. за 240 дней до его оплаты. Какова доходность инвестиций в виде iЭ?
Если K = 360 дней, то по формуле (9.16) получим
iЭ = 
Источник
Доходность купли-продажи финансовых инструментов
Краткосрочные финансовые инструменты денежно-кредитного рынка — векселя, тратты, различные депозитные сертификаты и т.д. — могут быть проданы до наступления срока их оплаты. Владелец при этом получает некоторый доход, а в неблагоприятных условиях несет убытки.
Покупка и продажа векселя (простая учетная ставка). Если вексель или другой вид долгового обязательства через некоторое время после его покупки и до наступления срока погашения продан, то эффективность этой операции можно измерить в виде простых или сложных процентов. Финансовая результативность операции здесь связана с разностью цен купли-продажи, которые в свою очередь определяются сроками этих актов до погашения векселя и уровнем учетных ставок. Покажем это. Пусть номинал векселяравен S руб. Он был куплен (учтен) по учетной ставке d1 за 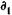
Цена в момент покупки составила
где K — временная база учета.
За 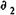
Инвестиции в начале операции составили, таким образом, P1 руб., отдача от них P2 руб. Операция продолжалась 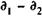
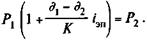
Отсюда доходность купли-продажи векселя (в виде ставки простых процентов)
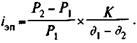
Выразив p1 и P2 через определяющие эти величины параметры, находим

Для того чтобы операция не была убыточной, необходимо, чтобы
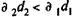
Заменив в формуле (9.11) P2 и P1 на адекватные выражения, находим

Очевидно, что реальная доходность (т.е. когда iЭ > 1), как и в случае с простыми процентами, будет иметь место, если 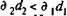
Обратимся к наиболее распространенному виду сертификата — с разовой выплатой процентов — и рассмотрим три возможных варианта операции купли-продажи этого инструмента по срокам:
а) покупается по номиналу, продается за 
б) покупается после выпуска и погашается в конце срока;
в) покупается и продается в пределах объявленного срока.
Для варианта а получим знакомое равенство (9.7):
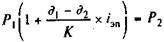
однако символы здесь имеют другое содержание, а именно: Р1 — номинал, P2 — цена продажи, 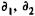
Доходность владения сертификатом в течение 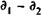
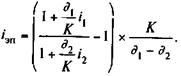
В случае когда измерителем эффективности выступает сложная процентная ставка и заданы цены, получим формулу, аналогичную (9.11). Если расчет основан на уровнях процентных ставок, то
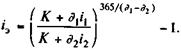
Отметим, что доходность операции имеет место только в том случае, когда 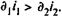
Перейдем теперь к варианту б. Здесь справедливо равенство
i —объявленная процентная ставка.
Контур для данного уравнения приведен на рис. 9.4. Из приведенного равенства получим значение iЭП при заданной величине P2:

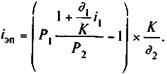
Если в качестве измерителя эффективности принята ставка сложных процентов, то
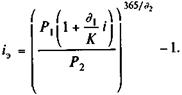
Рассмотрим вариант в. Здесь покупка производится спустя некоторое время после выпуска сертификата, а его продажа — до момента погашения. В этом случае опять приходим к уравнению (9.7), в котором P1 означает цену приобретения (а не номинал). Отсюда для расчета iЭП и iЭ пригодны формулы (9.8) — (9.11).
Как видим, на величины iЭП и iЭ в вариантах а, в влияют как срок владения инструментом, так и колебания процентных ставок.
Пример 9.6. Операция заключается в покупке сертификата за 1020 тыс. руб. за 160 дней до его выкупа. Инструмент был продан за 1060 тыс. руб. через 90 дней. Какова доходность операции, измеренная в виде простой и сложной ставок? Исходные данные: Р1 = 1020, P2 = 1060, 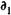
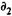
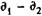
Пусть временная база простых процентов равна 365 дням, тогда по формуле (9.8) находим
iЭП = 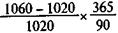
iЭ = 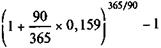
Величину iЭ можно определить и непосредственно по формуле (9.11):
iЭ = 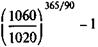
Пример 9.7. Финансовый инструмент, приносящий постоянный процент, куплен за 200 дней до срока его погашения и продан через 100 дней. В момент покупки процентная ставка на рынке была равна 10%, в момент продажи — 9,8%. Доходность операции купли-продажи в виде годовой ставки сложных процентов равна согласно (9.14)
iЭ = 
Пример 9.8. Сертификат с номиналом 100 тыс. руб. с объявленной доходностью 12% годовых (простые проценты) сроком 720 дней куплен за 110 тыс. руб. за 240 дней до его оплаты. Какова доходность инвестиций в виде iЭ?
Если K = 360 дней, то по формуле (9.16) получим
iЭ = 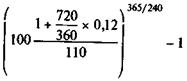
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник